7.2 第1课时平行线的判定 教案(表格式)2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 7.2 第1课时平行线的判定 教案(表格式)2025-2026学年数学北师大版(2024)八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 85.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 00:00:00 | ||
图片预览

文档简介
第1课时 平行线的判定
课标摘录 1.掌握基本事实:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。 2.探索并证明平行线的判定定理:两条直线被第三条直线所截,如果内错角相等(或同旁内角互补),那么这两条直线平行。 3.能用三角板和直尺过已知直线外一点画这条直线的平行线。
素养目标 1.会根据基本事实“同位角相等,两直线平行”来证明“内错角相等,两直线平行”“同旁内角互补,两直线平行”,并能简单应用这些结论。 2.通过画图、讨论、推理等活动,理解和总结证明的步骤、格式和方法。
教学重难点 重点:了解并掌握平行线的判定公理和定理。 难点:灵活应用平行线的三个判定定理解决问题。
教学策略 展示铁轨、双杠等生活实例,让学生观察其特点,引出平行线判定的课题,激发学习兴趣。借助教具演示,如用木条模拟直线位置变化,引导学生总结同位角、内错角、同旁内角的关系与两直线平行的联系,再给出准确判定定理。安排基础证明题与复杂图形题,让学生运用判定定理进行推理,强化对知识的理解和运用。
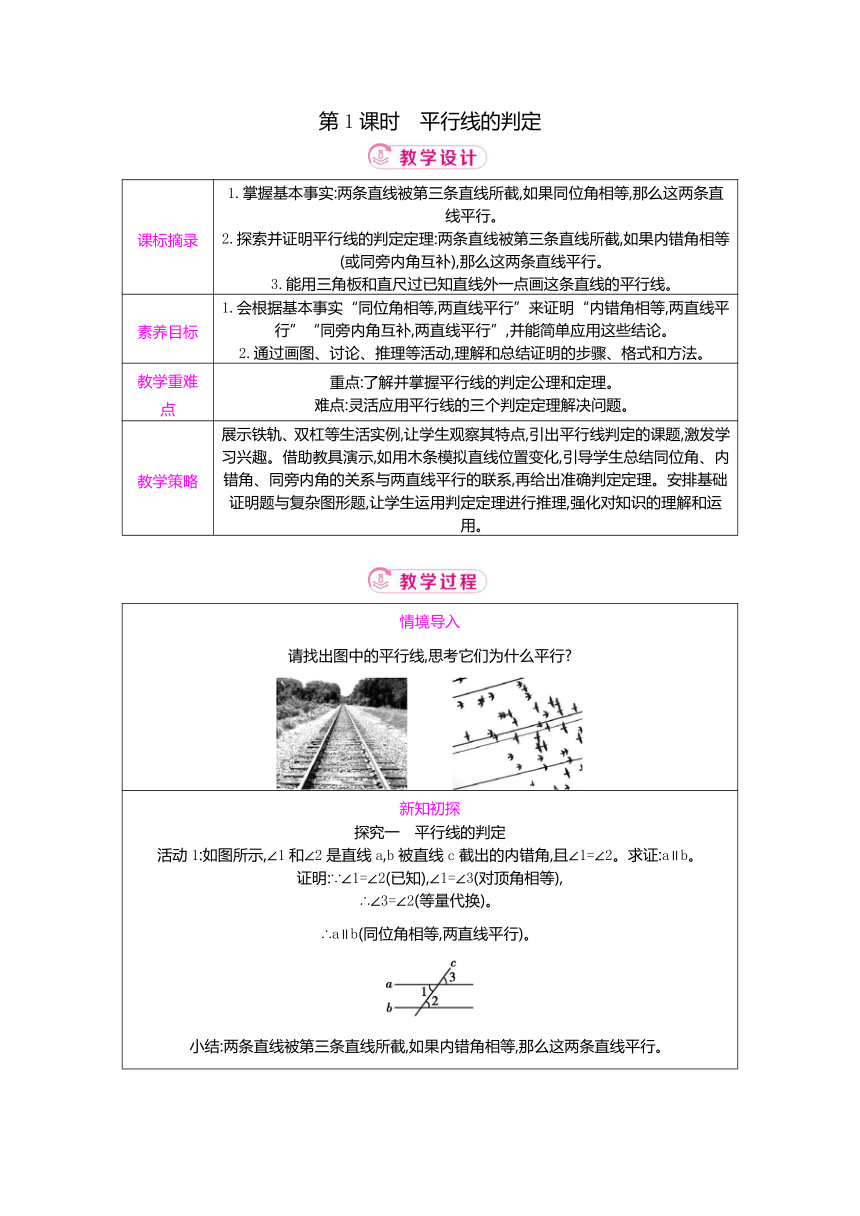
情境导入 请找出图中的平行线,思考它们为什么平行
新知初探 探究一 平行线的判定 活动1:如图所示,∠1和∠2是直线a,b被直线c截出的内错角,且∠1=∠2。求证:a∥b。 证明:∵∠1=∠2(已知),∠1=∠3(对顶角相等), ∴∠3=∠2(等量代换)。 ∴a∥b(同位角相等,两直线平行)。 小结:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。 简述为:内错角相等,两直线平行。 应用格式: ∵∠1=∠2(已知), ∴a∥b(内错角相等,两直线平行)。
活动2:“两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行”这个命题也正确吗 说明理由。 定理证明: 如图所示,∠1和∠2是直线a,b被直线c截出的同旁内角,且∠1与∠2互补。求证:a∥b。 学生思考交流后独立完成,教师给予点评指导。 证明:∵∠1与∠2互补(已知), ∴∠1+∠2=180°(互补的定义)。 ∴∠1=180°-∠2(等式的性质)。 ∵∠3+∠2=180°(平角的定义), ∴∠3=180°-∠2(等式的性质)。 ∴∠1=∠3(等量代换)。 ∴a∥b(同位角相等,两直线平行)。 小结:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。 简述为:同旁内角互补,两直线平行。 应用格式: ∵∠1+∠2=180°(已知), ∴a∥b(同旁内角互补,两直线平行)。 意图说明 两个例子都是以基本事实“同位角相等,两直线平行”为依据分别证明平行线的判定定理:“内错角相等,两直线平行”“同旁内角互补,两直线平行”。在此过程中要引导学生明确现在证明的出发点有哪些,哪些概念、法则、基本事实、定理可用,让学生养成证明时“有理有据”的习惯,培养严谨的学习态度。 探究二 平行线判定的应用 活动3:思考·交流 (1)如图所示,利用两个全等的直角三角尺作出平行线,请说说其中的道理。 解:可以利用“内错角相等,两直线平行”说明两条直线平行。 (2)在一张不规则的四边形纸片上折出平行线,并予以证明;与同伴交流各自的折纸方法与证明过程。 意图说明 利用平行线的判定定理解释作图的道理。教学中还可以让学生利用手中的直尺、三角尺等工具快捷地作出平行线,从而得到更多作平行线的方法,说明道理的方法也可能更为多样,开放教学。
当堂达标
课堂小结
板书设计 平行线的判定 1.平行线的基本事实 2.平行线的判定定理及证明
教学反思
课标摘录 1.掌握基本事实:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。 2.探索并证明平行线的判定定理:两条直线被第三条直线所截,如果内错角相等(或同旁内角互补),那么这两条直线平行。 3.能用三角板和直尺过已知直线外一点画这条直线的平行线。
素养目标 1.会根据基本事实“同位角相等,两直线平行”来证明“内错角相等,两直线平行”“同旁内角互补,两直线平行”,并能简单应用这些结论。 2.通过画图、讨论、推理等活动,理解和总结证明的步骤、格式和方法。
教学重难点 重点:了解并掌握平行线的判定公理和定理。 难点:灵活应用平行线的三个判定定理解决问题。
教学策略 展示铁轨、双杠等生活实例,让学生观察其特点,引出平行线判定的课题,激发学习兴趣。借助教具演示,如用木条模拟直线位置变化,引导学生总结同位角、内错角、同旁内角的关系与两直线平行的联系,再给出准确判定定理。安排基础证明题与复杂图形题,让学生运用判定定理进行推理,强化对知识的理解和运用。
情境导入 请找出图中的平行线,思考它们为什么平行
新知初探 探究一 平行线的判定 活动1:如图所示,∠1和∠2是直线a,b被直线c截出的内错角,且∠1=∠2。求证:a∥b。 证明:∵∠1=∠2(已知),∠1=∠3(对顶角相等), ∴∠3=∠2(等量代换)。 ∴a∥b(同位角相等,两直线平行)。 小结:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。 简述为:内错角相等,两直线平行。 应用格式: ∵∠1=∠2(已知), ∴a∥b(内错角相等,两直线平行)。
活动2:“两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行”这个命题也正确吗 说明理由。 定理证明: 如图所示,∠1和∠2是直线a,b被直线c截出的同旁内角,且∠1与∠2互补。求证:a∥b。 学生思考交流后独立完成,教师给予点评指导。 证明:∵∠1与∠2互补(已知), ∴∠1+∠2=180°(互补的定义)。 ∴∠1=180°-∠2(等式的性质)。 ∵∠3+∠2=180°(平角的定义), ∴∠3=180°-∠2(等式的性质)。 ∴∠1=∠3(等量代换)。 ∴a∥b(同位角相等,两直线平行)。 小结:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。 简述为:同旁内角互补,两直线平行。 应用格式: ∵∠1+∠2=180°(已知), ∴a∥b(同旁内角互补,两直线平行)。 意图说明 两个例子都是以基本事实“同位角相等,两直线平行”为依据分别证明平行线的判定定理:“内错角相等,两直线平行”“同旁内角互补,两直线平行”。在此过程中要引导学生明确现在证明的出发点有哪些,哪些概念、法则、基本事实、定理可用,让学生养成证明时“有理有据”的习惯,培养严谨的学习态度。 探究二 平行线判定的应用 活动3:思考·交流 (1)如图所示,利用两个全等的直角三角尺作出平行线,请说说其中的道理。 解:可以利用“内错角相等,两直线平行”说明两条直线平行。 (2)在一张不规则的四边形纸片上折出平行线,并予以证明;与同伴交流各自的折纸方法与证明过程。 意图说明 利用平行线的判定定理解释作图的道理。教学中还可以让学生利用手中的直尺、三角尺等工具快捷地作出平行线,从而得到更多作平行线的方法,说明道理的方法也可能更为多样,开放教学。
当堂达标
课堂小结
板书设计 平行线的判定 1.平行线的基本事实 2.平行线的判定定理及证明
教学反思
同课章节目录
