2.2.2 函数的奇偶性 课件 (3)
图片预览







文档简介
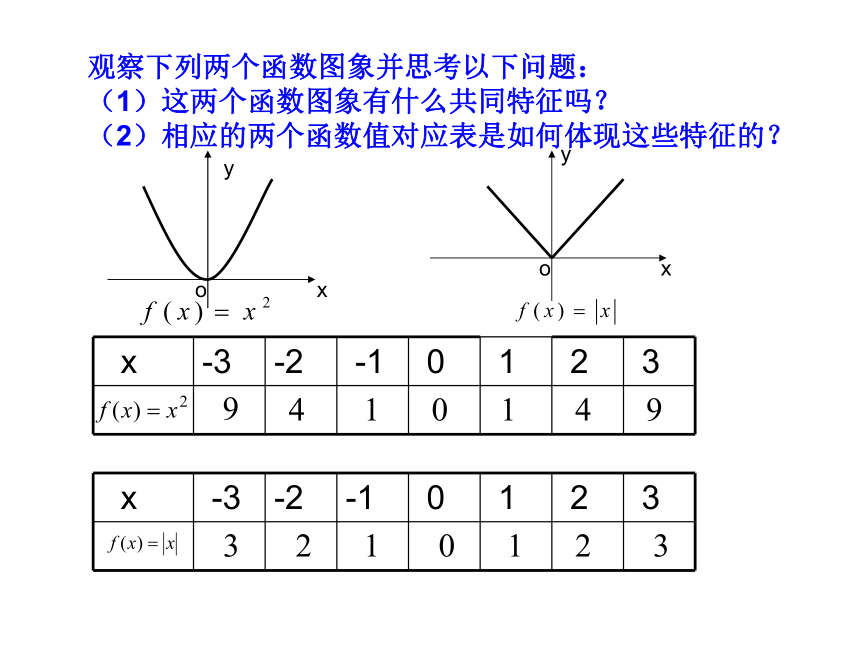
课件22张PPT。第2章 函数2.2.2 函数的奇偶性①②③④xyoxyo 观察下列两个函数图象并思考以下问题:
(1)这两个函数图象有什么共同特征吗?
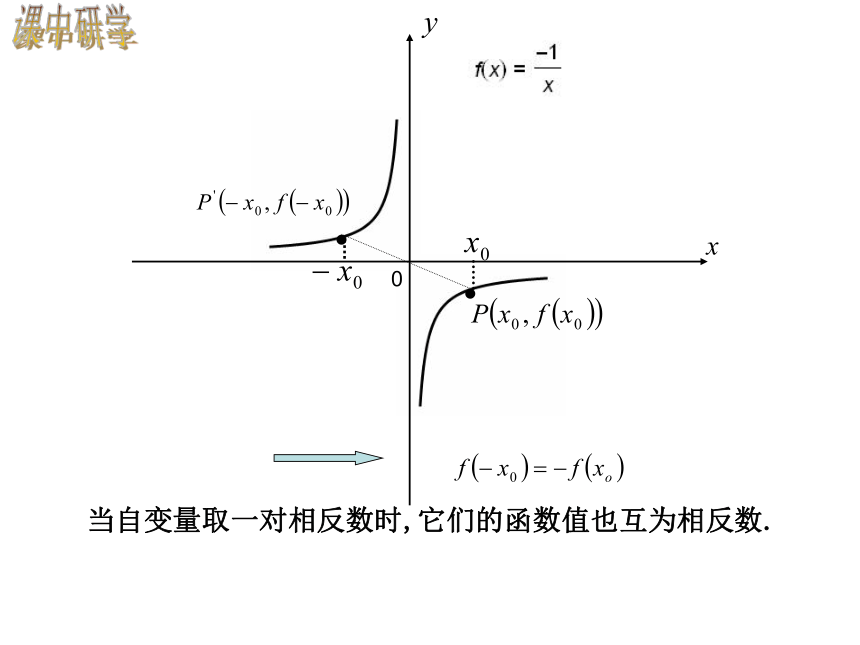
(2)相应的两个函数值对应表是如何体现这些特征的?对于该函数●●当自变量取一对相反数时,它们的函数值相等课中研学定义域中任意一个x,都有f(-x)=f(x)函数图象关于y轴对称对定义域中的任意一个x,都有f(-x)=f(x)数学理论 偶函数的定义 一般的,设函数y=f(x)的定义域为A,如果对于任意的x∈A,都有f(-x)= f(x),那么称函数y=f(x)是偶函数(even fun_ction) 观察函数f(x)=x和f(x)=-1/x的图象(下图),你能发现两个函数图象有什么共同特征吗?f(-3)=-3=-f(3) f(-2)=-2=-f(2) f(-1)=-1=-f(1)f(-3)=1/3=-f(3) f(-2)=1/2=-f(2) f(-1)=1=-f(1)●●0当自变量取一对相反数时,它们的函数值也互为相反数.课中研学 奇函数的定义 一般的,设函数y=f(x)的定义域为A,如果对于任意的x∈A,都有f(-x)= - f(x),那么称函数y=f(x)是奇函数(odd fun_ction )函数图象关于原点对称对定义域中的任
意一个x,都有
f(-x)=-f(x)数学理论(1) 先判断定义域是否关于数“0”对称;若不满足则为非奇非偶函数,若满足则进入(2)
(2) 再判断f(?x)与?f(x)的关系
(3) 下结论:如果对定义域中的任意x都有:f(?x)=f(x)则为偶函数; f(?x)=-f(x)则为奇函数,否则为非奇非偶函数
用定义判断函数奇偶性的步骤:小结:???概念辨析?● 定义:对于f(x)定义域A内的任意一个x,
如果都有f(-x)=-f(x),那么 f(x)为奇函数
如果都有f(-x)=f(x) ,那么 f(x)为偶函数● 图像性质:偶函数的图象关于y轴对称,奇函 数的图象关于原点对称,反之亦然.回顾总结(1) 先判断定义域是否关于数“0”对称;若不满足则为非奇非偶函数,若满足则进入(2)
(2) 再判断f(?x)与?f(x)的关系
(3) 下结论:如果对定义域中的任意x都有:f(?x)=f(x)则为偶函数; f(?x)=-f(x)则为奇函数,否则为非奇非偶函数
●用定义判断函数奇偶性的步骤:●判断函数奇偶性的方法:①图像法,②定义法回顾总结●函数按奇偶性可分为:
①奇函数 ②偶函数
③非奇非偶函数 ④既奇又偶函数●主要思想方法:数形结合,类比推理, 由特殊到一般。回顾总结数量关系形式奇,形数结合论奇偶1.一次函数y=kx+b是奇函数吗?
2.反比例函数是奇函数吗?
3.二次函数一定是定义在R上的偶函数吗?
4.有没有一个函数既是奇函数也是偶函数,探究若奇函数f(x)在x=0处有定义,则f(0)=0是奇函数,求5、如果函数课中探究AC=BCC关于y轴对称的两点横坐标互为相反数,纵坐标相等(a,b)(-a,b)课中研学横坐标互为相反数,纵坐标相等的两点关于y轴对称的(-a,b)(a,b)课中研学关于原点对称的两点横坐标互为相反数,纵坐标也互为相反数。横坐标互为相反数,纵坐标也互为相反数的两点关于原点对称下列函数具有奇偶性吗?课后探究-21
(1)这两个函数图象有什么共同特征吗?
(2)相应的两个函数值对应表是如何体现这些特征的?对于该函数●●当自变量取一对相反数时,它们的函数值相等课中研学定义域中任意一个x,都有f(-x)=f(x)函数图象关于y轴对称对定义域中的任意一个x,都有f(-x)=f(x)数学理论 偶函数的定义 一般的,设函数y=f(x)的定义域为A,如果对于任意的x∈A,都有f(-x)= f(x),那么称函数y=f(x)是偶函数(even fun_ction) 观察函数f(x)=x和f(x)=-1/x的图象(下图),你能发现两个函数图象有什么共同特征吗?f(-3)=-3=-f(3) f(-2)=-2=-f(2) f(-1)=-1=-f(1)f(-3)=1/3=-f(3) f(-2)=1/2=-f(2) f(-1)=1=-f(1)●●0当自变量取一对相反数时,它们的函数值也互为相反数.课中研学 奇函数的定义 一般的,设函数y=f(x)的定义域为A,如果对于任意的x∈A,都有f(-x)= - f(x),那么称函数y=f(x)是奇函数(odd fun_ction )函数图象关于原点对称对定义域中的任
意一个x,都有
f(-x)=-f(x)数学理论(1) 先判断定义域是否关于数“0”对称;若不满足则为非奇非偶函数,若满足则进入(2)
(2) 再判断f(?x)与?f(x)的关系
(3) 下结论:如果对定义域中的任意x都有:f(?x)=f(x)则为偶函数; f(?x)=-f(x)则为奇函数,否则为非奇非偶函数
用定义判断函数奇偶性的步骤:小结:???概念辨析?● 定义:对于f(x)定义域A内的任意一个x,
如果都有f(-x)=-f(x),那么 f(x)为奇函数
如果都有f(-x)=f(x) ,那么 f(x)为偶函数● 图像性质:偶函数的图象关于y轴对称,奇函 数的图象关于原点对称,反之亦然.回顾总结(1) 先判断定义域是否关于数“0”对称;若不满足则为非奇非偶函数,若满足则进入(2)
(2) 再判断f(?x)与?f(x)的关系
(3) 下结论:如果对定义域中的任意x都有:f(?x)=f(x)则为偶函数; f(?x)=-f(x)则为奇函数,否则为非奇非偶函数
●用定义判断函数奇偶性的步骤:●判断函数奇偶性的方法:①图像法,②定义法回顾总结●函数按奇偶性可分为:
①奇函数 ②偶函数
③非奇非偶函数 ④既奇又偶函数●主要思想方法:数形结合,类比推理, 由特殊到一般。回顾总结数量关系形式奇,形数结合论奇偶1.一次函数y=kx+b是奇函数吗?
2.反比例函数是奇函数吗?
3.二次函数一定是定义在R上的偶函数吗?
4.有没有一个函数既是奇函数也是偶函数,探究若奇函数f(x)在x=0处有定义,则f(0)=0是奇函数,求5、如果函数课中探究AC=BCC关于y轴对称的两点横坐标互为相反数,纵坐标相等(a,b)(-a,b)课中研学横坐标互为相反数,纵坐标相等的两点关于y轴对称的(-a,b)(a,b)课中研学关于原点对称的两点横坐标互为相反数,纵坐标也互为相反数。横坐标互为相反数,纵坐标也互为相反数的两点关于原点对称下列函数具有奇偶性吗?课后探究-21
