13.3.1 三角形的内角 第1课时 三角形的内角和定理 学案(含答案)2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 13.3.1 三角形的内角 第1课时 三角形的内角和定理 学案(含答案)2025-2026学年数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 458.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 22:51:02 | ||
图片预览

文档简介
13.3 三角形的内角与外角
13.3.1 三角形的内角
第1课时 三角形的内角和定理
学习目标
1.探索并证明三角形的内角和定理.
2.能运用三角形内角和定理解决简单的与三角形中角有关的计算和证明问题.
自主探索
问题 有一块残缺的三角形木板,量得∠A=100°,∠B=20°,则这块三角形木板的第三个角的度数是多少
任务一 探索并证明三角形的内角和定理
活动1 我们在小学就已经知道,任意一个三角形的内角和等于 180 ,大家回忆一下,当时是怎样知道这个结论的呢?
画出一个三角形,并将它的内角剪下,试着拼拼看.
活动2 (1)在准备的三角形硬纸上标出三角形三个内角的编码,如图1.
问题1 在图2中,直线MN与BC是什么关系
问题2 在图3中,直线CM与AB是什么关系
问题3 你能从中找到三角形内角和定理的证明方法吗
(2)证明三角形内角和定理:三角形三个内角的和等于180 。
归纳总结:
为了证明的需要,在原来的图形上添画的线叫做 线.在平面几何里,辅助线通常画成 线.
【即时测评】
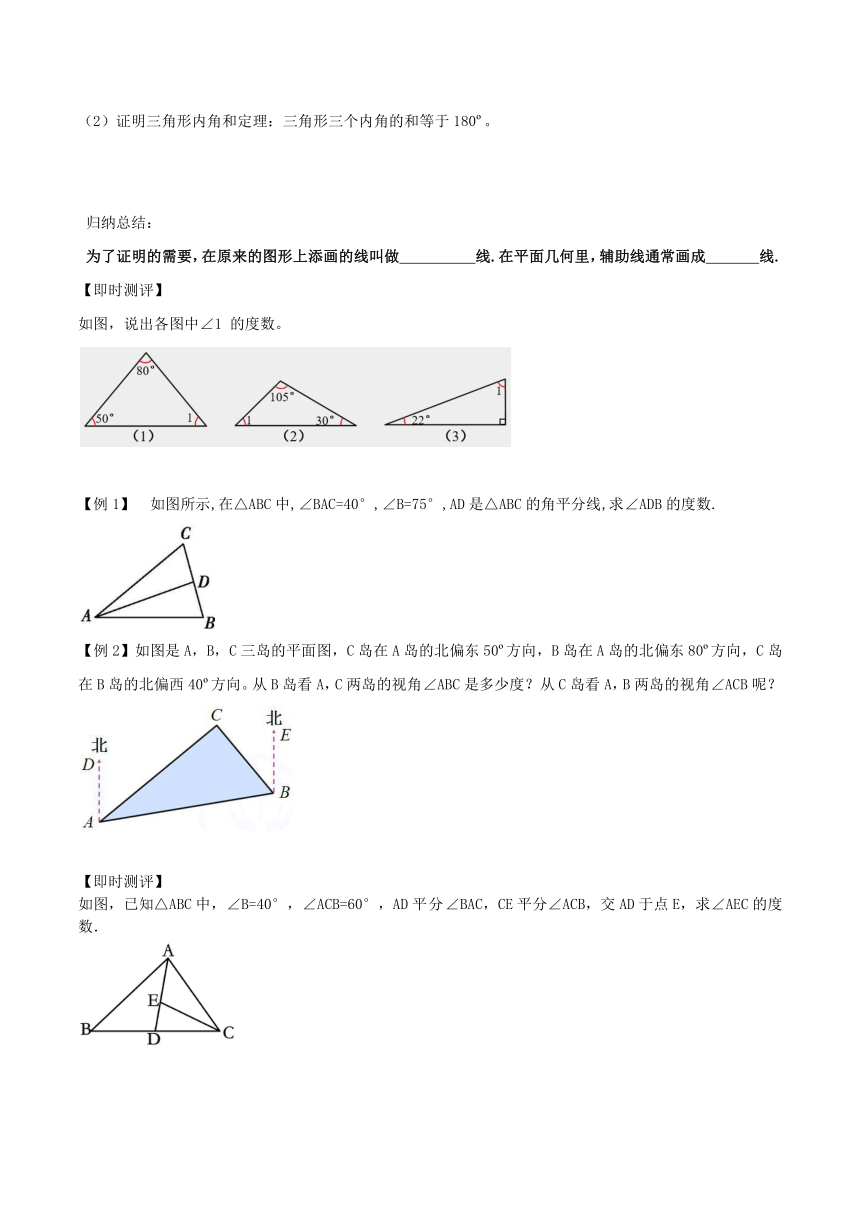
如图,说出各图中∠1 的度数。
【例1】 如图所示,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线,求∠ADB的度数.
【例2】如图是A,B,C三岛的平面图,C岛在A岛的北偏东50 方向,B岛在A岛的北偏东80 方向,C岛在B岛的北偏西40 方向。从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A,B两岛的视角∠ACB呢?
【即时测评】
如图,已知△ABC中,∠B=40°,∠ACB=60°,AD平分∠BAC,CE平分∠ACB,交AD于点E,求∠AEC的度数.
当堂达标
1. 如果一个三角形的两个内角分别是36°和54°,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
2.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
A.85° B.80° C.75° D.70°
3.填空。
(1)在△ABC中,∠A=90°,∠B=65°,则∠C= _____.
(2) 在△ABC中,∠C=42°,∠A=∠B,则∠B=_____.
(3)在△ABC中,∠A=∠B=∠C,则∠A=_____.
(4) 在△ABC中,∠C=30°,∠A:∠B=1:2, 则∠B= _____.
4.如图,已知AD与BC相交于点O,E为CD延长线上的一点,∠B=35°,∠AOB=85°,∠ODE=120°,AB与CD是否平行?为什么?
5.如图,已知:AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
课堂小结
(1)本节课主要学习了哪些知识 学习了哪些数学思想和方法
(2)本节课还有哪些疑惑 请同学们说一说.
参考答案
当堂达标
1.B 2.A 3.25° 69° 60° 100°
4.解:AB∥CD.理由如下:
在△AOB中,∠B=35°,∠AOB=85°,
所以∠A=180°-∠B-∠AOB=60°,
因为∠ODE=120°,
所以∠A+∠ODE=180°,
所以AB∥CD.
5.解:∵AD是△ABC的角平分线,∠BAC=60°,
∴∠BAD=∠DAC=∠BAC=30°,
∵CE是△ABC的高,∠BCE=40°,
∴∠B==90°-40°=50°,
∴∠ADB=180°-∠B-∠BAD=180°-50°-30°=100°.
13.3.1 三角形的内角
第1课时 三角形的内角和定理
学习目标
1.探索并证明三角形的内角和定理.
2.能运用三角形内角和定理解决简单的与三角形中角有关的计算和证明问题.
自主探索
问题 有一块残缺的三角形木板,量得∠A=100°,∠B=20°,则这块三角形木板的第三个角的度数是多少
任务一 探索并证明三角形的内角和定理
活动1 我们在小学就已经知道,任意一个三角形的内角和等于 180 ,大家回忆一下,当时是怎样知道这个结论的呢?
画出一个三角形,并将它的内角剪下,试着拼拼看.
活动2 (1)在准备的三角形硬纸上标出三角形三个内角的编码,如图1.
问题1 在图2中,直线MN与BC是什么关系
问题2 在图3中,直线CM与AB是什么关系
问题3 你能从中找到三角形内角和定理的证明方法吗
(2)证明三角形内角和定理:三角形三个内角的和等于180 。
归纳总结:
为了证明的需要,在原来的图形上添画的线叫做 线.在平面几何里,辅助线通常画成 线.
【即时测评】
如图,说出各图中∠1 的度数。
【例1】 如图所示,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线,求∠ADB的度数.
【例2】如图是A,B,C三岛的平面图,C岛在A岛的北偏东50 方向,B岛在A岛的北偏东80 方向,C岛在B岛的北偏西40 方向。从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A,B两岛的视角∠ACB呢?
【即时测评】
如图,已知△ABC中,∠B=40°,∠ACB=60°,AD平分∠BAC,CE平分∠ACB,交AD于点E,求∠AEC的度数.
当堂达标
1. 如果一个三角形的两个内角分别是36°和54°,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
2.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
A.85° B.80° C.75° D.70°
3.填空。
(1)在△ABC中,∠A=90°,∠B=65°,则∠C= _____.
(2) 在△ABC中,∠C=42°,∠A=∠B,则∠B=_____.
(3)在△ABC中,∠A=∠B=∠C,则∠A=_____.
(4) 在△ABC中,∠C=30°,∠A:∠B=1:2, 则∠B= _____.
4.如图,已知AD与BC相交于点O,E为CD延长线上的一点,∠B=35°,∠AOB=85°,∠ODE=120°,AB与CD是否平行?为什么?
5.如图,已知:AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
课堂小结
(1)本节课主要学习了哪些知识 学习了哪些数学思想和方法
(2)本节课还有哪些疑惑 请同学们说一说.
参考答案
当堂达标
1.B 2.A 3.25° 69° 60° 100°
4.解:AB∥CD.理由如下:
在△AOB中,∠B=35°,∠AOB=85°,
所以∠A=180°-∠B-∠AOB=60°,
因为∠ODE=120°,
所以∠A+∠ODE=180°,
所以AB∥CD.
5.解:∵AD是△ABC的角平分线,∠BAC=60°,
∴∠BAD=∠DAC=∠BAC=30°,
∵CE是△ABC的高,∠BCE=40°,
∴∠B==90°-40°=50°,
∴∠ADB=180°-∠B-∠BAD=180°-50°-30°=100°.
同课章节目录
