14.2 三角形全等的判定 第3课时 SSS 学案(含答案)2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 14.2 三角形全等的判定 第3课时 SSS 学案(含答案)2025-2026学年数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 72.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 22:52:25 | ||
图片预览

文档简介
14.2 三角形全等的判定
第3课时 SSS
学习目标
1.探索并理解“边边边”判定方法,会用“边边边”判定方法证明三角形全等.
2.会用尺规已知三边作三角形,了解作图的道理.
自主探索
1.如图,点B、F、C、E在一条直线上,已知FB=CE,∠B=∠E,请你添加一个适当的条件,使得△ABC≌△DEF.
(1)若添加条件AB=DE,则根据 ,可得△ABC≌△DEF;
(2)若添加条件∠ACB=∠DFE,则根据 ,可得△ABC≌△DEF;
(3)若添加条件∠A=∠D,则根据 ,可得△ABC≌△DEF;
2.前面我们研究了两个三角形符合三个元素对应相等时的哪些情况?还有哪些情况没有研究?
任务一 “边边边”判定方法的探究
活动1 如图,在△A'B'C'与△ABC中,如果A'B'=AB,B'C'=BC,C'A'=CA,那么△A'B'C'≌△ABC,这个判断正确吗
思考 通过以上探究可以得到什么结论?叙述一下.
归纳总结: 分别相等的两个三角形全等(可以简写成“ ”或者“ ”).
你能用符号语言叙述这个基本事实吗?
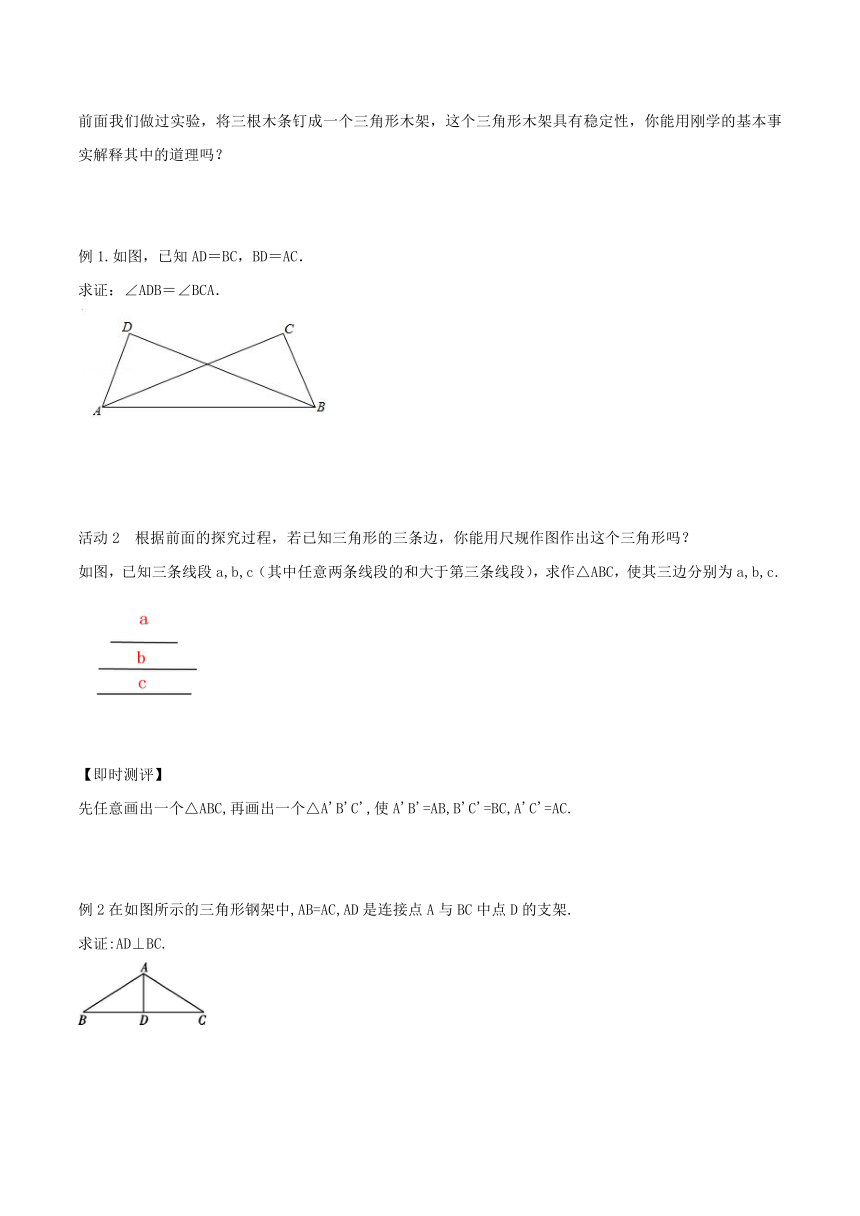
前面我们做过实验,将三根木条钉成一个三角形木架,这个三角形木架具有稳定性,你能用刚学的基本事实解释其中的道理吗?
例1.如图,已知AD=BC,BD=AC.
求证:∠ADB=∠BCA.
活动2 根据前面的探究过程,若已知三角形的三条边,你能用尺规作图作出这个三角形吗?
如图,已知三条线段a,b,c(其中任意两条线段的和大于第三条线段),求作△ABC,使其三边分别为a,b,c.
【即时测评】
先任意画出一个△ABC,再画出一个△A'B'C',使A'B'=AB,B'C'=BC,A'C'=AC.
例2在如图所示的三角形钢架中,AB=AC,AD是连接点A与BC中点D的支架.
求证:AD⊥BC.
问题 三角分别相等的两个三角形全等吗?你能画出三角分别相等但不全等的两个三角形吗?
当堂达标
1. 小明用五根竹棒扎成如图所示的风筝框架,已知AB=CD,AD=CB,下列判断不正确的是( )
(A)∠A=∠C (B)∠ABC=∠CDA(C)∠ABD=∠CDB (D)∠ABD=∠C
2.如图,在四边形ABCD中,AC,BD相交于点O,且AO=BO,DO=CO,AD=BC,则图中全等的三角形有( )
(A)4对 (B)3对 (C)2对 (D)1对
3.如图,已知OA=OB,AC=BC,∠1=30°,则∠ACB的度数是 .
4.已知线段a,请你作出一个等边△ABC,使它的边长等于a.(要求:用尺规作图,不写作法,保留作图痕迹)
5.如图所示,AC=FE,AD=FB,BC=DE.求证:
(1)△ABC≌△FDE;
(2)∠C=∠E.
课堂小结
1.本节课我们主要学习了哪些内容?
2.通过对两个三角形全等条件的进一步探究,你有什么收获?
参考答案
当堂达标
1.D 2.B 3.60°
4.解:如图所示,△ABC即为所求作的三角形.
5.证明:(1)因为AD=FB,所以AD+BD=BF+BD.
所以AB=FD.
在△ABC和△FDE中,
所以△ABC≌△FDE(SSS).
(2)因为△ABC≌△FDE,所以∠C=∠E.
第3课时 SSS
学习目标
1.探索并理解“边边边”判定方法,会用“边边边”判定方法证明三角形全等.
2.会用尺规已知三边作三角形,了解作图的道理.
自主探索
1.如图,点B、F、C、E在一条直线上,已知FB=CE,∠B=∠E,请你添加一个适当的条件,使得△ABC≌△DEF.
(1)若添加条件AB=DE,则根据 ,可得△ABC≌△DEF;
(2)若添加条件∠ACB=∠DFE,则根据 ,可得△ABC≌△DEF;
(3)若添加条件∠A=∠D,则根据 ,可得△ABC≌△DEF;
2.前面我们研究了两个三角形符合三个元素对应相等时的哪些情况?还有哪些情况没有研究?
任务一 “边边边”判定方法的探究
活动1 如图,在△A'B'C'与△ABC中,如果A'B'=AB,B'C'=BC,C'A'=CA,那么△A'B'C'≌△ABC,这个判断正确吗
思考 通过以上探究可以得到什么结论?叙述一下.
归纳总结: 分别相等的两个三角形全等(可以简写成“ ”或者“ ”).
你能用符号语言叙述这个基本事实吗?
前面我们做过实验,将三根木条钉成一个三角形木架,这个三角形木架具有稳定性,你能用刚学的基本事实解释其中的道理吗?
例1.如图,已知AD=BC,BD=AC.
求证:∠ADB=∠BCA.
活动2 根据前面的探究过程,若已知三角形的三条边,你能用尺规作图作出这个三角形吗?
如图,已知三条线段a,b,c(其中任意两条线段的和大于第三条线段),求作△ABC,使其三边分别为a,b,c.
【即时测评】
先任意画出一个△ABC,再画出一个△A'B'C',使A'B'=AB,B'C'=BC,A'C'=AC.
例2在如图所示的三角形钢架中,AB=AC,AD是连接点A与BC中点D的支架.
求证:AD⊥BC.
问题 三角分别相等的两个三角形全等吗?你能画出三角分别相等但不全等的两个三角形吗?
当堂达标
1. 小明用五根竹棒扎成如图所示的风筝框架,已知AB=CD,AD=CB,下列判断不正确的是( )
(A)∠A=∠C (B)∠ABC=∠CDA(C)∠ABD=∠CDB (D)∠ABD=∠C
2.如图,在四边形ABCD中,AC,BD相交于点O,且AO=BO,DO=CO,AD=BC,则图中全等的三角形有( )
(A)4对 (B)3对 (C)2对 (D)1对
3.如图,已知OA=OB,AC=BC,∠1=30°,则∠ACB的度数是 .
4.已知线段a,请你作出一个等边△ABC,使它的边长等于a.(要求:用尺规作图,不写作法,保留作图痕迹)
5.如图所示,AC=FE,AD=FB,BC=DE.求证:
(1)△ABC≌△FDE;
(2)∠C=∠E.
课堂小结
1.本节课我们主要学习了哪些内容?
2.通过对两个三角形全等条件的进一步探究,你有什么收获?
参考答案
当堂达标
1.D 2.B 3.60°
4.解:如图所示,△ABC即为所求作的三角形.
5.证明:(1)因为AD=FB,所以AD+BD=BF+BD.
所以AB=FD.
在△ABC和△FDE中,
所以△ABC≌△FDE(SSS).
(2)因为△ABC≌△FDE,所以∠C=∠E.
同课章节目录
