14.2 三角形全等的判定 第5课时 HL 学案(含答案)2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 14.2 三角形全等的判定 第5课时 HL 学案(含答案)2025-2026学年数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 146.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 22:53:49 | ||
图片预览

文档简介
14.2 三角形全等的判定
第5课时 HL
学习目标
1.探索并理解判定直角三角形全等的“斜边、直角边”定理(“HL”);
2.会用直角三角形全等的判定方法“HL”判定两个直角三角形全等.
自主探索
1.判定三角形全等的方法有哪些
2.如图,已知:Rt△ABC 和 Rt△A′B′C′.
(1)若∠A=∠A′,AB=A′B′,则△ABC与△A′B′C′ (填“全等”或“不全等”),根据 (用简写法).
(2)若AC=A′C′,BC=B′C′,则△ABC与△A′B′C′ (填“全等”或 “不全等”),根据 (用简写法).
3.如图所示,舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.你能帮工作人员想个办法吗
任务一 探究“斜边、直角边”定理
活动1 如图,已知Rt△ABC 和 Rt△A′B′C′,若BC=B′C′,AB=A′B′,那么△ABC与△A′B′C′全等吗?
问题1 如果使点C与点C'重合,并且使射线C'A'与射线CA重合,那么点B与点B'重合吗?为什么?
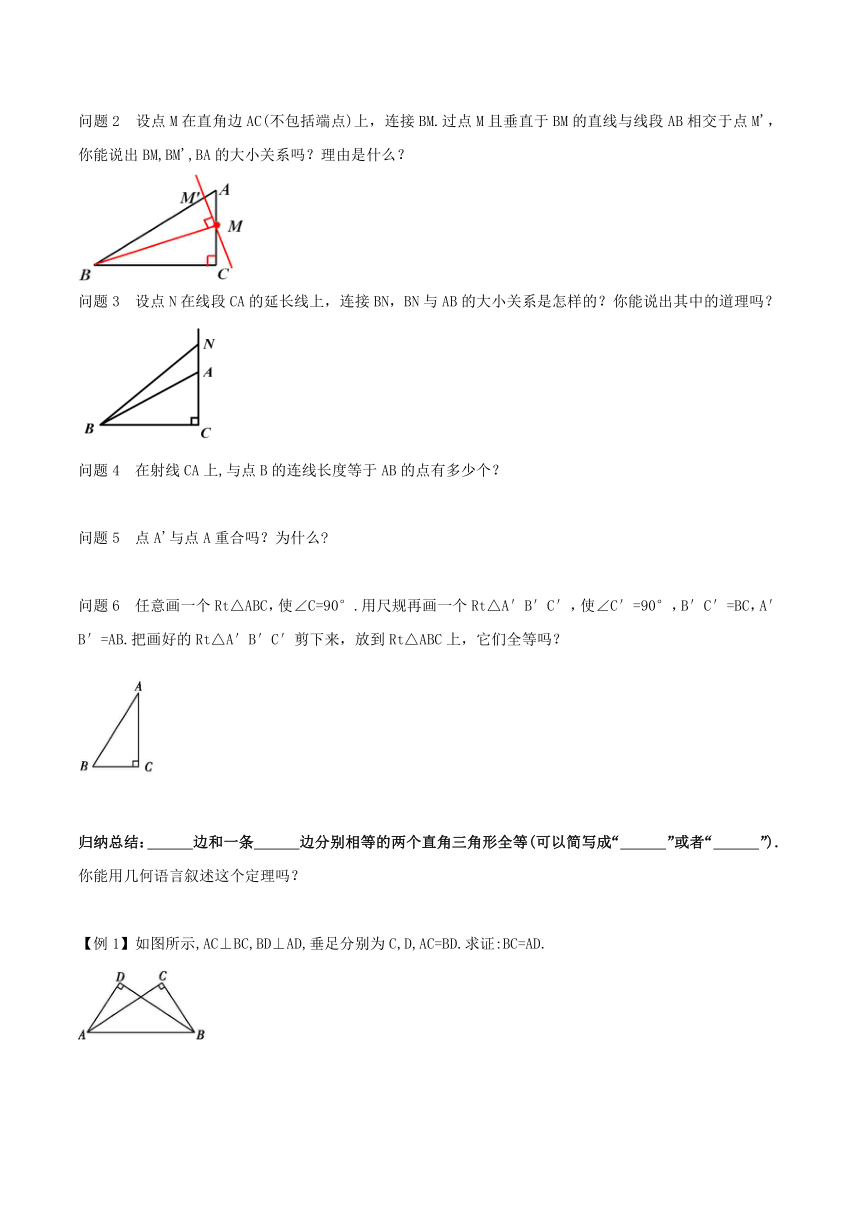
问题2 设点M在直角边AC(不包括端点)上,连接BM.过点M且垂直于BM的直线与线段AB相交于点M',你能说出BM,BM',BA的大小关系吗?理由是什么?
问题3 设点N在线段CA的延长线上,连接BN,BN与AB的大小关系是怎样的?你能说出其中的道理吗?
问题4 在射线CA上,与点B的连线长度等于AB的点有多少个?
问题5 点A'与点A重合吗?为什么
问题6 任意画一个Rt△ABC,使∠C=90°.用尺规再画一个Rt△A′B′C′,使∠C′=90°,B′C′=BC,A′B′=AB.把画好的Rt△A′B′C′剪下来,放到Rt△ABC上,它们全等吗?
归纳总结: 边和一条 边分别相等的两个直角三角形全等(可以简写成“ ”或者“ ”).
你能用几何语言叙述这个定理吗?
【例1】如图所示,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.求证:BC=AD.
任务二 直角三角形的判定方法
活动1 判定两个直角三角形全等有哪些方法?
已知条件 可选择的判定方法 需寻找的条件
一锐角对应相等
斜边对应相等
一直角边对应相等
例2 如图所示,在Rt△ABC和Rt△A'B'C'中,∠B=∠B'=90°,有如下几个条件:①AC=A'C',∠A=∠A';②AC=A'C',AB=A'B';③AC=A'C',BC=B'C';④AB=A'B',∠A=∠A'.其中能判定Rt△ABC≌Rt△A'B'C'的条件有( )
A.1个 B.2个 C.3个 D.4个
【即时测评】
如图,AB=CD,AE⊥BC,DF⊥BC,垂足分别为E,F,CE=BF,下列结论错误的是( )
A.∠C=∠B B.CD∥AB C.∠A+∠D=90° D.CF=BE
当堂达标
1. 判断两个直角三角形全等的方法不正确的有( )
A.两条直角边对应相等 B.斜边和一锐角对应相等
C.斜边和一条直角边对应相等 D.两个锐角对应相等
2.如图,已知AC⊥AB,AC⊥CD,要使得△ABC≌△CDA.
(1)若以“SAS”为依据,需添加条件 .
(2)若以“HL”为依据,需添加条件 .
3.如图,小明和小芳以相同的速度分别同时从A,B出发,小明沿AC行走,小芳沿BD行走,并同时到达C,D.若CB⊥AB,DA⊥AB,则CB与DA相等吗 为什么
4.如图所示,B,E,F,C在同一直线上,AF⊥BC于点F,DE⊥BC于点E,AB=DC,BE=CF,你认为AB平行于CD吗 说说你的理由.
课堂小结
1.本节课你学习了哪些新知识?有哪些体会和收获?
2.在做题过程中你出现了哪些错误?错因是什么?
3.本节课你还有哪些疑惑?
参考答案
当堂达标
1.D 2.AB=CD BC=AD
3.解:CB=DA.
理由:由题意易知AC=BD,
∵CB⊥AB,DA⊥AB,
∴∠DAB=∠CBA=90°,
在Rt△DAB和Rt△CBA中,
∴Rt△DAB≌Rt△CBA(HL).
∴DA=CB.
4.解:平行.理由如下:
因为AF⊥BC,DE⊥BC,
所以∠AFB=∠DEC=90°.
又BE=CF,
所以BE+EF=CF+EF,
即BF=CE.
在Rt△ABF和Rt△DCE中,
所以Rt△ABF≌Rt△DCE(HL).
所以∠B=∠C.
所以AB∥CD.
第5课时 HL
学习目标
1.探索并理解判定直角三角形全等的“斜边、直角边”定理(“HL”);
2.会用直角三角形全等的判定方法“HL”判定两个直角三角形全等.
自主探索
1.判定三角形全等的方法有哪些
2.如图,已知:Rt△ABC 和 Rt△A′B′C′.
(1)若∠A=∠A′,AB=A′B′,则△ABC与△A′B′C′ (填“全等”或“不全等”),根据 (用简写法).
(2)若AC=A′C′,BC=B′C′,则△ABC与△A′B′C′ (填“全等”或 “不全等”),根据 (用简写法).
3.如图所示,舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.你能帮工作人员想个办法吗
任务一 探究“斜边、直角边”定理
活动1 如图,已知Rt△ABC 和 Rt△A′B′C′,若BC=B′C′,AB=A′B′,那么△ABC与△A′B′C′全等吗?
问题1 如果使点C与点C'重合,并且使射线C'A'与射线CA重合,那么点B与点B'重合吗?为什么?
问题2 设点M在直角边AC(不包括端点)上,连接BM.过点M且垂直于BM的直线与线段AB相交于点M',你能说出BM,BM',BA的大小关系吗?理由是什么?
问题3 设点N在线段CA的延长线上,连接BN,BN与AB的大小关系是怎样的?你能说出其中的道理吗?
问题4 在射线CA上,与点B的连线长度等于AB的点有多少个?
问题5 点A'与点A重合吗?为什么
问题6 任意画一个Rt△ABC,使∠C=90°.用尺规再画一个Rt△A′B′C′,使∠C′=90°,B′C′=BC,A′B′=AB.把画好的Rt△A′B′C′剪下来,放到Rt△ABC上,它们全等吗?
归纳总结: 边和一条 边分别相等的两个直角三角形全等(可以简写成“ ”或者“ ”).
你能用几何语言叙述这个定理吗?
【例1】如图所示,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.求证:BC=AD.
任务二 直角三角形的判定方法
活动1 判定两个直角三角形全等有哪些方法?
已知条件 可选择的判定方法 需寻找的条件
一锐角对应相等
斜边对应相等
一直角边对应相等
例2 如图所示,在Rt△ABC和Rt△A'B'C'中,∠B=∠B'=90°,有如下几个条件:①AC=A'C',∠A=∠A';②AC=A'C',AB=A'B';③AC=A'C',BC=B'C';④AB=A'B',∠A=∠A'.其中能判定Rt△ABC≌Rt△A'B'C'的条件有( )
A.1个 B.2个 C.3个 D.4个
【即时测评】
如图,AB=CD,AE⊥BC,DF⊥BC,垂足分别为E,F,CE=BF,下列结论错误的是( )
A.∠C=∠B B.CD∥AB C.∠A+∠D=90° D.CF=BE
当堂达标
1. 判断两个直角三角形全等的方法不正确的有( )
A.两条直角边对应相等 B.斜边和一锐角对应相等
C.斜边和一条直角边对应相等 D.两个锐角对应相等
2.如图,已知AC⊥AB,AC⊥CD,要使得△ABC≌△CDA.
(1)若以“SAS”为依据,需添加条件 .
(2)若以“HL”为依据,需添加条件 .
3.如图,小明和小芳以相同的速度分别同时从A,B出发,小明沿AC行走,小芳沿BD行走,并同时到达C,D.若CB⊥AB,DA⊥AB,则CB与DA相等吗 为什么
4.如图所示,B,E,F,C在同一直线上,AF⊥BC于点F,DE⊥BC于点E,AB=DC,BE=CF,你认为AB平行于CD吗 说说你的理由.
课堂小结
1.本节课你学习了哪些新知识?有哪些体会和收获?
2.在做题过程中你出现了哪些错误?错因是什么?
3.本节课你还有哪些疑惑?
参考答案
当堂达标
1.D 2.AB=CD BC=AD
3.解:CB=DA.
理由:由题意易知AC=BD,
∵CB⊥AB,DA⊥AB,
∴∠DAB=∠CBA=90°,
在Rt△DAB和Rt△CBA中,
∴Rt△DAB≌Rt△CBA(HL).
∴DA=CB.
4.解:平行.理由如下:
因为AF⊥BC,DE⊥BC,
所以∠AFB=∠DEC=90°.
又BE=CF,
所以BE+EF=CF+EF,
即BF=CE.
在Rt△ABF和Rt△DCE中,
所以Rt△ABF≌Rt△DCE(HL).
所以∠B=∠C.
所以AB∥CD.
同课章节目录
