15.1.2 线段的垂直平分线 第1课时 线段垂直平分线的性质与判定 学案(含答案)2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 15.1.2 线段的垂直平分线 第1课时 线段垂直平分线的性质与判定 学案(含答案)2025-2026学年数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 107.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 22:56:05 | ||
图片预览

文档简介
15.1.2 线段的垂直平分线
第1课时 线段垂直平分线的性质与判定
学习目标
1.探究并掌握线段垂直平分线的性质和判定.
2.能运用线段垂直平分线的性质和判定解决简单的计算与推理问题.
3.理解互逆命题和互逆定理的相关概念.
自主探索
复习回顾:
1.轴对称有什么性质?
2.线段是轴对称图形吗?它的对称轴是什么?
3.什么叫线段的垂直平分线?
任务一 探究线段垂直平分线的性质与判定
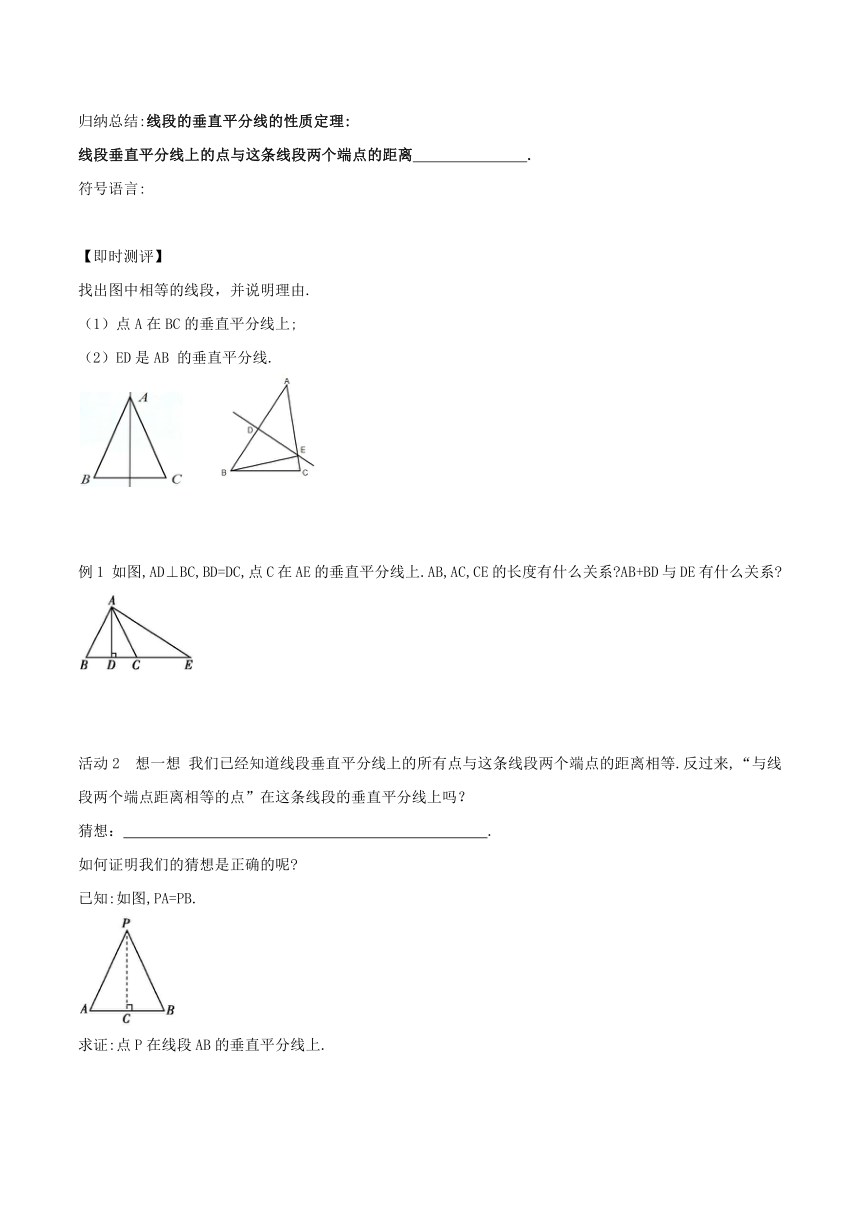
活动1 直线l垂直平分线段AB, P1、P2、P3…是l上的点,分别量一量点P1、P2、P3…到点A与点B的距离,你有什么发现?
发现:
你能猜想得到什么结论?
【猜想】 .
【验证】如图所示,直线l⊥AB,垂足为C,AC=CB,点P在l上.求证:PA=PB.
归纳总结:线段的垂直平分线的性质定理:
线段垂直平分线上的点与这条线段两个端点的距离 .
符号语言:
【即时测评】
找出图中相等的线段,并说明理由.
(1)点A在BC的垂直平分线上;
(2)ED是AB 的垂直平分线.
例1 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.AB,AC,CE的长度有什么关系 AB+BD与DE有什么关系
活动2 想一想 我们已经知道线段垂直平分线上的所有点与这条线段两个端点的距离相等.反过来,“与线段两个端点距离相等的点”在这条线段的垂直平分线上吗?
猜想: .
如何证明我们的猜想是正确的呢
已知:如图,PA=PB.
求证:点P在线段AB的垂直平分线上.
归纳总结:
线段垂直平分线的判定: 的点在这条线段的垂直平分线上.
符号语言:
例2 如图所示,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗
任务二 逆命题与逆定理
活动1 思考 分析上面关于线段的垂直平分线的两个命题,它们的题设和结论有什么关系?你还学习过其他具有类似关系的命题吗?
归纳总结:这两个命题的题设、结论正好相反,我们把具有这种关系的两个命题叫作 命题,如果把其中一个叫作原命题,那么另一个叫作它的 命题.
问题1 写出下列各命题的逆命题,这些逆命题成立吗?
(1)同旁内角互补,两直线平行;
(2)对顶角相等;
(3)全等三角形的对应边相等;
(4)如果两个实数相等,那么它们的平方相等.
归纳总结:一般地,原命题成立时,它的逆命题 ,
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫作 ,其中一个定理叫作另一个定理的 .
问题2 你能举出几个互逆定理的例子吗.
【即时测评】
下列说法正确的是( )
A.命题一定有逆命题 B.所有的定理一定有逆定理
C.真命题的逆命题一定是真命题 D.假命题的逆命题一定是假命题
当堂达标
1.如图所示,AC=AD,BC=BD,则下列说法正确的是( )
A.AB垂直平分CD B.CD垂直平分AB C.AB与CD互相垂直平分 D.CD平分∠ACB
第1题图 第3题图 第4题图
2.到三角形三个顶点的距离相等的点是( )
A.三条角平分线的交点 B.三边垂直平分线的交点 C.三边高线的交点 D.没有这样的点
3.如图,已知在△ABC中,DE是BC的垂直平分线,垂足为E,交AC于点D,若AB=6,AC=9,则△ABD的周长是 .
4.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.若AB=5cm,BC=6cm,则AC= ,DE= .
5.如图所示,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.求证:OE是CD的垂直平分线.
6.写出下列命题的逆命题,并判断其真假,指出其中的互逆定理.
(1)三边对应相等的两个三角形全等;
(2)全等三角形的三个角对应相等;
(3)两直线平行,同旁内角互补.
课堂小结
1.本节课你学习了哪些新知识?有哪些体会和收获?
2.在做题过程中你出现了哪些错误?错因是什么?
3.本节课你还有哪些疑惑?
参考答案
当堂达标
1.A 2.B 3.15 4.5cm 8cm
5.证明:因为OE平分∠AOB,EC⊥OA,ED⊥OB,
所以DE=CE.
因为点E是∠AOB的平分线上一点,
所以∠DOE=∠COE,
因为EC⊥OA,ED⊥OB,所以∠ODE=∠OCE=90°,
所以△OED≌△OEC(AAS),所以OC=OD;
所以 OE是CD的垂直平分线.
6.解:(1)逆命题是全等三角形的三边对应相等,真命题,是互逆定理.
(2)逆命题是三个角对应相等的两个三角形全等,假命题.
(4)逆命题是同旁内角互补,两直线平行,真命题,是互逆定理.
第1课时 线段垂直平分线的性质与判定
学习目标
1.探究并掌握线段垂直平分线的性质和判定.
2.能运用线段垂直平分线的性质和判定解决简单的计算与推理问题.
3.理解互逆命题和互逆定理的相关概念.
自主探索
复习回顾:
1.轴对称有什么性质?
2.线段是轴对称图形吗?它的对称轴是什么?
3.什么叫线段的垂直平分线?
任务一 探究线段垂直平分线的性质与判定
活动1 直线l垂直平分线段AB, P1、P2、P3…是l上的点,分别量一量点P1、P2、P3…到点A与点B的距离,你有什么发现?
发现:
你能猜想得到什么结论?
【猜想】 .
【验证】如图所示,直线l⊥AB,垂足为C,AC=CB,点P在l上.求证:PA=PB.
归纳总结:线段的垂直平分线的性质定理:
线段垂直平分线上的点与这条线段两个端点的距离 .
符号语言:
【即时测评】
找出图中相等的线段,并说明理由.
(1)点A在BC的垂直平分线上;
(2)ED是AB 的垂直平分线.
例1 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.AB,AC,CE的长度有什么关系 AB+BD与DE有什么关系
活动2 想一想 我们已经知道线段垂直平分线上的所有点与这条线段两个端点的距离相等.反过来,“与线段两个端点距离相等的点”在这条线段的垂直平分线上吗?
猜想: .
如何证明我们的猜想是正确的呢
已知:如图,PA=PB.
求证:点P在线段AB的垂直平分线上.
归纳总结:
线段垂直平分线的判定: 的点在这条线段的垂直平分线上.
符号语言:
例2 如图所示,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗
任务二 逆命题与逆定理
活动1 思考 分析上面关于线段的垂直平分线的两个命题,它们的题设和结论有什么关系?你还学习过其他具有类似关系的命题吗?
归纳总结:这两个命题的题设、结论正好相反,我们把具有这种关系的两个命题叫作 命题,如果把其中一个叫作原命题,那么另一个叫作它的 命题.
问题1 写出下列各命题的逆命题,这些逆命题成立吗?
(1)同旁内角互补,两直线平行;
(2)对顶角相等;
(3)全等三角形的对应边相等;
(4)如果两个实数相等,那么它们的平方相等.
归纳总结:一般地,原命题成立时,它的逆命题 ,
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理叫作 ,其中一个定理叫作另一个定理的 .
问题2 你能举出几个互逆定理的例子吗.
【即时测评】
下列说法正确的是( )
A.命题一定有逆命题 B.所有的定理一定有逆定理
C.真命题的逆命题一定是真命题 D.假命题的逆命题一定是假命题
当堂达标
1.如图所示,AC=AD,BC=BD,则下列说法正确的是( )
A.AB垂直平分CD B.CD垂直平分AB C.AB与CD互相垂直平分 D.CD平分∠ACB
第1题图 第3题图 第4题图
2.到三角形三个顶点的距离相等的点是( )
A.三条角平分线的交点 B.三边垂直平分线的交点 C.三边高线的交点 D.没有这样的点
3.如图,已知在△ABC中,DE是BC的垂直平分线,垂足为E,交AC于点D,若AB=6,AC=9,则△ABD的周长是 .
4.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.若AB=5cm,BC=6cm,则AC= ,DE= .
5.如图所示,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.求证:OE是CD的垂直平分线.
6.写出下列命题的逆命题,并判断其真假,指出其中的互逆定理.
(1)三边对应相等的两个三角形全等;
(2)全等三角形的三个角对应相等;
(3)两直线平行,同旁内角互补.
课堂小结
1.本节课你学习了哪些新知识?有哪些体会和收获?
2.在做题过程中你出现了哪些错误?错因是什么?
3.本节课你还有哪些疑惑?
参考答案
当堂达标
1.A 2.B 3.15 4.5cm 8cm
5.证明:因为OE平分∠AOB,EC⊥OA,ED⊥OB,
所以DE=CE.
因为点E是∠AOB的平分线上一点,
所以∠DOE=∠COE,
因为EC⊥OA,ED⊥OB,所以∠ODE=∠OCE=90°,
所以△OED≌△OEC(AAS),所以OC=OD;
所以 OE是CD的垂直平分线.
6.解:(1)逆命题是全等三角形的三边对应相等,真命题,是互逆定理.
(2)逆命题是三个角对应相等的两个三角形全等,假命题.
(4)逆命题是同旁内角互补,两直线平行,真命题,是互逆定理.
同课章节目录
