15.3.1 等腰三角形 第1课时 等腰三角形的性质 学案(含答案)2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 15.3.1 等腰三角形 第1课时 等腰三角形的性质 学案(含答案)2025-2026学年数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 45.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 22:57:51 | ||
图片预览

文档简介
15.3 等腰三角形
15.3.1 等腰三角形
第1课时 等腰三角形的性质
学习目标
1.经历探究等腰三角形的性质的过程,培养观察、分析、归纳和合情推理的能力;
2.掌握等腰三角形的性质,会用等腰三角形的性质解决有关问题.
自主探索
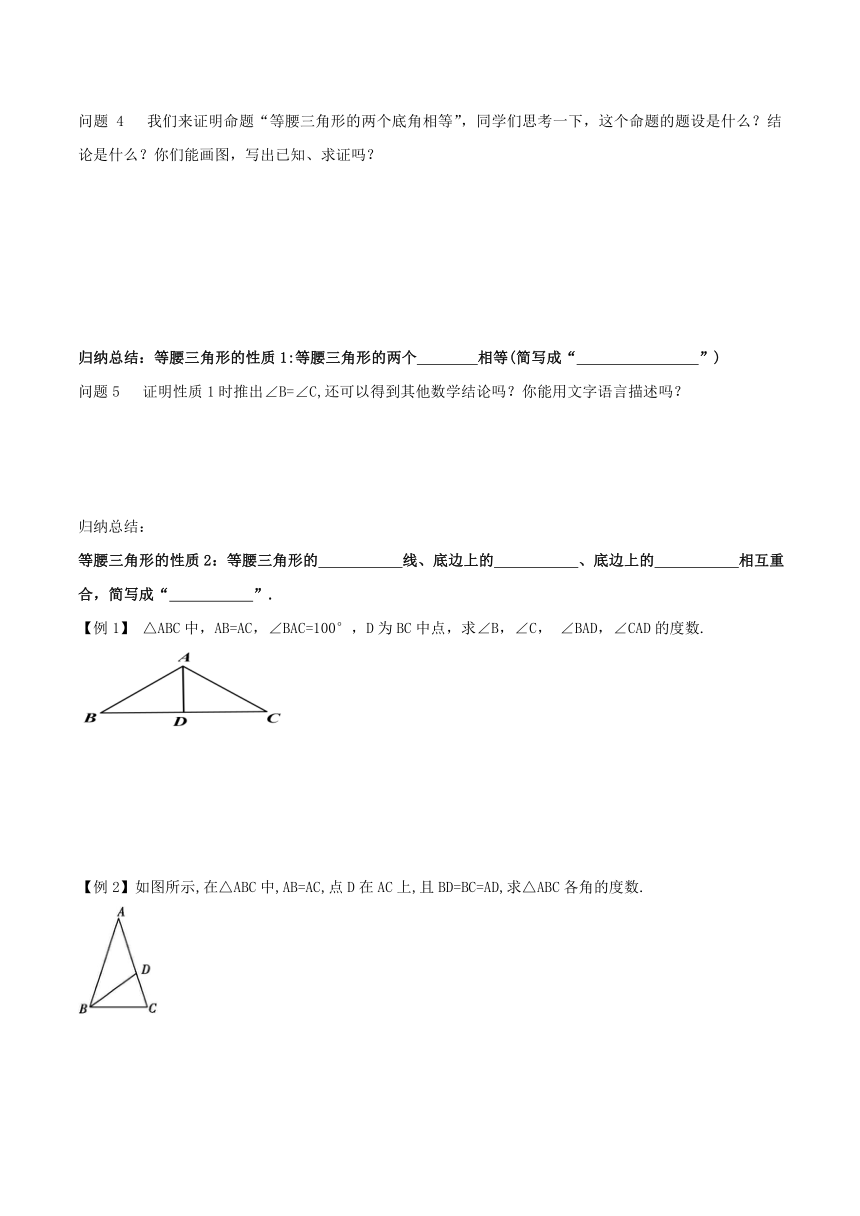
如图,把一张长方形纸沿图中虚线对折,并剪下阴影部分,再把它展开铺平,得到的三角形是什么特殊三角形 它具有哪些性质
任务一 探究等腰三角形的性质
思考
(1) 什么样的三角形为等腰三角形?
(2) 一般的三角形与等腰三角形在角上有什么不同?等腰三角形特殊在哪里?
活动1 如图,在纸上画一个等腰三角形,把它剪下来.
问题1 等腰三角形是轴对称图形吗?它有几条对称轴
问题2 将这个剪下的等腰三角形对折,使它的两腰重合,再展开,找出其中重合的线段与角.
问题3 由这些重合的线段和角,你能发现等腰三角形的性质吗?说一说你的猜想.
问题 4 我们来证明命题“等腰三角形的两个底角相等”,同学们思考一下,这个命题的题设是什么?结论是什么?你们能画图,写出已知、求证吗?
归纳总结:等腰三角形的性质1:等腰三角形的两个 相等(简写成“ ”)
问题5 证明性质1时推出∠B=∠C,还可以得到其他数学结论吗?你能用文字语言描述吗?
归纳总结:
等腰三角形的性质2:等腰三角形的 线、底边上的 、底边上的 相互重合,简写成“ ”.
【例1】 △ABC中,AB=AC,∠BAC=100°,D为BC中点,求∠B,∠C, ∠BAD,∠CAD的度数.
【例2】如图所示,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
当堂达标
1.判断正误:
(1)等腰三角形的顶角一定是锐角( ) .
(2)等腰三角形的底角可能是锐角或者直角、钝角都可以( ).
(3)钝角三角形不可能是等腰三角形( ).
(4)等腰三角形的顶角平分线一定垂直底边( ).
(5)等腰三角形的角平分线、中线和高互相重合( ).
(6)等腰三角形底边上的中线一定平分顶角( ).
2.在等腰三角形ABC中,AB=AC,∠A=30°,则∠B等于( )
A.30° B.60° C.75° D.85°
3.等腰三角形的一个外角是100°,它的顶角的度数是( )
A.80° B.20°C.20°或80° D.50°或80°
4.如图所示,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于( )
A.10 B.5 C.4 D.3
第4题图 第5题图
5.如图所示,在△ABC中,已知AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为( )
A.35° B.45° C.55° D.60°
6.如图所示,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
课堂小结
1.本节课学习了什么内容?
2.为什么研究等腰三角形?如何研究等腰三角形?
参考答案
当堂达标
1.× × × √ × √ 2.C 3.C 4.B 5.C
6.解:因为∠BAD=26°,AB=AD,
所以∠B=∠ADB=×(180°-26°)=77°.
因为AD=CD,所以∠C=∠DAC.
因为∠ADB=∠C+∠DAC=2∠C,
所以∠C=∠ADB=38.5°.
15.3.1 等腰三角形
第1课时 等腰三角形的性质
学习目标
1.经历探究等腰三角形的性质的过程,培养观察、分析、归纳和合情推理的能力;
2.掌握等腰三角形的性质,会用等腰三角形的性质解决有关问题.
自主探索
如图,把一张长方形纸沿图中虚线对折,并剪下阴影部分,再把它展开铺平,得到的三角形是什么特殊三角形 它具有哪些性质
任务一 探究等腰三角形的性质
思考
(1) 什么样的三角形为等腰三角形?
(2) 一般的三角形与等腰三角形在角上有什么不同?等腰三角形特殊在哪里?
活动1 如图,在纸上画一个等腰三角形,把它剪下来.
问题1 等腰三角形是轴对称图形吗?它有几条对称轴
问题2 将这个剪下的等腰三角形对折,使它的两腰重合,再展开,找出其中重合的线段与角.
问题3 由这些重合的线段和角,你能发现等腰三角形的性质吗?说一说你的猜想.
问题 4 我们来证明命题“等腰三角形的两个底角相等”,同学们思考一下,这个命题的题设是什么?结论是什么?你们能画图,写出已知、求证吗?
归纳总结:等腰三角形的性质1:等腰三角形的两个 相等(简写成“ ”)
问题5 证明性质1时推出∠B=∠C,还可以得到其他数学结论吗?你能用文字语言描述吗?
归纳总结:
等腰三角形的性质2:等腰三角形的 线、底边上的 、底边上的 相互重合,简写成“ ”.
【例1】 △ABC中,AB=AC,∠BAC=100°,D为BC中点,求∠B,∠C, ∠BAD,∠CAD的度数.
【例2】如图所示,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
当堂达标
1.判断正误:
(1)等腰三角形的顶角一定是锐角( ) .
(2)等腰三角形的底角可能是锐角或者直角、钝角都可以( ).
(3)钝角三角形不可能是等腰三角形( ).
(4)等腰三角形的顶角平分线一定垂直底边( ).
(5)等腰三角形的角平分线、中线和高互相重合( ).
(6)等腰三角形底边上的中线一定平分顶角( ).
2.在等腰三角形ABC中,AB=AC,∠A=30°,则∠B等于( )
A.30° B.60° C.75° D.85°
3.等腰三角形的一个外角是100°,它的顶角的度数是( )
A.80° B.20°C.20°或80° D.50°或80°
4.如图所示,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于( )
A.10 B.5 C.4 D.3
第4题图 第5题图
5.如图所示,在△ABC中,已知AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为( )
A.35° B.45° C.55° D.60°
6.如图所示,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
课堂小结
1.本节课学习了什么内容?
2.为什么研究等腰三角形?如何研究等腰三角形?
参考答案
当堂达标
1.× × × √ × √ 2.C 3.C 4.B 5.C
6.解:因为∠BAD=26°,AB=AD,
所以∠B=∠ADB=×(180°-26°)=77°.
因为AD=CD,所以∠C=∠DAC.
因为∠ADB=∠C+∠DAC=2∠C,
所以∠C=∠ADB=38.5°.
同课章节目录
