15.3.2 等边三角形 第1课时 等边三角形的性质与判定 学案(含答案)2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 15.3.2 等边三角形 第1课时 等边三角形的性质与判定 学案(含答案)2025-2026学年数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 116.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 22:58:43 | ||
图片预览

文档简介
15.3.2 等边三角形
第1课时 等边三角形的性质与判定
学习目标
1.会阐述、推证等边三角形的性质和判定,掌握等边三角形的性质定理和判定定理.
2.在观察、猜想、证明等边三角形性质和判定的过程中,发展合情推理能力和演绎推理能力.
3.能运用等边三角形的性质和判定进行计算和证明,培养推理和运算能力及应用意识.
自主探索
1.等腰三角形有哪些性质和判定方法?
2.三角形怎样按边进行分类?
任务一 探究等边三角形的性质
问题 你能说出等边三角形的定义并结合图形写出符号语言吗
活动1 类比探究等边三角形的性质
问题 等腰三角形有哪些性质?
根据等边三角形与等腰三角形的关系,说出等边三角形有哪些性质?
如图所示,已知△ABC是等边三角形,求证:∠A=∠B=∠C.
归纳总结:等边三角形的三个内角都 ,并且每个角都等于 .
符号语言:
问题 你能运用类比的方法探索等腰三角形与等边三角形的联系与区别吗
类比归纳:等腰三角形和等边三角形的性质
等腰三角形的性质 等边三角形的性质
边
角
“三线合一”
对称性
【即时测评】
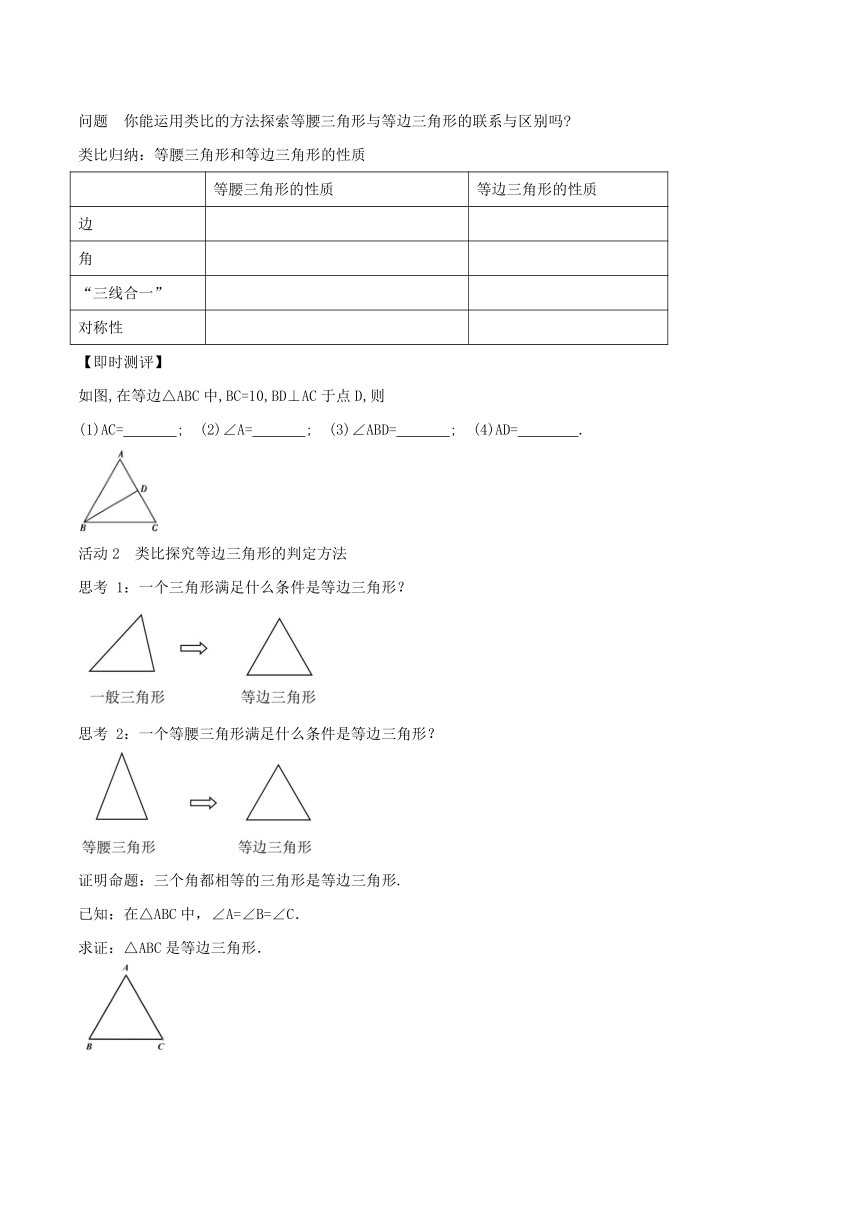
如图,在等边△ABC中,BC=10,BD⊥AC于点D,则
(1)AC= ; (2)∠A= ; (3)∠ABD= ; (4)AD= .
活动2 类比探究等边三角形的判定方法
思考 1:一个三角形满足什么条件是等边三角形?
思考 2:一个等腰三角形满足什么条件是等边三角形?
证明命题:三个角都相等的三角形是等边三角形.
已知:在△ABC中,∠A=∠B=∠C.
求证:△ABC是等边三角形.
归纳总结:等边三角形的判定:三个角都 的三角形是等边三角形.
符号语言:
问题 有一个角等于60°的等腰三角形是等边三角形吗 你能证明你的结论吗
归纳总结:等边三角形的判定:
有一个角为 的等腰三角形是等边三角形.
【即时测评】
根据条件判断下列三角形是否为等边三角形.
【例1】如图,△ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.
求证:△ADE是等边三角形.
变式训练
(1)如图1,若将条件DE∥BC改为AD=AE,△ADE还是等边三角形吗 试说明理由.
(2)如图2,若点D,E在边AB,AC的反向延长线上,且DE∥BC,结论依然成立吗
当堂达标
1. 下列关于“等边三角形”的说法不正确的是( )
A.等边三角形的三条边都相等
B.等边三角形的三个内角都相等且都等于60°
C.等边三角形是轴对称图形,有三条对称轴
D.等边三角形与等腰三角形具有相同的性质
2.给出下列几种三角形:①三个角都相等的三角形;②有两个角等于60°的三角形;③有一个角是60°的等腰三角形;④有两个角相等的等腰三角形.其中一定是等边三角形的有( )
A.0种 B.1种 C.2种 D.3种
3.在等边三角形ABC中,AD⊥BC于点D,则∠BAD=________°.
4.在等腰三角形ABC中,AB=AC,∠B=60°,则∠A=________°.
5.如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.
求证:BD=DE.
6.等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试证明你的结论.
课堂小结
(1)本节课学习了哪些主要内容
(2)我们是怎么探究等边三角形的性质和判定的
(3)本节课你学到了哪些方法
参考答案
当堂达标
1.D 2.D 3.30 4.60
5.证明:∵△ABC是等边三角形,BD平分∠ABC,
∴∠ABC=∠ACB=60°.∠DBC=30°.
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=30°.
∴∠DBC=∠DEC.
∴DB=DE.
6.解:△APQ为等边三角形.证明如下:
∵△ABC为等边三角形,
∴AB=AC.
∵BP=CQ,∠ABP=∠ACQ,
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
第1课时 等边三角形的性质与判定
学习目标
1.会阐述、推证等边三角形的性质和判定,掌握等边三角形的性质定理和判定定理.
2.在观察、猜想、证明等边三角形性质和判定的过程中,发展合情推理能力和演绎推理能力.
3.能运用等边三角形的性质和判定进行计算和证明,培养推理和运算能力及应用意识.
自主探索
1.等腰三角形有哪些性质和判定方法?
2.三角形怎样按边进行分类?
任务一 探究等边三角形的性质
问题 你能说出等边三角形的定义并结合图形写出符号语言吗
活动1 类比探究等边三角形的性质
问题 等腰三角形有哪些性质?
根据等边三角形与等腰三角形的关系,说出等边三角形有哪些性质?
如图所示,已知△ABC是等边三角形,求证:∠A=∠B=∠C.
归纳总结:等边三角形的三个内角都 ,并且每个角都等于 .
符号语言:
问题 你能运用类比的方法探索等腰三角形与等边三角形的联系与区别吗
类比归纳:等腰三角形和等边三角形的性质
等腰三角形的性质 等边三角形的性质
边
角
“三线合一”
对称性
【即时测评】
如图,在等边△ABC中,BC=10,BD⊥AC于点D,则
(1)AC= ; (2)∠A= ; (3)∠ABD= ; (4)AD= .
活动2 类比探究等边三角形的判定方法
思考 1:一个三角形满足什么条件是等边三角形?
思考 2:一个等腰三角形满足什么条件是等边三角形?
证明命题:三个角都相等的三角形是等边三角形.
已知:在△ABC中,∠A=∠B=∠C.
求证:△ABC是等边三角形.
归纳总结:等边三角形的判定:三个角都 的三角形是等边三角形.
符号语言:
问题 有一个角等于60°的等腰三角形是等边三角形吗 你能证明你的结论吗
归纳总结:等边三角形的判定:
有一个角为 的等腰三角形是等边三角形.
【即时测评】
根据条件判断下列三角形是否为等边三角形.
【例1】如图,△ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.
求证:△ADE是等边三角形.
变式训练
(1)如图1,若将条件DE∥BC改为AD=AE,△ADE还是等边三角形吗 试说明理由.
(2)如图2,若点D,E在边AB,AC的反向延长线上,且DE∥BC,结论依然成立吗
当堂达标
1. 下列关于“等边三角形”的说法不正确的是( )
A.等边三角形的三条边都相等
B.等边三角形的三个内角都相等且都等于60°
C.等边三角形是轴对称图形,有三条对称轴
D.等边三角形与等腰三角形具有相同的性质
2.给出下列几种三角形:①三个角都相等的三角形;②有两个角等于60°的三角形;③有一个角是60°的等腰三角形;④有两个角相等的等腰三角形.其中一定是等边三角形的有( )
A.0种 B.1种 C.2种 D.3种
3.在等边三角形ABC中,AD⊥BC于点D,则∠BAD=________°.
4.在等腰三角形ABC中,AB=AC,∠B=60°,则∠A=________°.
5.如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.
求证:BD=DE.
6.等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试证明你的结论.
课堂小结
(1)本节课学习了哪些主要内容
(2)我们是怎么探究等边三角形的性质和判定的
(3)本节课你学到了哪些方法
参考答案
当堂达标
1.D 2.D 3.30 4.60
5.证明:∵△ABC是等边三角形,BD平分∠ABC,
∴∠ABC=∠ACB=60°.∠DBC=30°.
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED=30°.
∴∠DBC=∠DEC.
∴DB=DE.
6.解:△APQ为等边三角形.证明如下:
∵△ABC为等边三角形,
∴AB=AC.
∵BP=CQ,∠ABP=∠ACQ,
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
同课章节目录
