15.3.2 等边三角形 第2课时 含30°角的直角三角形的性质 学案(含答案) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 15.3.2 等边三角形 第2课时 含30°角的直角三角形的性质 学案(含答案) 2025-2026学年数学人教版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 61.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 00:00:00 | ||
图片预览

文档简介
15.3.2 等边三角形
第2课时 含30°角的直角三角形的性质
学习目标
1.探索并掌握含30°角的直角三角形的性质,培养抽象概括能力.
2.会运用含30°角的直角三角形的性质进行简单计算和证明,培养运算能力和应用意识.
自主探索
1.等边三角形有哪些性质?
2.等边三角形有什么判定方法?
3.将两个含有30°角的直角三角尺摆放在一起,借助这个图形,你能找出图中的线段存在哪些数量关系吗
任务一 探究含30°角的直角三角形的性质
活动1 (1)如图,在△ABC中,∠C=90°,∠A=30°,测量∠A所对的直角边BC与斜边AB,你能得到什么结论
(2)怎样证明这个结论?说一说你的看法.
已知,如图所示,在Rt△ABC中,∠C=90°,∠A=30°.求证:BC=AB.
归纳总结:含 30 °角的直角三角形的性质定理:
在直角三角形中,如果一个锐角等于 30°,那么它所对的直角边等于斜边的 。
符号语言:
【即时测评】
判断下列说法是否正确:
(1)直角三角形中30°角所对的直角边等于另一直角边的一半.
(2)三角形中30°角所对的边等于最长边的一半。
(3)直角三角形中较短的直角边是斜边的一半。
(4)直角三角形的斜边是30°角所对直角边的2倍.
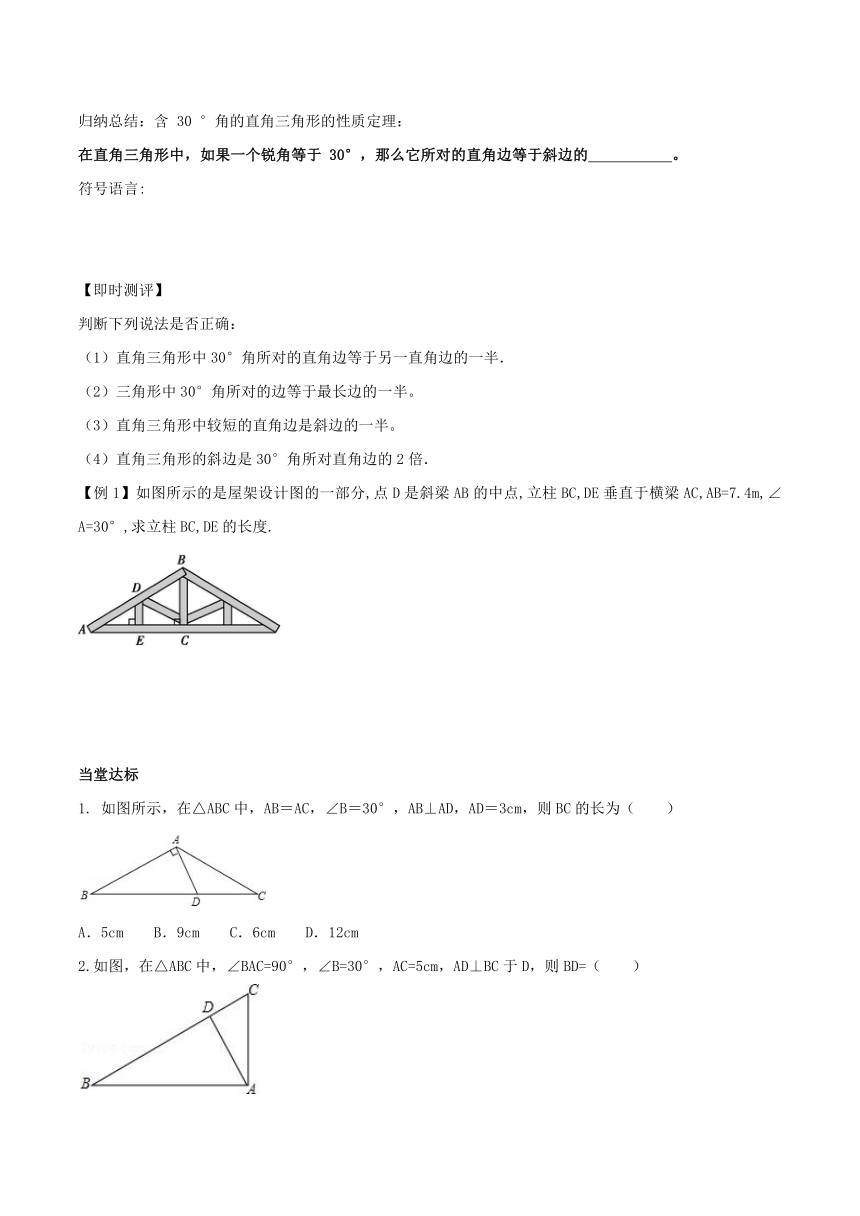
【例1】如图所示的是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,AB=7.4m,∠A=30°,求立柱BC,DE的长度.
当堂达标
1. 如图所示,在△ABC中,AB=AC,∠B=30°,AB⊥AD,AD=3cm,则BC的长为( )
A.5cm B.9cm C.6cm D.12cm
2.如图,在△ABC中,∠BAC=90°,∠B=30°,AC=5cm,AD⊥BC于D,则BD=( )
A.10cm B.7.5cm C.8.5cm D.6.5cm
3.如图,在等腰三角形ABC中,AB=AC=12 cm,∠BAC=120°,那么中线AD= cm.
4.已知:如图,∠C=90°, ∠B=30°,AD是∠BAC的平分线.
求证:BD=2CD.
5.在△ABC中 ,AB=AC,∠BAC=120° ,D是BC的中点,DE⊥AB于E点,求证:BE=3EA.
课堂小结
(1)本节课学习了哪些主要内容
(2)我们是怎么探究含30°的直角三角形的性质的
(3)含30°的直角三角形性质有什么作用
(4)本节课你学到了哪些方法
参考答案
当堂达标
1.B 2.B 3.6
4.证明:∵∠C=90°, ∠B=30°,
∴∠BAC=60°,
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD=30°,
∴∠B=∠BAD,
∴BD=AD,
在Rt△ACD中,∠CAD=30°,
∴AD=2CD,
∴BD=2CD.
5.证明:∵AB=AC,∠BAC=120°, ∴∠B=∠C=30°.
∵ D是BC的中点,∴AD⊥BC
∴∠ADC=90°,∠BAD=∠DAC=60°.
∴AB=2AD.
∵DE⊥AB,∴∠AED=90°,
∴∠ADE=30°,∴AD=2AE.
∴AB=4AE,∴BE=3AE.
第2课时 含30°角的直角三角形的性质
学习目标
1.探索并掌握含30°角的直角三角形的性质,培养抽象概括能力.
2.会运用含30°角的直角三角形的性质进行简单计算和证明,培养运算能力和应用意识.
自主探索
1.等边三角形有哪些性质?
2.等边三角形有什么判定方法?
3.将两个含有30°角的直角三角尺摆放在一起,借助这个图形,你能找出图中的线段存在哪些数量关系吗
任务一 探究含30°角的直角三角形的性质
活动1 (1)如图,在△ABC中,∠C=90°,∠A=30°,测量∠A所对的直角边BC与斜边AB,你能得到什么结论
(2)怎样证明这个结论?说一说你的看法.
已知,如图所示,在Rt△ABC中,∠C=90°,∠A=30°.求证:BC=AB.
归纳总结:含 30 °角的直角三角形的性质定理:
在直角三角形中,如果一个锐角等于 30°,那么它所对的直角边等于斜边的 。
符号语言:
【即时测评】
判断下列说法是否正确:
(1)直角三角形中30°角所对的直角边等于另一直角边的一半.
(2)三角形中30°角所对的边等于最长边的一半。
(3)直角三角形中较短的直角边是斜边的一半。
(4)直角三角形的斜边是30°角所对直角边的2倍.
【例1】如图所示的是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,AB=7.4m,∠A=30°,求立柱BC,DE的长度.
当堂达标
1. 如图所示,在△ABC中,AB=AC,∠B=30°,AB⊥AD,AD=3cm,则BC的长为( )
A.5cm B.9cm C.6cm D.12cm
2.如图,在△ABC中,∠BAC=90°,∠B=30°,AC=5cm,AD⊥BC于D,则BD=( )
A.10cm B.7.5cm C.8.5cm D.6.5cm
3.如图,在等腰三角形ABC中,AB=AC=12 cm,∠BAC=120°,那么中线AD= cm.
4.已知:如图,∠C=90°, ∠B=30°,AD是∠BAC的平分线.
求证:BD=2CD.
5.在△ABC中 ,AB=AC,∠BAC=120° ,D是BC的中点,DE⊥AB于E点,求证:BE=3EA.
课堂小结
(1)本节课学习了哪些主要内容
(2)我们是怎么探究含30°的直角三角形的性质的
(3)含30°的直角三角形性质有什么作用
(4)本节课你学到了哪些方法
参考答案
当堂达标
1.B 2.B 3.6
4.证明:∵∠C=90°, ∠B=30°,
∴∠BAC=60°,
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD=30°,
∴∠B=∠BAD,
∴BD=AD,
在Rt△ACD中,∠CAD=30°,
∴AD=2CD,
∴BD=2CD.
5.证明:∵AB=AC,∠BAC=120°, ∴∠B=∠C=30°.
∵ D是BC的中点,∴AD⊥BC
∴∠ADC=90°,∠BAD=∠DAC=60°.
∴AB=2AD.
∵DE⊥AB,∴∠AED=90°,
∴∠ADE=30°,∴AD=2AE.
∴AB=4AE,∴BE=3AE.
同课章节目录
