2.2.1 函数的单调性 课件 (4)

课件26张PPT。2.2 函数的简单性质
2.2.1 函数的单调性
第1课时 函数的单调性引导学生通过观察、归纳、抽象概括，自主构建单调增函数、单调减函数等概念.（难点）
能运用函数单调性概念解决简单的问题. (重点）
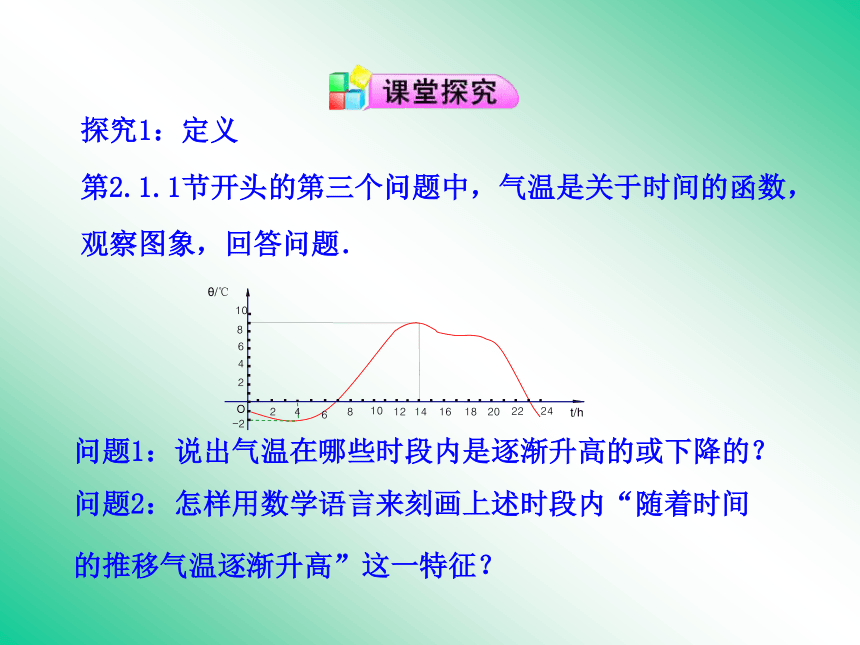
让学生领会数形结合的数学思想方法，培养学生发现问题、分析问题、解决问题的能力．抛物线的“上升”与“下降”反映了函数的什么性质？问题1：说出气温在哪些时段内是逐渐升高的或下降的？问题2：怎样用数学语言来刻画上述时段内“随着时间的推移气温逐渐升高”这一特征？探究1：定义
第2.1.1节开头的第三个问题中，气温是关于时间的函数，观察图象，回答问题．1.单调增函数
一般地，设函数y=f(x)的定义域为A，区间 I A.如果对于区间I内的任意两个值x1，x2，当x1函数值的变化一
致时函数单调递
增！2.单调减函数
如果对于区间I内的任意两个值x1，x2，当x1f(x2)，那么就说y=f(x)在区间I上是单调减函数，I称为y=f(x)的单调减区间.思考：类比单调增函数的定义说出单调减函数的定义 3.函数的单调性定义如果函数y=f(x)在区间I上是单调增函数或单调减函数，那么就说函数y=f(x)在区间I上具有单调性，单调增区间和单调减区间统称为单调区间.提升总结：2.单调性是对定义域内某个区间而言的，离开了定义域和相应区间就谈不上单调性，因此我们在求函数的单调区间时，要树立“定义域优先”的原则.在给定区间I上任取x1，x2
且x1则有函数f(x)在区间I上为单调增函数.
探究2:单调函数的图象表示图象上升为增函数！在给定区间I上任取x1，x2且x1f(x2）,
则有函数f(x)在区间I上为单调减函数.图象下降为减函数！单调增区间：[4，14]
单调减区间：[0，4]，[14，24]问题：请根据图象指出此函数的单调区间单调区间
之间用“，”
或“和”来连接！探究3： 想一想怎样证明函数f(x)=3x+2在R上是单调增函数？【解答】设x1，x2为R内的任意两个值，且x1所以f(x1)-f(x2）<0
即f(x1)故f(x)=3x+2在R上是单调增函数.提升总结：1.判断函数单调性的方法步骤： ① 任取x1，x2∈I，且x1单调减区间为[0，＋∞）．判断二次函数
的单调性
一看“开口方向”,
二看“对称轴”.图(2)（2）函数图象如图（2），（-∞ ，0）和（0，＋∞）是两个单调减区间.1证明：设x1，x2为区间（-∞ ，0 ）内的任意两个值，且x10.因为 所以 f(x1)-f(x2）<0 即 f(x1)故 在区间（-∞ ，0 ）上是单调增函数.本节课我们主要学习了：
1、函数单调性的定义．
2、判断、证明函数单调性的方法：图象法、定义法．忘掉失败，不过要牢记失败中的教训。