2.2.1 函数的单调性 课件

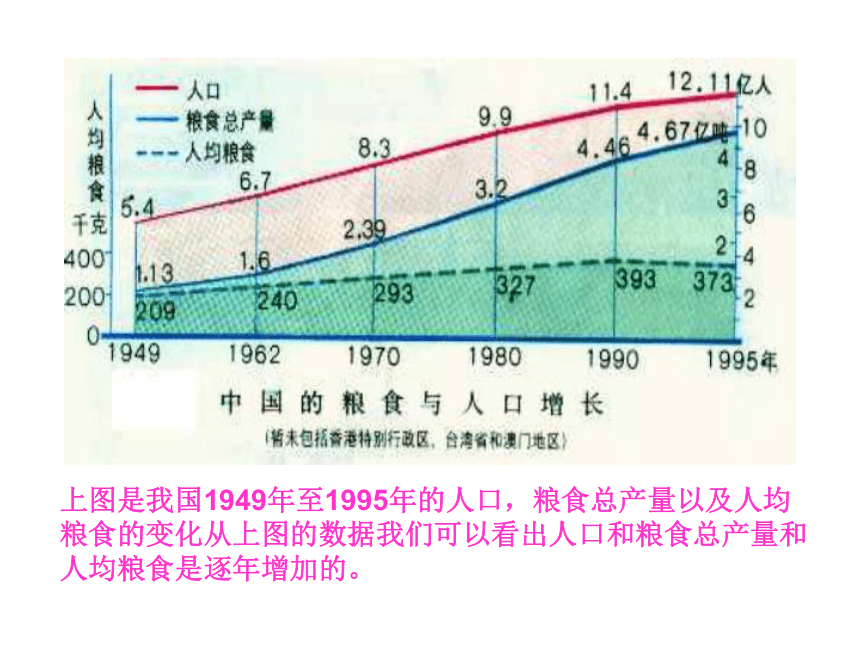
课件19张PPT。第2章 函数2.2.1 函数的单调性上图是我国1949年至1995年的人口，粮食总产量以及人均粮食的变化从上图的数据我们可以看出人口和粮食总产量和人均粮食是逐年增加的。能用图象上动点P（x，y）的横、纵坐标关系来说明上升或下降趋势吗？先下降后上升下降上升1.函数 在区间 上随着x的增大函数值也增大,那么在区间 上任意两个不同的 ,试问 与 有什么关系?2.能推广到一般的函数 在区间D上随着 的增大,相应的 值也增大(或减小),能用数学语言与符号表示吗?当 时, ;当 时, .思考:设函数y=f(x)的定义域为I,区间
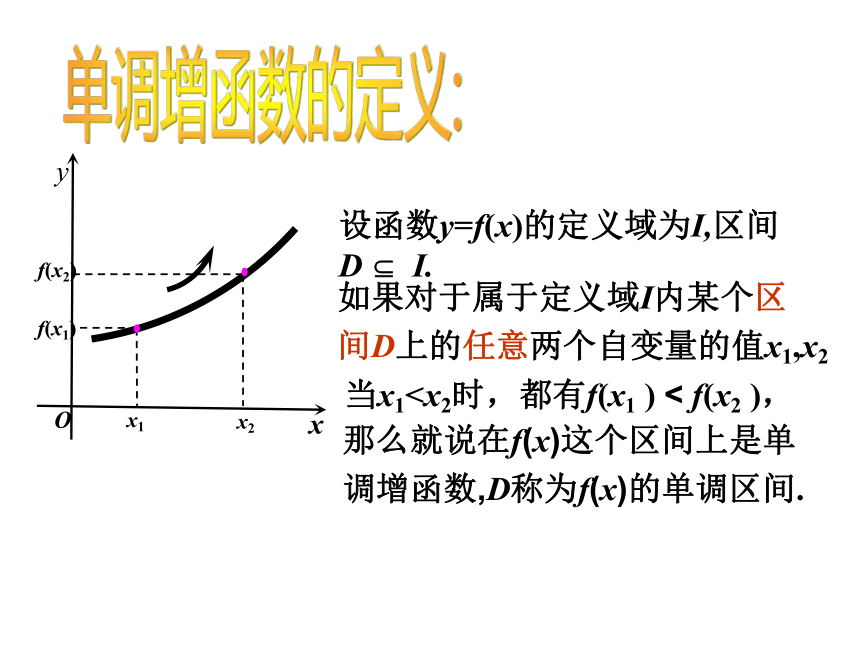
D I.如果对于属于定义域I内某个区
间D上的任意两个自变量的值x1,x2 那么就说在f(x)这个区间上是单
调增函数,D称为f(x)的单调区间.单调增函数的定义: 那么就说在f(x)这个区间上是单调增 函数，D称为f(x)的单调增区间. 那么就说在f(x)这个区间上是单调减
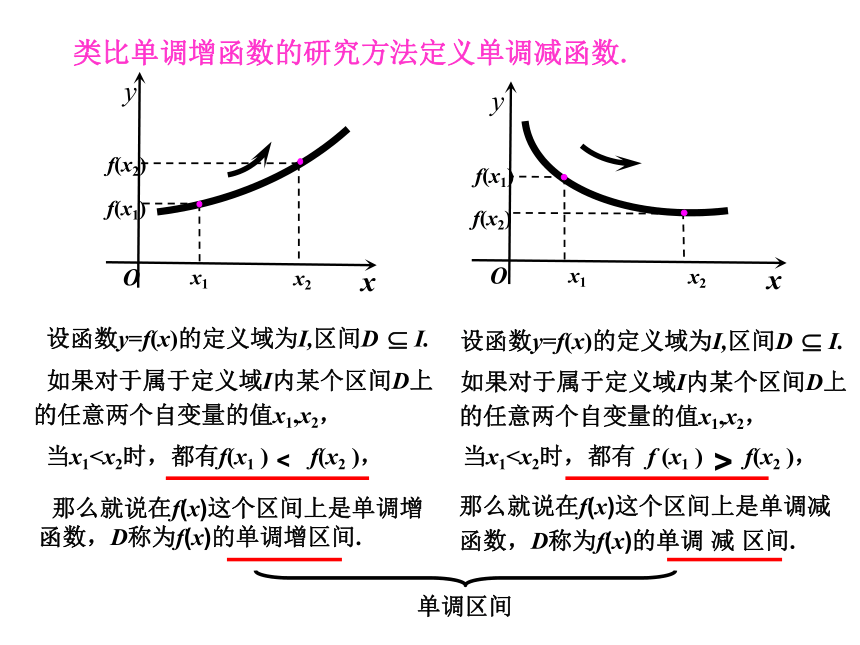
函数，D称为f(x)的单调 减 区间.类比单调增函数的研究方法定义单调减函数.设函数y=f(x)的定义域为I,区间D I. 如果对于属于定义域I内某个区间D上
的任意两个自变量的值x1,x2，设函数y=f(x)的定义域为I,区间D I. 如果对于属于定义域I内某个区间D上
的任意两个自变量的值x1,x2， 当x1单调区间判断1：函数f (x)= x2 在 是单调增函数；（1）如果函数 y =f(x)在区间D是单调增函数或单调减函数，那么就说函数 y =f(x)在区间D上具有单调性。在单调区间上，增函数的图象是上升的，减函数的图象是下降的。（2）函数单调性是针对某个区间而言的，是一个局部性质;答案：(不是)注意判断2：定义在R上的函数 f (x)满足 f (2)> f(1)，则函数 f (x)在R上是增函数；（3）x 1, x 2 取值的任意性例1 下图是定义在[－5，5]上的函数y＝f（x）的图象，根据图象说出y＝f（x）的单调区间，以及在每一单调区间上， y＝f（x）是增函数还是减函数.单调递增区间：[-2,1],[3,5]单调递减区间：[-5,-2),(-3,3)看下列函数图象,下列各函数有没有单调区间,若有写出其单调区间.图1图3图2没有单调区间减区间
增区间没有单调区间 画出函数 图象(1)这个函数的定义域是什么?(2)它在定义域I上的单调性是怎么样的?函数的定义域为_____________ 若将 改为 ,则函数的单调性又
如何?探究在 函数是单调递减的，在 函数也是单调递减的。例2.物理学中的玻意耳定律 (k为正常数)告诉我们,对于
一定量的气体,当其体积减小时,压强 p将增大,试用函数的单调
性证明之.取值定号结论证明函数单调性的一般步骤:取值作差变形定号结论练习2.证明函数在 上 是减函数.1.证明函数在 上 是减函数.证明证明思考:1.若 在R上是减函数,且 ,求实数m的取值范围.2.观察下列函数图象,除了单调性,你还能发现函数的哪些性质? 小结
1.函数单调性的定义中有哪些关键点？
2.判断函数单调性有哪些常用方法？
3.你学会了哪些数学思想方法？证明：在区间 上任取两个值 且 则，且所以函数 在区间上 是减函数. 证明：在区间 上任取两个值 且 则 ，且所以函数 在区间上 是减函数.