1.2 子集、全集、补集 学案(含答案解析)
文档属性
| 名称 | 1.2 子集、全集、补集 学案(含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 221.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-14 08:55:04 | ||
图片预览


文档简介
1.2
子集、全集、补集
学案
课时目标 1.理解子集、真子集的意义,会判断两集合的关系.2.理解全集与补集的意义,能正确运用补集的符号.3.会求集合的补集,并能运用Venn图及补集知识解决有关问题.
1.子集
如果集合A的__________元素都是集合B的元素(若a∈A则a∈B),那么集合A称为集合B的________,记作______或______.任何一个集合是它本身的______,即A A.
2.如果A B,并且A≠B,那么集合A称为集合B的________,记为______或(______).
3.______是任何集合的子集,______是任何非空集合的真子集.
4.补集
设A S,由S中不属于A的所有元素组成的集合称为S的子集A的______,记为______(读作“A在S中的补集”),即 SA={x|x∈S,且x A}.
5.全集
如果集合S包含我们所要研究的各个集合,这时S可以看做一个______,全集通常记作U.
集合A相对于全集U的补集用Venn图可表示为
一、填空题
1.集合P={x|y=},集合Q={y|y=},则P与Q的关系是________.
2.满足条件{1,2}M {1,2,3,4,5}的集合M的个数是________.
3.已知集合U={1,3,5,7,9},A={1,5,7},则 UA=________.
4.已知全集U=R,集合M={x|x2-4≤0},则 UM=________.
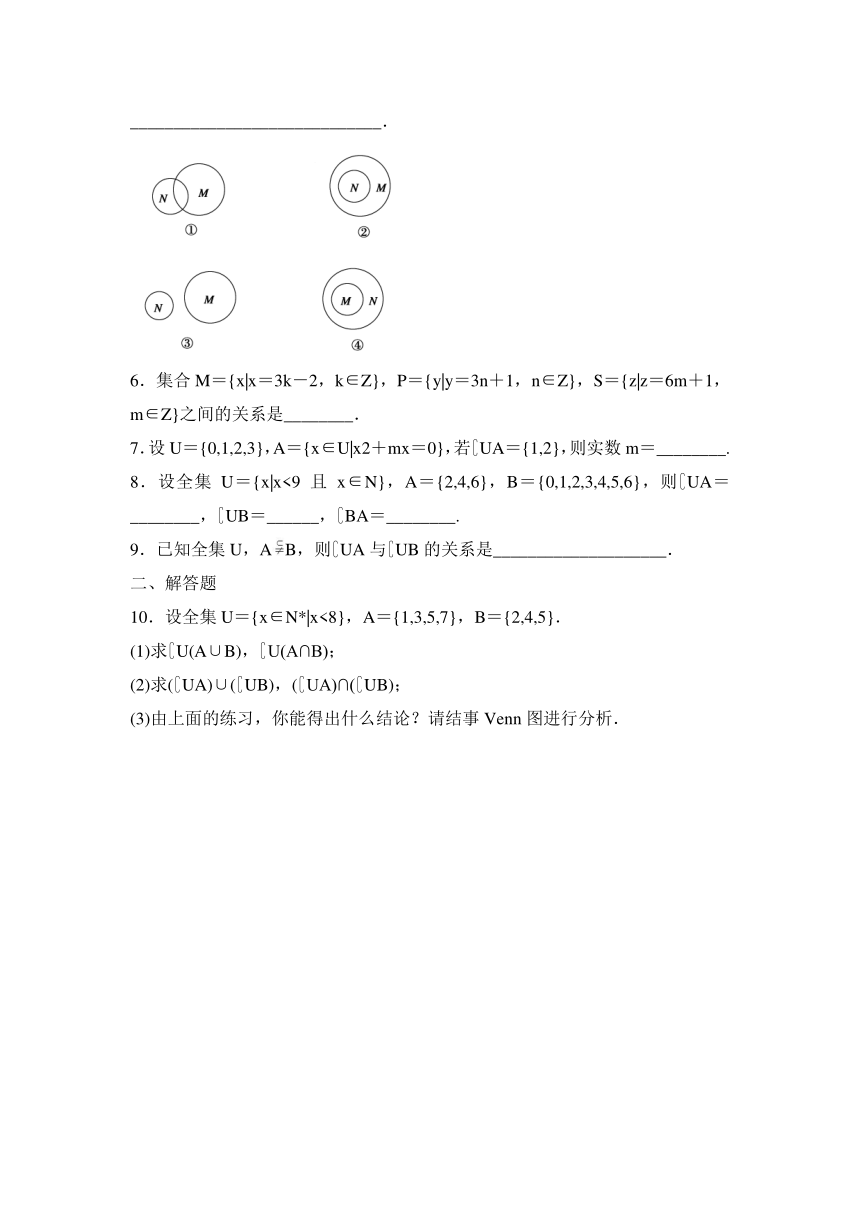
5.下列正确表示集合M={-1,0,1}和N={x|x2+x=0}关系的Venn图是_____________________________.
6.集合M={x|x=3k-2,k∈Z},P={y|y=3n+1,n∈Z},S={z|z=6m+1,m∈Z}之间的关系是________.
7.设U={0,1,2,3},A={x∈U|x2+mx=0},若 UA={1,2},则实数m=________.
8.设全集U={x|x<9且x∈N},A={2,4,6},B={0,1,2,3,4,5,6},则 UA=________, UB=______, BA=________.
9.已知全集U,AB,则 UA与 UB的关系是____________________.
二、解答题
10.设全集U={x∈N
|x<8},A={1,3,5,7},B={2,4,5}.
(1)求 U(A∪B), U(A∩B);
(2)求( UA)∪( UB),( UA)∩( UB);
(3)由上面的练习,你能得出什么结论?请结事Venn图进行分析.
11.已知集合A={1,3,x},B={1,x2},设集合U=A,求 UB.
能力提升
12.设全集是数集U={2,3,a2+2a-3},已知A={b,2}, UA={5},求实数a,b的值.
13.已知集合A={x|11.子集概念的多角度理解
(1)“A是B的子集”的含义是:集合A中的任何一个元素都是集合B的元素,即由任意x∈A能推出x∈B.
(2)不能把“A B”理解成“A是B中部分元素组成的集合”,因为当A= 时,A B,但A中不含任何元素;又当A=B时,也有A B,但A中含有B中的所有元素,这两种情况都有A B.
2. UA的数学意义包括两个方面:首先必须具备A U;其次是定义 UA={x|x∈U,且x A},补集是集合间的运算关系.
3.补集思想
做题时“正难则反”策略运用的是补集思想,即已知全集U,求子集A,若直接求A困难,可先求 UA,再由 U( UA)=A求A.
答案
知识梳理
1.任意一个 子集 A B B A 子集 2.真子集 AB BA
3.空集 空集 4.补集 SA 5.全集
作业设计
1.PQ
解析 ∵P={x|y=}={x|x≥-1},Q={y|y≥0},
∴PQ.
2.7
解析 M中含三个元素的个数为3,M中含四个元素的个数也是3,M中含5个元素的个数只有1个,因此符合题意的共7个.
3.{3,9}
解析 在集合U中,去掉1,5,7,剩下的元素构成 UA.
4.{x|x<-2或x>2}
解析 ∵M={x|-2≤x≤2},∴ UM={x|x<-2或x>2}.
5.②
解析 由N={-1,0},知N?M.
6.SP=M
解析 运用整数的性质方便求解.集合M、P表示成被3整除余1的整数集,集合S表示成被6整除余1的整数集.
7.-3
解析 ∵ UA={1,2},∴A={0,3},故m=-3.
8.{0,1,3,5,7,8} {7,8} {0,1,3,5}
解析 由题意得U={0,1,2,3,4,5,6,7,8},用Venn图表示出U,A,B,易得 UA={0,1,3,5,7,8}, UB={7,8}, BA={0,1,3,5}.
9. UB UA
解析 画Venn图,观察可知 UB UA.
10.解 (1)∵U={x∈N
|x<8}={1,2,3,4,5,6,7},A∪B={1,2,3,4,5,7},A∩B={5},∴ U(A∪B)={6}, U(A∩B)={1,2,3,4,67}.
(2)∵ UA={2,4,6}, UB={1,3,6,7},∴( UA)∪( UB)={1,2,3,4,6,7},( UA)∩( UB)={6}.
(3) U(A∪B)=( UA)∩( UB)(如左下图); U(A∩B)=( UA)∪( UB)(如右下图).
11.解 因为B A,因而x2=3或x2=x.
①若x2=3,则x=±.
当x=时,A={1,3,},B={1,3},此时 UB={};
当x=-时,A={1,3,-},B={1,3},U=A={1,3,-},此时 UB={-}.
②若x2=x,则x=0或x=1.
当x=1时,A中元素x与1相同,B中元素x2与1也相同,不符合元素的互异性,故x≠1;
当x=0时,A={1,3,0},B={1,0},U=A={1,3,0},从而 UB={3}.
综上所述, UB={}或{-}或{3}.
12.解 ∵ UA={5},∴5∈U且5 A.
又b∈A,∴b∈U,由此得
解得或经检验都符合题意.
13.解 (1)当a=0时,A= ,满足A B.
(2)当a>0时,A={x|又∵B={x|-1(3)当a<0时,A={x|∵A B,∴∴a≤-2.
综上所述,a=0或a≥2或a≤-2.
子集、全集、补集
学案
课时目标 1.理解子集、真子集的意义,会判断两集合的关系.2.理解全集与补集的意义,能正确运用补集的符号.3.会求集合的补集,并能运用Venn图及补集知识解决有关问题.
1.子集
如果集合A的__________元素都是集合B的元素(若a∈A则a∈B),那么集合A称为集合B的________,记作______或______.任何一个集合是它本身的______,即A A.
2.如果A B,并且A≠B,那么集合A称为集合B的________,记为______或(______).
3.______是任何集合的子集,______是任何非空集合的真子集.
4.补集
设A S,由S中不属于A的所有元素组成的集合称为S的子集A的______,记为______(读作“A在S中的补集”),即 SA={x|x∈S,且x A}.
5.全集
如果集合S包含我们所要研究的各个集合,这时S可以看做一个______,全集通常记作U.
集合A相对于全集U的补集用Venn图可表示为
一、填空题
1.集合P={x|y=},集合Q={y|y=},则P与Q的关系是________.
2.满足条件{1,2}M {1,2,3,4,5}的集合M的个数是________.
3.已知集合U={1,3,5,7,9},A={1,5,7},则 UA=________.
4.已知全集U=R,集合M={x|x2-4≤0},则 UM=________.
5.下列正确表示集合M={-1,0,1}和N={x|x2+x=0}关系的Venn图是_____________________________.
6.集合M={x|x=3k-2,k∈Z},P={y|y=3n+1,n∈Z},S={z|z=6m+1,m∈Z}之间的关系是________.
7.设U={0,1,2,3},A={x∈U|x2+mx=0},若 UA={1,2},则实数m=________.
8.设全集U={x|x<9且x∈N},A={2,4,6},B={0,1,2,3,4,5,6},则 UA=________, UB=______, BA=________.
9.已知全集U,AB,则 UA与 UB的关系是____________________.
二、解答题
10.设全集U={x∈N
|x<8},A={1,3,5,7},B={2,4,5}.
(1)求 U(A∪B), U(A∩B);
(2)求( UA)∪( UB),( UA)∩( UB);
(3)由上面的练习,你能得出什么结论?请结事Venn图进行分析.
11.已知集合A={1,3,x},B={1,x2},设集合U=A,求 UB.
能力提升
12.设全集是数集U={2,3,a2+2a-3},已知A={b,2}, UA={5},求实数a,b的值.
13.已知集合A={x|1
(1)“A是B的子集”的含义是:集合A中的任何一个元素都是集合B的元素,即由任意x∈A能推出x∈B.
(2)不能把“A B”理解成“A是B中部分元素组成的集合”,因为当A= 时,A B,但A中不含任何元素;又当A=B时,也有A B,但A中含有B中的所有元素,这两种情况都有A B.
2. UA的数学意义包括两个方面:首先必须具备A U;其次是定义 UA={x|x∈U,且x A},补集是集合间的运算关系.
3.补集思想
做题时“正难则反”策略运用的是补集思想,即已知全集U,求子集A,若直接求A困难,可先求 UA,再由 U( UA)=A求A.
答案
知识梳理
1.任意一个 子集 A B B A 子集 2.真子集 AB BA
3.空集 空集 4.补集 SA 5.全集
作业设计
1.PQ
解析 ∵P={x|y=}={x|x≥-1},Q={y|y≥0},
∴PQ.
2.7
解析 M中含三个元素的个数为3,M中含四个元素的个数也是3,M中含5个元素的个数只有1个,因此符合题意的共7个.
3.{3,9}
解析 在集合U中,去掉1,5,7,剩下的元素构成 UA.
4.{x|x<-2或x>2}
解析 ∵M={x|-2≤x≤2},∴ UM={x|x<-2或x>2}.
5.②
解析 由N={-1,0},知N?M.
6.SP=M
解析 运用整数的性质方便求解.集合M、P表示成被3整除余1的整数集,集合S表示成被6整除余1的整数集.
7.-3
解析 ∵ UA={1,2},∴A={0,3},故m=-3.
8.{0,1,3,5,7,8} {7,8} {0,1,3,5}
解析 由题意得U={0,1,2,3,4,5,6,7,8},用Venn图表示出U,A,B,易得 UA={0,1,3,5,7,8}, UB={7,8}, BA={0,1,3,5}.
9. UB UA
解析 画Venn图,观察可知 UB UA.
10.解 (1)∵U={x∈N
|x<8}={1,2,3,4,5,6,7},A∪B={1,2,3,4,5,7},A∩B={5},∴ U(A∪B)={6}, U(A∩B)={1,2,3,4,67}.
(2)∵ UA={2,4,6}, UB={1,3,6,7},∴( UA)∪( UB)={1,2,3,4,6,7},( UA)∩( UB)={6}.
(3) U(A∪B)=( UA)∩( UB)(如左下图); U(A∩B)=( UA)∪( UB)(如右下图).
11.解 因为B A,因而x2=3或x2=x.
①若x2=3,则x=±.
当x=时,A={1,3,},B={1,3},此时 UB={};
当x=-时,A={1,3,-},B={1,3},U=A={1,3,-},此时 UB={-}.
②若x2=x,则x=0或x=1.
当x=1时,A中元素x与1相同,B中元素x2与1也相同,不符合元素的互异性,故x≠1;
当x=0时,A={1,3,0},B={1,0},U=A={1,3,0},从而 UB={3}.
综上所述, UB={}或{-}或{3}.
12.解 ∵ UA={5},∴5∈U且5 A.
又b∈A,∴b∈U,由此得
解得或经检验都符合题意.
13.解 (1)当a=0时,A= ,满足A B.
(2)当a>0时,A={x|
综上所述,a=0或a≥2或a≤-2.
