人教版八年级数学上册第15章轴对称15.2画轴对称的图形第1课时轴对称的图形的画法 课件(共20张PPT)
文档属性
| 名称 | 人教版八年级数学上册第15章轴对称15.2画轴对称的图形第1课时轴对称的图形的画法 课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 15.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 22:31:55 | ||
图片预览






文档简介
(共20张PPT)
1.能够按要求画简单平面图形经过一次对称后的图形.
2.掌握作轴对称图形的方法.
3.通过画轴对称图形,增强学生学习几何的趣味感.
会画已知图形关于某直线的轴对称图形.
理解轴对称性质在作图中的应用.
难点
重点
已知一个图形和一条直线,如何画出与这个图形关于这条直线对称的图形呢?
如图,在一张半透明纸的左边部分,画一只左脚印,把这张纸对折后描图,打开对折的纸,就能得到相应的右脚印.
(1)认真观察,左脚印和右脚印有什么关系?
成轴对称
(2)对称轴与折痕及图中的线段PP ′分别是什么关系?
对称轴是折痕所在的直线,即直线l,直线l垂直平分线段PP′.
类似地,请你再画一个图形做一做,看看能否得到同样的结论?
由一个平面图形可以得到与它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全相同;新图形上的每一点都是原图形上的某一点关于直线l的对称点;连接任意一对对称点的线段被对称轴垂直平分.
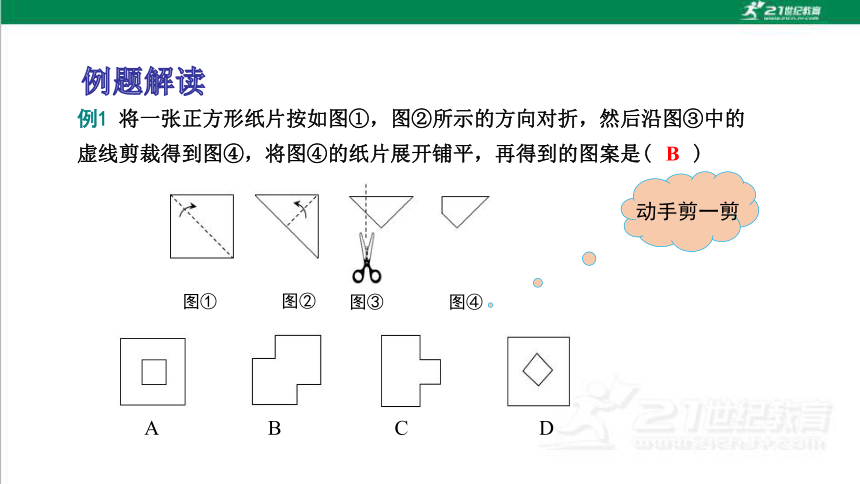
例1 将一张正方形纸片按如图①,图②所示的方向对折,然后沿图③中的虚线剪裁得到图④,将图④的纸片展开铺平,再得到的图案是( )
图①
图②
图③
图④
A
B
C
D
B
动手剪一剪
问题1 如何画一个点的轴对称图形?
画出点A关于直线l的对称点A′.
﹒
l
A
﹒
A′
O
作法:
(1)过点A作l的垂线,垂足为点O.
(2)在垂线上截取OA′=OA.
点A′就是点A关于直线l的对称点.
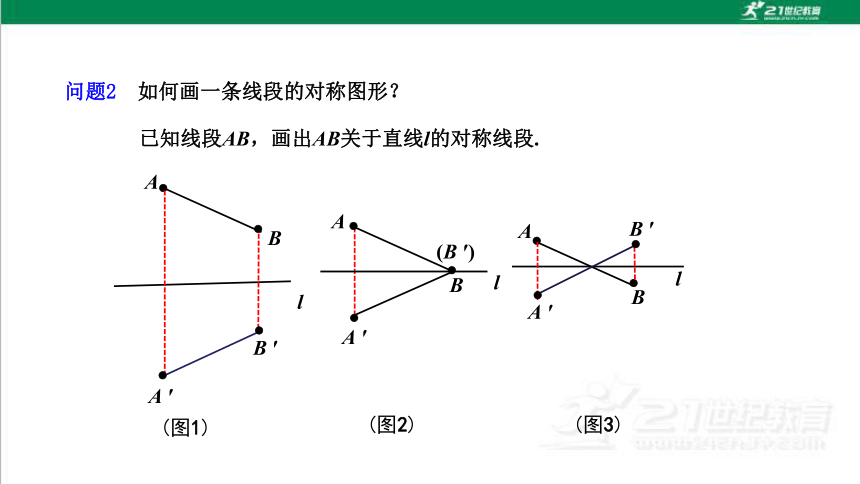
问题2 如何画一条线段的对称图形?
已知线段AB,画出AB关于直线l的对称线段.
A
B
(图1)
(图2)
(图3)
A
B
l
l
A
B
l
A ′
A ′
A ′
B ′
(B ′)
B ′
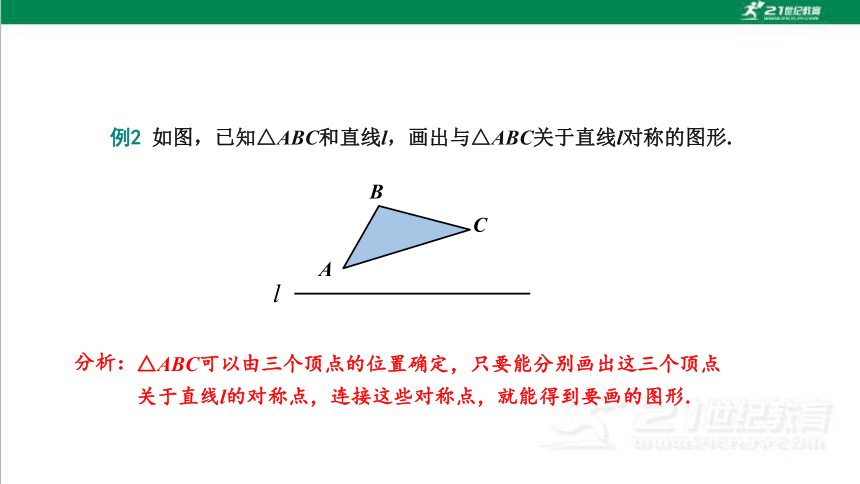
例2 如图,已知△ABC和直线l,画出与△ABC关于直线l对称的图形.
A
B
C
△ABC可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要画的图形.
分析:
画法:
(1)过点A画直线l的垂线,垂足为O,在垂线上截取OA′=OA,A′就是点A关于直线l的对称点.
(3)连接A′B′,B′C′,C′A′,则△ A′B′C′
即为所求.
(2)同理,分别画出点B,C关于直线l的对称点B′,C′ .
A
B
C
A′
B′
C′
O
画轴对称图形的方法
找:在原图形上找特殊点;
画:画出各个特殊点关于对称轴的对称点;
连:连接这些对称点,就可以得到与原图形成轴对称的图形.
线段的端点,线与线的交点、中点等
如图给出了一个图案的一半,其中的虚线 l 是这个图案的对称轴. 整个图案是个什么形状?请准确地画出它的另一半.
B
A
C
D
E
F
G
H
l
作图原理
对称轴是对称点连线段的垂直平分线.
(1)找特殊点;
(2)作垂线;
(3)截取等长;
(4)依次连线.
作图方法
1.作已知点关于某直线的对称点的第一步是( )
A.过已知点作一条直线与已知直线相交
B.过已知点作一条直线与已知直线垂直
C.过已知点作一条直线与已知直线平行
D.不确定
B
2.如图所示是一只停泊在平静水面上的小船,它的“倒影”应是( )
B
3.下面是四名同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
B
4. 如图,把下列图形补成关于直线 l 对称的轴对称图形.
l
l
作轴对称图形的口诀:作垂线,截等线,顺次连.
5. 如图,画△ABC关于直线m的对称图形.
m
A
B
C
(A ′)
C ′
B ′
6.如图,正三角形网格中,已有两个小三角形被涂黑.
(1)再将图①中其余小三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形(画出两种不同的);
解:如图①所示.
(2)再将图②中其余小三角形涂黑两个,使整个被涂黑的图案构成一个轴对称图形(画出两种不同的).
解:如图②所示.
(答案不唯一)
1.能够按要求画简单平面图形经过一次对称后的图形.
2.掌握作轴对称图形的方法.
3.通过画轴对称图形,增强学生学习几何的趣味感.
会画已知图形关于某直线的轴对称图形.
理解轴对称性质在作图中的应用.
难点
重点
已知一个图形和一条直线,如何画出与这个图形关于这条直线对称的图形呢?
如图,在一张半透明纸的左边部分,画一只左脚印,把这张纸对折后描图,打开对折的纸,就能得到相应的右脚印.
(1)认真观察,左脚印和右脚印有什么关系?
成轴对称
(2)对称轴与折痕及图中的线段PP ′分别是什么关系?
对称轴是折痕所在的直线,即直线l,直线l垂直平分线段PP′.
类似地,请你再画一个图形做一做,看看能否得到同样的结论?
由一个平面图形可以得到与它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全相同;新图形上的每一点都是原图形上的某一点关于直线l的对称点;连接任意一对对称点的线段被对称轴垂直平分.
例1 将一张正方形纸片按如图①,图②所示的方向对折,然后沿图③中的虚线剪裁得到图④,将图④的纸片展开铺平,再得到的图案是( )
图①
图②
图③
图④
A
B
C
D
B
动手剪一剪
问题1 如何画一个点的轴对称图形?
画出点A关于直线l的对称点A′.
﹒
l
A
﹒
A′
O
作法:
(1)过点A作l的垂线,垂足为点O.
(2)在垂线上截取OA′=OA.
点A′就是点A关于直线l的对称点.
问题2 如何画一条线段的对称图形?
已知线段AB,画出AB关于直线l的对称线段.
A
B
(图1)
(图2)
(图3)
A
B
l
l
A
B
l
A ′
A ′
A ′
B ′
(B ′)
B ′
例2 如图,已知△ABC和直线l,画出与△ABC关于直线l对称的图形.
A
B
C
△ABC可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要画的图形.
分析:
画法:
(1)过点A画直线l的垂线,垂足为O,在垂线上截取OA′=OA,A′就是点A关于直线l的对称点.
(3)连接A′B′,B′C′,C′A′,则△ A′B′C′
即为所求.
(2)同理,分别画出点B,C关于直线l的对称点B′,C′ .
A
B
C
A′
B′
C′
O
画轴对称图形的方法
找:在原图形上找特殊点;
画:画出各个特殊点关于对称轴的对称点;
连:连接这些对称点,就可以得到与原图形成轴对称的图形.
线段的端点,线与线的交点、中点等
如图给出了一个图案的一半,其中的虚线 l 是这个图案的对称轴. 整个图案是个什么形状?请准确地画出它的另一半.
B
A
C
D
E
F
G
H
l
作图原理
对称轴是对称点连线段的垂直平分线.
(1)找特殊点;
(2)作垂线;
(3)截取等长;
(4)依次连线.
作图方法
1.作已知点关于某直线的对称点的第一步是( )
A.过已知点作一条直线与已知直线相交
B.过已知点作一条直线与已知直线垂直
C.过已知点作一条直线与已知直线平行
D.不确定
B
2.如图所示是一只停泊在平静水面上的小船,它的“倒影”应是( )
B
3.下面是四名同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
B
4. 如图,把下列图形补成关于直线 l 对称的轴对称图形.
l
l
作轴对称图形的口诀:作垂线,截等线,顺次连.
5. 如图,画△ABC关于直线m的对称图形.
m
A
B
C
(A ′)
C ′
B ′
6.如图,正三角形网格中,已有两个小三角形被涂黑.
(1)再将图①中其余小三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形(画出两种不同的);
解:如图①所示.
(2)再将图②中其余小三角形涂黑两个,使整个被涂黑的图案构成一个轴对称图形(画出两种不同的).
解:如图②所示.
(答案不唯一)
同课章节目录
