人教版八年级数学上册第15章轴对称15.2画轴对称的图形第2课时用坐标表示轴对称 课件(共19张PPT)
文档属性
| 名称 | 人教版八年级数学上册第15章轴对称15.2画轴对称的图形第2课时用坐标表示轴对称 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 19.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 05:15:31 | ||
图片预览




文档简介
(共19张PPT)
1.探究在平面直角坐标系中关于x轴和y轴对称点的坐标特点.
2.能在平面直角坐标系中画出一些简单的关于x轴和y轴的对称图形.
3.能根据坐标系中轴对称点的坐标特点解决简单的问题.
在直角坐标系中关于x轴和y轴对称点的坐标变化规律,利用坐标变化规律作出关于x轴和y轴的对称图形.
找对称点之间坐标关系、规律.
难点
重点
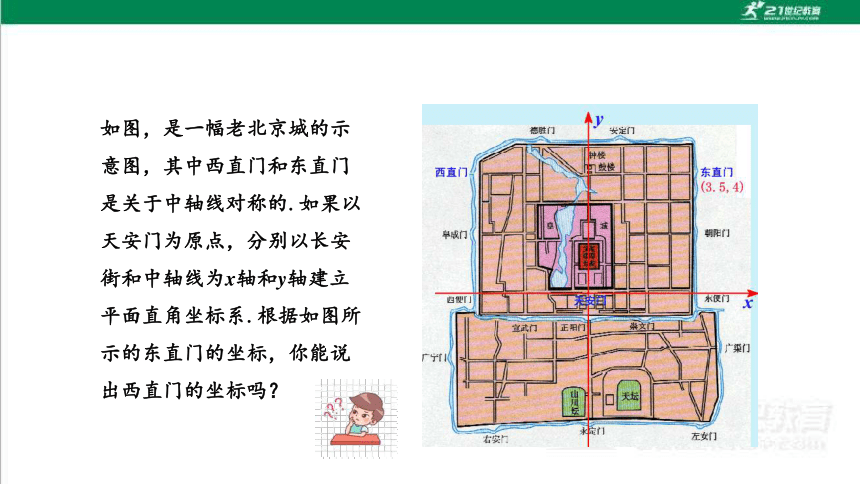
一位游客在天安门广场询问小明西直门的位置,但他只知道东直门的位置,聪明的小明想了想,就准确的告诉了他,你能猜到小明是怎么做的吗?
如图,是一幅老北京城的示意图,其中西直门和东直门是关于中轴线对称的.如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系.根据如图所示的东直门的坐标,你能说出西直门的坐标吗?
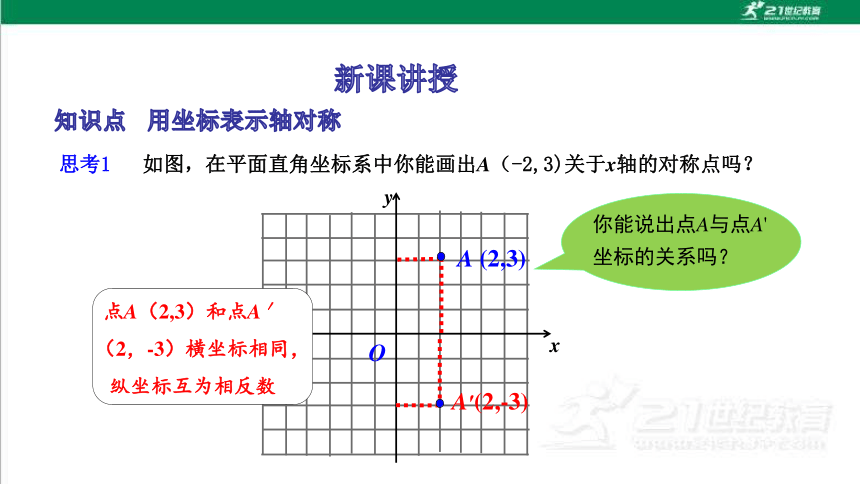
思考1 如图,在平面直角坐标系中你能画出A(-2,3)关于x轴的对称点吗?
x
y
O
A (2,3)
A′(2,-3)
你能说出点A与点A'坐标的关系吗?
点A(2,3)和点A′(2,-3)横坐标相同,纵坐标互为相反数
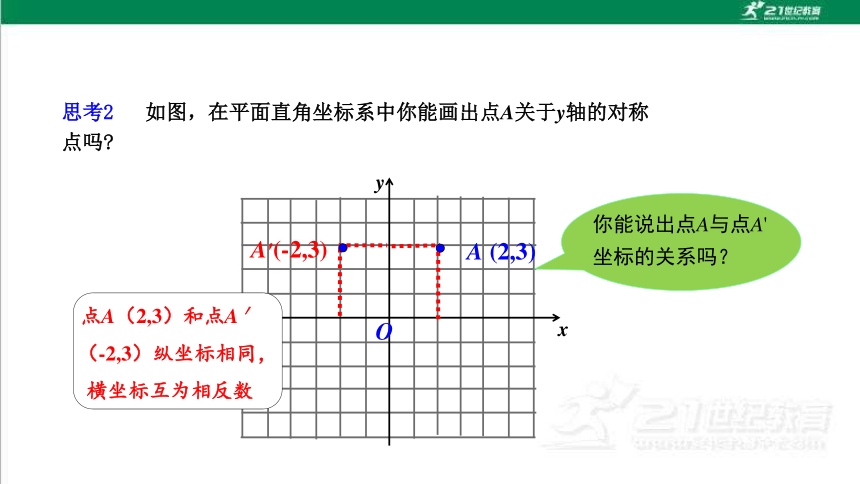
思考2 如图,在平面直角坐标系中你能画出点A关于y轴的对称点吗
x
y
O
A (2,3)
A′(-2,3)
你能说出点A与点A'坐标的关系吗?
点A(2,3)和点A′
(-2,3)纵坐标相同,横坐标互为相反数
在平面直角坐标系中,画出下列已知点及其关于坐标轴的对称点, 并把它们的坐标填入表格中,看一看每对对称点的坐标有怎样的规律,再和同学讨论一下.
已知点 A(2,-3) B(-1,2) C(-6,-5) E(4,0)
关于x轴的对称点
关于y轴的对称点
探究
已知点 A(2,-3) B(-1,2) C(-6,-5) E(4,0)
关于x轴的对称点 A′(2,3) B′(-1,-2) C′(-6,5) E′(4,0)
已知点 A(2,-3) B(-1,2) C(-6,-5) E(4,0)
关于y轴对称点 A′′(-2,-3) B′′(1,2) C′′(6,-5) E′′(-4,0)
已知点 A(2,-3) B(-1,2) C(-6,-5) E(4,0)
关于x轴的对称点 A′(2,3) B′(-1,-2) C′(-6,5) E′(4,0)
关于y轴对称点 A′′(-2,-3) B′′(1,2) C′′(6,-5) E′′(-4,0)
根据表格所填的坐标,你发现了什么规律?
关于坐标轴对称的点的坐标规律
1.点(x,y)关于x轴对称的点的坐标为(x,-y);
2.点(x,y)关于y轴对称的点的坐标为(-x,y).
横坐标相同,纵坐标互为相反数.
纵坐标相同,横坐标互为相反数.
例1 如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),C(-2,5),
D(-5,4),分别画出与四边形ABCD关于y轴和x轴对称的图形.
x
y
A
B
C
D
A ′
B ′
C ′
D ′
A ′
B ′
C ′
D ′
O
坐标系中画轴对称图形的方法
计算:计算出已知图形中的一些特殊点的对称点的坐标;
描点:根据对称点的坐标描点;
连接:按原图对应点连接所描各点得到对称图形.
所找的特殊点一定要能确定原图形, 否则画出的图形与原图形不一定成轴对称.
1. 平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,-1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)若△ABC与△A'B'C'关于x轴对称,画出△A'B'C',并写出A'、B'、C'的坐标.
x
y
O
A (0,4)
B (2,4)
C (3,-1)
A' (0,-4)
B' (2,-4)
C' (3,1)
解:如图所示:
关于坐标轴对称的点的坐标特征
关于x轴对称,横同纵反;关于y轴对称,横反纵同
计算
描点
连接
在坐标系中作已知图形的对称图形
1.完成下表.
已知点 (2,-3) (-1,2) (-6,-5) (0,-1.6) (4,0)
关于x轴的对称点
关于y轴的对称点
(-2, -3)
(2,3)
(-1,-2)
(1, 2)
(6, -5)
(-6, 5)
(0, -1.6)
(0,1.6)
(-4,0)
(4,0)
2.已知点P(2a+b,-3a)与点P′(8,b+2).
若点P与点P′关于x轴对称,则a=_____, b=_______.
若点P与点P′关于y轴对称,则a=_____ ,b=_______.
2
4
6
-20
3.已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),C(-1,3),
作出△ABC关于y轴对称的图形.
解:点A(-3,5),B(-4,1),C(-1,3),
关于y轴对称点的坐标分别为
A ′(3,5),B ′(4,1),C ′(1,3).依次连接
A ′ B ′,B ′ C ′,C ′ A ′,就得到△ABC关于y轴对称的△A ′ B ′ C ′.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A
C
B
B ′
A′
C ′
x
y
4. 已知点A(2a+b,-4),B(3,a-2b)关于x轴对称,求点C(a,b)在第几象限?
解:∵点A(2a+b,-4),B(3,a-2b)关于x轴对称,
∴2a+b=3,a-2b=4,
解得a=2,b=-1.
∴点C(2,-1)在第四象限.
1.探究在平面直角坐标系中关于x轴和y轴对称点的坐标特点.
2.能在平面直角坐标系中画出一些简单的关于x轴和y轴的对称图形.
3.能根据坐标系中轴对称点的坐标特点解决简单的问题.
在直角坐标系中关于x轴和y轴对称点的坐标变化规律,利用坐标变化规律作出关于x轴和y轴的对称图形.
找对称点之间坐标关系、规律.
难点
重点
一位游客在天安门广场询问小明西直门的位置,但他只知道东直门的位置,聪明的小明想了想,就准确的告诉了他,你能猜到小明是怎么做的吗?
如图,是一幅老北京城的示意图,其中西直门和东直门是关于中轴线对称的.如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系.根据如图所示的东直门的坐标,你能说出西直门的坐标吗?
思考1 如图,在平面直角坐标系中你能画出A(-2,3)关于x轴的对称点吗?
x
y
O
A (2,3)
A′(2,-3)
你能说出点A与点A'坐标的关系吗?
点A(2,3)和点A′(2,-3)横坐标相同,纵坐标互为相反数
思考2 如图,在平面直角坐标系中你能画出点A关于y轴的对称点吗
x
y
O
A (2,3)
A′(-2,3)
你能说出点A与点A'坐标的关系吗?
点A(2,3)和点A′
(-2,3)纵坐标相同,横坐标互为相反数
在平面直角坐标系中,画出下列已知点及其关于坐标轴的对称点, 并把它们的坐标填入表格中,看一看每对对称点的坐标有怎样的规律,再和同学讨论一下.
已知点 A(2,-3) B(-1,2) C(-6,-5) E(4,0)
关于x轴的对称点
关于y轴的对称点
探究
已知点 A(2,-3) B(-1,2) C(-6,-5) E(4,0)
关于x轴的对称点 A′(2,3) B′(-1,-2) C′(-6,5) E′(4,0)
已知点 A(2,-3) B(-1,2) C(-6,-5) E(4,0)
关于y轴对称点 A′′(-2,-3) B′′(1,2) C′′(6,-5) E′′(-4,0)
已知点 A(2,-3) B(-1,2) C(-6,-5) E(4,0)
关于x轴的对称点 A′(2,3) B′(-1,-2) C′(-6,5) E′(4,0)
关于y轴对称点 A′′(-2,-3) B′′(1,2) C′′(6,-5) E′′(-4,0)
根据表格所填的坐标,你发现了什么规律?
关于坐标轴对称的点的坐标规律
1.点(x,y)关于x轴对称的点的坐标为(x,-y);
2.点(x,y)关于y轴对称的点的坐标为(-x,y).
横坐标相同,纵坐标互为相反数.
纵坐标相同,横坐标互为相反数.
例1 如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),C(-2,5),
D(-5,4),分别画出与四边形ABCD关于y轴和x轴对称的图形.
x
y
A
B
C
D
A ′
B ′
C ′
D ′
A ′
B ′
C ′
D ′
O
坐标系中画轴对称图形的方法
计算:计算出已知图形中的一些特殊点的对称点的坐标;
描点:根据对称点的坐标描点;
连接:按原图对应点连接所描各点得到对称图形.
所找的特殊点一定要能确定原图形, 否则画出的图形与原图形不一定成轴对称.
1. 平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,-1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)若△ABC与△A'B'C'关于x轴对称,画出△A'B'C',并写出A'、B'、C'的坐标.
x
y
O
A (0,4)
B (2,4)
C (3,-1)
A' (0,-4)
B' (2,-4)
C' (3,1)
解:如图所示:
关于坐标轴对称的点的坐标特征
关于x轴对称,横同纵反;关于y轴对称,横反纵同
计算
描点
连接
在坐标系中作已知图形的对称图形
1.完成下表.
已知点 (2,-3) (-1,2) (-6,-5) (0,-1.6) (4,0)
关于x轴的对称点
关于y轴的对称点
(-2, -3)
(2,3)
(-1,-2)
(1, 2)
(6, -5)
(-6, 5)
(0, -1.6)
(0,1.6)
(-4,0)
(4,0)
2.已知点P(2a+b,-3a)与点P′(8,b+2).
若点P与点P′关于x轴对称,则a=_____, b=_______.
若点P与点P′关于y轴对称,则a=_____ ,b=_______.
2
4
6
-20
3.已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),C(-1,3),
作出△ABC关于y轴对称的图形.
解:点A(-3,5),B(-4,1),C(-1,3),
关于y轴对称点的坐标分别为
A ′(3,5),B ′(4,1),C ′(1,3).依次连接
A ′ B ′,B ′ C ′,C ′ A ′,就得到△ABC关于y轴对称的△A ′ B ′ C ′.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A
C
B
B ′
A′
C ′
x
y
4. 已知点A(2a+b,-4),B(3,a-2b)关于x轴对称,求点C(a,b)在第几象限?
解:∵点A(2a+b,-4),B(3,a-2b)关于x轴对称,
∴2a+b=3,a-2b=4,
解得a=2,b=-1.
∴点C(2,-1)在第四象限.
同课章节目录
