人教版八年级数学上册第15章轴对称15.3.1等腰三角形第2课时等腰三角形的判定 课件(共18张PPT)
文档属性
| 名称 | 人教版八年级数学上册第15章轴对称15.3.1等腰三角形第2课时等腰三角形的判定 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 14.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 05:14:12 | ||
图片预览




文档简介
(共18张PPT)
难点
重点
理解和运用等腰三角形的判定定理.
1.掌握等腰三角形的判定定理.
2.能运“等腰三角形的判定定理”进行证明和计算.
3.培养论证几何图形问题的能力,体会证明的必要性.
探索并掌握等腰三角形的判定的过程,并用以解决实际问题.
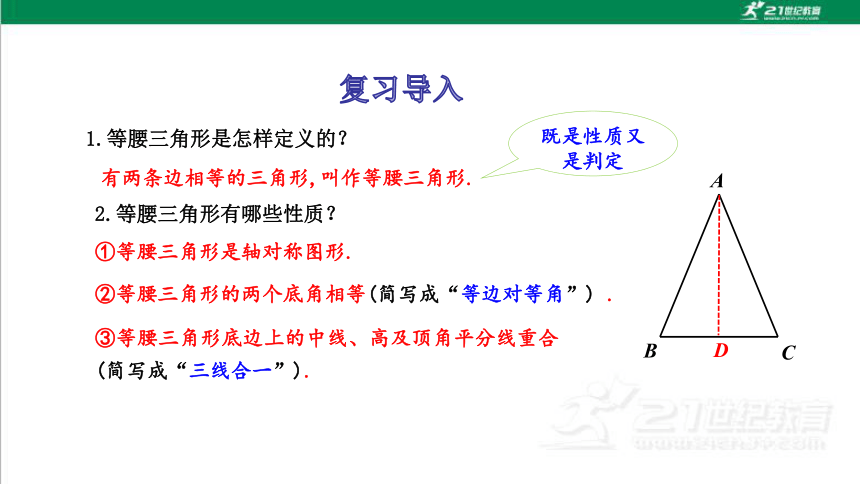
1.等腰三角形是怎样定义的?
有两条边相等的三角形,叫作等腰三角形.
①等腰三角形是轴对称图形.
③等腰三角形底边上的中线、高及顶角平分线重合(简写成“三线合一”).
②等腰三角形的两个底角相等(简写成“等边对等角”) .
2.等腰三角形有哪些性质?
既是性质又是判定
A
B
C
D
思考 我们知道,如果一个三角形有两条边相等,那么它们所对的角相等. 反过来,如果一个三角形有两个角相等,那么它们所对的边有什么关系?
猜想 如果一个三角形有两个角相等,那么它们所对的边相等.
你能证明这个结论吗?
已知:如图,在△ABC中,∠B=∠C.
求证:AB=AC.
如图,作△ABC的角平分线AD.
在△ABD和△ACD中,
∠B=∠C,
∠BAD=∠CAD,
AD=AD,
∴△ABD≌△ACD(AAS).
∴ AB=AC.
证明:
A
C
B
D
你能得到什么结论呢?
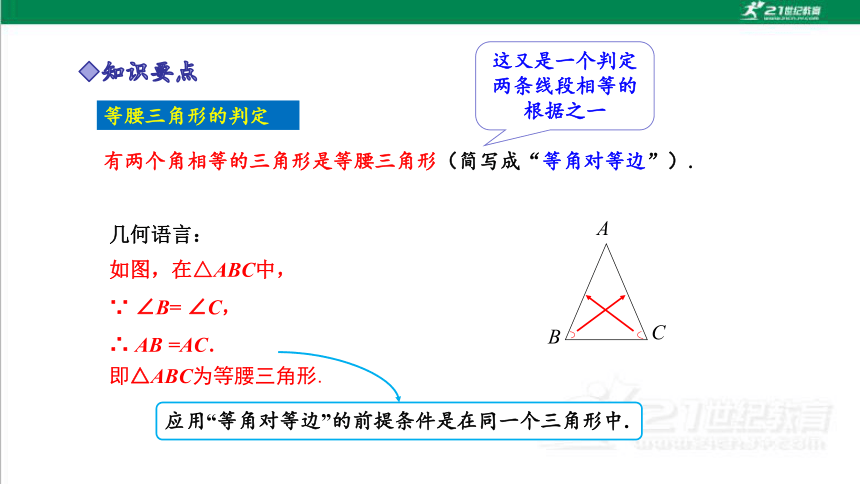
等腰三角形的判定
有两个角相等的三角形是等腰三角形(简写成“等角对等边”).
几何语言:
如图,在△ABC中,
∵ ∠B= ∠C,
∴ AB =AC.
A
B
C
应用“等角对等边”的前提条件是在同一个三角形中.
这又是一个判定两条线段相等的根据之一
即△ABC为等腰三角形.
A
B
C
D
2
1
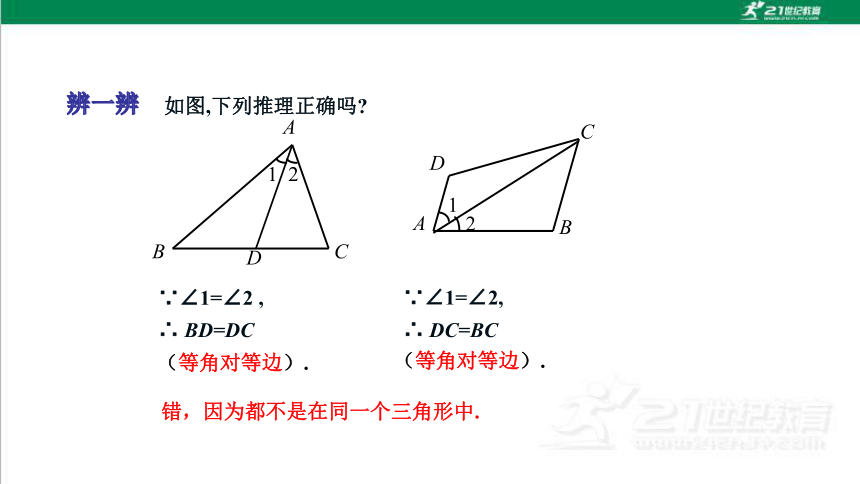
∵∠1=∠2 , ∴ BD=DC
(等角对等边).
∵∠1=∠2, ∴ DC=BC
A
B
C
D
2
1
(等角对等边).
错,因为都不是在同一个三角形中.
如图,下列推理正确吗
“等边对等角”与“等角对等边”的区别:
等腰三角形的性质:
两边相等 这两边所对的角相等(等边对等角)
等腰三角形的判定:
两角相等 这两角所对的边相等(等角对等边)
例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
分析:要证明AB=AC,可先证明∠B=∠C.因为∠1=∠2.所以可以设法找出∠B,∠C与∠1,∠2的关系.
已知:如图,AD是△ABC的外角∠CAE的平分线,AD//BC.
求证:AB=AC.
E
1
2
证明:∵AD//BC,
∴∠1=∠B,(两直线平行,同位角相等)
∠2=∠C.(两直线平行,内错角相等)
又AD平分∠CAE,
∴∠1=∠2,∴∠B=∠C,
∴AB=AC.(等角对等边).
E
1
2
AB//CD,∠1=∠2
∠1= ∠B, ∠2= ∠C
∠B= ∠C
AB= AC
如图,已知OC是∠AOB的平分线,CD//OB交OA于点D.
求证:△DOC是等腰三角形.
证明:∵OC平分∠AOB,
∴∠AOC=∠BOC,
∵CD∥OB,
∴∠DCO=∠BOC,
∴∠AOC=∠DCO,
∴OD=CD,
∴△DOC是等腰三角形.
角平分线+平行线可以推出等腰三角形.
解:∵在△ABC中,∠A=36°,∠C=72°,
∴∠ABC=72°.
∵∠DBC=36°,∴∠2=∠ABC-∠DBC=36°.
∴∠1=∠A+∠2=72°,
∴∠A=∠2,∠ABC=∠C=∠1,
∴AD=BD=BC,AB=AC.
图中的等腰三角形有△ABC,△ABD,△BCD.
1. 如图,∠A=36°,∠DBC=36°,∠C=72°,分别计算∠1,∠2的度数,并说明图中有哪些等腰三角形.
2
1
D
B
作法:如图.
(1)作线段AB=a.
(2)作线段AB的垂直平分线MN,
与AB相交于点D.
(3)在MN上取一点C,使得DC=h.
(4)连接AC,BC.
则△ABC就是所求作的等腰三角形.
例2 尺规作图:已知等腰三角形的底边长为a,底边上的高的长为h,求作这个等腰三角形.
a
h
A
B
C
D
M
N
等角对等边
注意是在同一个三角形中
有两个角相等的三角形是等腰三角形
定义
1.在△ABC中, 已知∠A=50°,∠B=65°,判断△ABC是什么三角形,为什么
△ABC是等腰三角形, 因为∠B=65°, ∠A=50°, 所以∠C=65°, ∠B =∠C=65°,所以△ABC是等腰三角形.
2.一个三角形的一个外角为130°,且它恰好等于一个不相邻的内角的2倍,这个三角形是( )
A.钝角三角形 B.直角三角形 C.等腰三角形 D.等边三角形
C
1
3.如图,直线a、b相交于点O,∠1=50°,点A在直线a上,直线b上存在点B,使以点O、A、B为顶点的三角形是等腰三角形,这样的B点有( )
A.1个 B.2个 C.3个 D.4个
O
a
b
D
A
4.如图,把一张长方形的纸沿着对角线折叠,重合部分是一个等腰三角形吗?为什么?
B
C
A
D
E
是
由折叠可知,∠EBD=∠CBD.
∵AD∥BC,∴∠EDB=∠CBD,
∴∠EDB=∠EBD,
∴BE=DE,△EBD是等腰三角形.
5.在△ABC中,AB=AC,倘若不留神,它的一部分被墨水涂没了,只留下一条底边BC和一个底角∠C,请问,有没有办法把原来的等腰三角形画出来?
A
B
C
3种“补出”方法:
方法1:量出∠C度数,画出∠B=∠C, ∠B与∠C的边相交得到顶点A.
方法2:作BC边上的中垂线,与∠C的一边相交得到顶点A.
方法3:对折.
难点
重点
理解和运用等腰三角形的判定定理.
1.掌握等腰三角形的判定定理.
2.能运“等腰三角形的判定定理”进行证明和计算.
3.培养论证几何图形问题的能力,体会证明的必要性.
探索并掌握等腰三角形的判定的过程,并用以解决实际问题.
1.等腰三角形是怎样定义的?
有两条边相等的三角形,叫作等腰三角形.
①等腰三角形是轴对称图形.
③等腰三角形底边上的中线、高及顶角平分线重合(简写成“三线合一”).
②等腰三角形的两个底角相等(简写成“等边对等角”) .
2.等腰三角形有哪些性质?
既是性质又是判定
A
B
C
D
思考 我们知道,如果一个三角形有两条边相等,那么它们所对的角相等. 反过来,如果一个三角形有两个角相等,那么它们所对的边有什么关系?
猜想 如果一个三角形有两个角相等,那么它们所对的边相等.
你能证明这个结论吗?
已知:如图,在△ABC中,∠B=∠C.
求证:AB=AC.
如图,作△ABC的角平分线AD.
在△ABD和△ACD中,
∠B=∠C,
∠BAD=∠CAD,
AD=AD,
∴△ABD≌△ACD(AAS).
∴ AB=AC.
证明:
A
C
B
D
你能得到什么结论呢?
等腰三角形的判定
有两个角相等的三角形是等腰三角形(简写成“等角对等边”).
几何语言:
如图,在△ABC中,
∵ ∠B= ∠C,
∴ AB =AC.
A
B
C
应用“等角对等边”的前提条件是在同一个三角形中.
这又是一个判定两条线段相等的根据之一
即△ABC为等腰三角形.
A
B
C
D
2
1
∵∠1=∠2 , ∴ BD=DC
(等角对等边).
∵∠1=∠2, ∴ DC=BC
A
B
C
D
2
1
(等角对等边).
错,因为都不是在同一个三角形中.
如图,下列推理正确吗
“等边对等角”与“等角对等边”的区别:
等腰三角形的性质:
两边相等 这两边所对的角相等(等边对等角)
等腰三角形的判定:
两角相等 这两角所对的边相等(等角对等边)
例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
分析:要证明AB=AC,可先证明∠B=∠C.因为∠1=∠2.所以可以设法找出∠B,∠C与∠1,∠2的关系.
已知:如图,AD是△ABC的外角∠CAE的平分线,AD//BC.
求证:AB=AC.
E
1
2
证明:∵AD//BC,
∴∠1=∠B,(两直线平行,同位角相等)
∠2=∠C.(两直线平行,内错角相等)
又AD平分∠CAE,
∴∠1=∠2,∴∠B=∠C,
∴AB=AC.(等角对等边).
E
1
2
AB//CD,∠1=∠2
∠1= ∠B, ∠2= ∠C
∠B= ∠C
AB= AC
如图,已知OC是∠AOB的平分线,CD//OB交OA于点D.
求证:△DOC是等腰三角形.
证明:∵OC平分∠AOB,
∴∠AOC=∠BOC,
∵CD∥OB,
∴∠DCO=∠BOC,
∴∠AOC=∠DCO,
∴OD=CD,
∴△DOC是等腰三角形.
角平分线+平行线可以推出等腰三角形.
解:∵在△ABC中,∠A=36°,∠C=72°,
∴∠ABC=72°.
∵∠DBC=36°,∴∠2=∠ABC-∠DBC=36°.
∴∠1=∠A+∠2=72°,
∴∠A=∠2,∠ABC=∠C=∠1,
∴AD=BD=BC,AB=AC.
图中的等腰三角形有△ABC,△ABD,△BCD.
1. 如图,∠A=36°,∠DBC=36°,∠C=72°,分别计算∠1,∠2的度数,并说明图中有哪些等腰三角形.
2
1
D
B
作法:如图.
(1)作线段AB=a.
(2)作线段AB的垂直平分线MN,
与AB相交于点D.
(3)在MN上取一点C,使得DC=h.
(4)连接AC,BC.
则△ABC就是所求作的等腰三角形.
例2 尺规作图:已知等腰三角形的底边长为a,底边上的高的长为h,求作这个等腰三角形.
a
h
A
B
C
D
M
N
等角对等边
注意是在同一个三角形中
有两个角相等的三角形是等腰三角形
定义
1.在△ABC中, 已知∠A=50°,∠B=65°,判断△ABC是什么三角形,为什么
△ABC是等腰三角形, 因为∠B=65°, ∠A=50°, 所以∠C=65°, ∠B =∠C=65°,所以△ABC是等腰三角形.
2.一个三角形的一个外角为130°,且它恰好等于一个不相邻的内角的2倍,这个三角形是( )
A.钝角三角形 B.直角三角形 C.等腰三角形 D.等边三角形
C
1
3.如图,直线a、b相交于点O,∠1=50°,点A在直线a上,直线b上存在点B,使以点O、A、B为顶点的三角形是等腰三角形,这样的B点有( )
A.1个 B.2个 C.3个 D.4个
O
a
b
D
A
4.如图,把一张长方形的纸沿着对角线折叠,重合部分是一个等腰三角形吗?为什么?
B
C
A
D
E
是
由折叠可知,∠EBD=∠CBD.
∵AD∥BC,∴∠EDB=∠CBD,
∴∠EDB=∠EBD,
∴BE=DE,△EBD是等腰三角形.
5.在△ABC中,AB=AC,倘若不留神,它的一部分被墨水涂没了,只留下一条底边BC和一个底角∠C,请问,有没有办法把原来的等腰三角形画出来?
A
B
C
3种“补出”方法:
方法1:量出∠C度数,画出∠B=∠C, ∠B与∠C的边相交得到顶点A.
方法2:作BC边上的中垂线,与∠C的一边相交得到顶点A.
方法3:对折.
同课章节目录
