人教版八年级数学上册第16章整式的乘法16.2整式的乘法第2课时单项式与多项式相乘 课件(共16张PPT)
文档属性
| 名称 | 人教版八年级数学上册第16章整式的乘法16.2整式的乘法第2课时单项式与多项式相乘 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 655.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 05:19:10 | ||
图片预览




文档简介
(共16张PPT)
1.探索单项式与多项式相乘的法则.
2.会运用单项式与多项式相乘的法则进行计算.
难点
重点
探索单项式与多项式相乘的运算法则.
单项式与多项式相乘的运算法则的应用.
单项式与单项式的乘法法则
单项式与单项式相乘,把它们的系数、同底数幂分别相乘作为积的因式,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
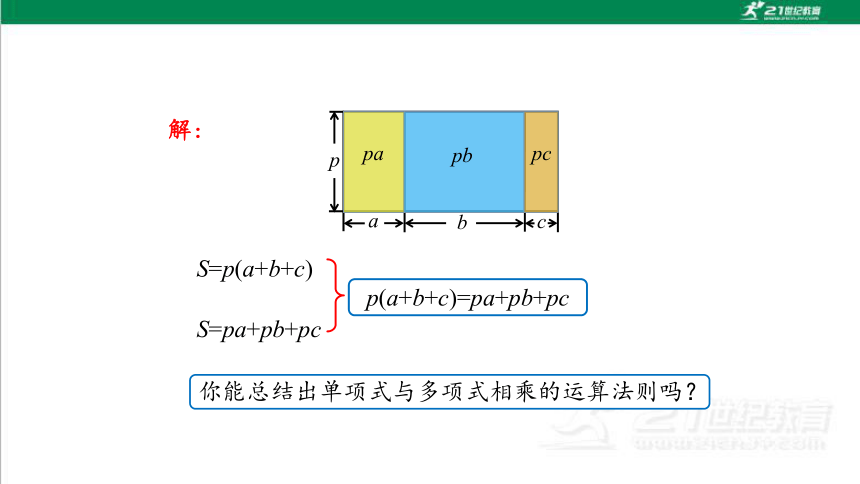
(引言中的问题)为了扩大绿地面积,要把街心花园的一块长为p m,宽为b m的长方形绿地,向两边分别加宽a m和c m,你能用几种方法表示扩大后的绿地面积?不同的表示方法之间有什么关系?
a
b
c
p
a
b
c
p
S=p(a+b+c)
S=pa+pb+pc
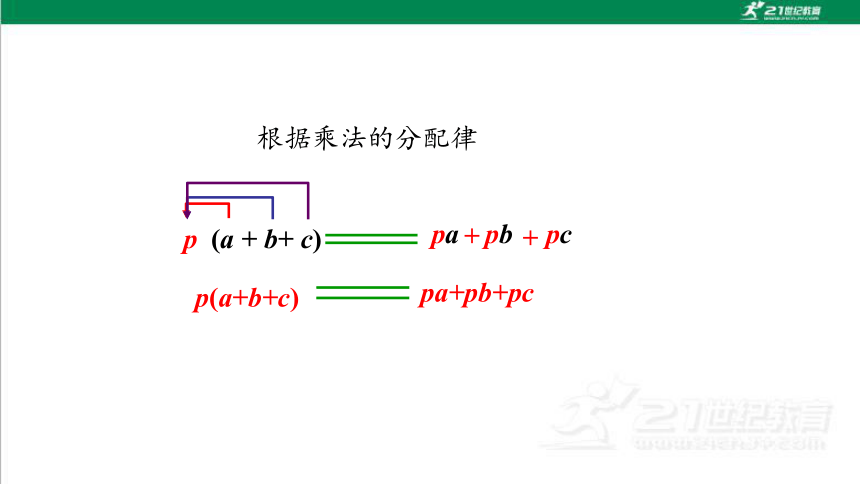
p(a+b+c)=pa+pb+pc
你能总结出单项式与多项式相乘的运算法则吗?
pa
pb
pc
解:
pa+pb+pc
p(a+b+c)
p (a + b+ c)
pb
+
pc
pa
+
根据乘法的分配律
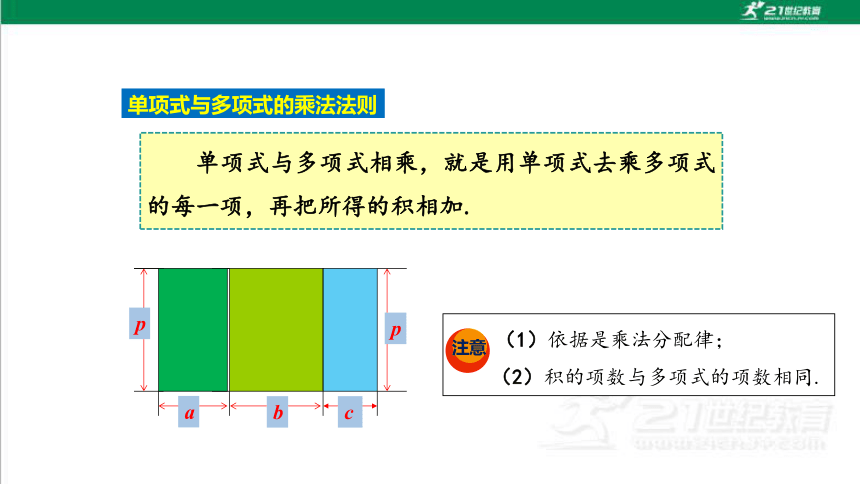
单项式与多项式的乘法法则
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
(1)依据是乘法分配律;
(2)积的项数与多项式的项数相同.
注意
m
b
p
a
p
c
示例:
(-2x3y) ·(3xy2-3xy +1)=-2x3y·3xy2+(-2x3y) ·(-3xy)+(-2x3y) ·1
=-6x4y3+6x4y2-2x3y
单项式分别乘多项式的每一项
例2 计算:
(1)(-4x2)·(3x+1);
解:(-4x2)·(3x+1)
=
=-12x3-4x2;
(-4x2)·(3x)
(-4x2)·1
+
=(-4×3)(x2·x)+(-4x2)
解:原式
(3)(x-3y)(xy2)2;
解:(x-3y)(xy2)2
=(x-3y)·x2y4
=x·x2y4+(-3y)·x2y4
=x3y4-3x2y5;
(4)x(y-z)-y(z-x)+z(x-y).
解:x(y-z)-y(z-x)+z(x-y)
=xy+x(-z)+(-y)z+(-y)(-x)+zx+z(-y)
=xy-xz-yz+yx+zx-zy
=2xy-2yz.
单项式与多项式相乘
乘法分配律
转化
单项式与单项式相乘
整式的乘法
单项式×
多项式
实质上是转化为单项式×单项式
四点注意
(1)注意符号,多项式中每一项都包括它前面的符号
(2)不要出现漏乘现象 (3)运算顺序:先乘方,再乘除,最后加减
(4)对于混合运算,注意最后应合并同类项
1. 单项式与多项式相乘,就是用单项式去乘多项式的________,再把所得的积________.
2. 4(a-b+1)=___________________.
每一项
相加
4a-4b+4
3. 3x(2x-y2)=___________________.
6x2-3xy2
4.(2x-5y+6z)(-3x) =___________________.
-6x2+15xy-18xz
5. (-2a2)2(-a-2b+c)=___________________.
-4a5-8a4b+4a4c
6. 计算:-2x2·(xy+y2)-5x(x2y-xy2).
(1)将2x2与5x前面的“-”看成性质符号;
(2)单项式与多项式相乘的结果中, 应将同类项合并.
注意
解:原式=( -2x2) ·xy+(-2x2) ·y2+(-5x) ·x2y+(-5x) ·(-xy2)
=-2x3 y+(-2x2y2)+(-5x3y)+5x2y2
=-7x3 y+3x2y2.
住宅用地
人民广场
商业用地
3a
3a+2b
2a-b
4a
7. 如图,一块长方形地用来建造住宅、广场、商厦,求这块地的面积.
解:4a[(3a+2b)+(2a-b)]
=4a(5a+b)
=4a·5a+4a·b
=20a2+4ab.
答:这块地的面积为20a2+4ab.
1.探索单项式与多项式相乘的法则.
2.会运用单项式与多项式相乘的法则进行计算.
难点
重点
探索单项式与多项式相乘的运算法则.
单项式与多项式相乘的运算法则的应用.
单项式与单项式的乘法法则
单项式与单项式相乘,把它们的系数、同底数幂分别相乘作为积的因式,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
(引言中的问题)为了扩大绿地面积,要把街心花园的一块长为p m,宽为b m的长方形绿地,向两边分别加宽a m和c m,你能用几种方法表示扩大后的绿地面积?不同的表示方法之间有什么关系?
a
b
c
p
a
b
c
p
S=p(a+b+c)
S=pa+pb+pc
p(a+b+c)=pa+pb+pc
你能总结出单项式与多项式相乘的运算法则吗?
pa
pb
pc
解:
pa+pb+pc
p(a+b+c)
p (a + b+ c)
pb
+
pc
pa
+
根据乘法的分配律
单项式与多项式的乘法法则
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
(1)依据是乘法分配律;
(2)积的项数与多项式的项数相同.
注意
m
b
p
a
p
c
示例:
(-2x3y) ·(3xy2-3xy +1)=-2x3y·3xy2+(-2x3y) ·(-3xy)+(-2x3y) ·1
=-6x4y3+6x4y2-2x3y
单项式分别乘多项式的每一项
例2 计算:
(1)(-4x2)·(3x+1);
解:(-4x2)·(3x+1)
=
=-12x3-4x2;
(-4x2)·(3x)
(-4x2)·1
+
=(-4×3)(x2·x)+(-4x2)
解:原式
(3)(x-3y)(xy2)2;
解:(x-3y)(xy2)2
=(x-3y)·x2y4
=x·x2y4+(-3y)·x2y4
=x3y4-3x2y5;
(4)x(y-z)-y(z-x)+z(x-y).
解:x(y-z)-y(z-x)+z(x-y)
=xy+x(-z)+(-y)z+(-y)(-x)+zx+z(-y)
=xy-xz-yz+yx+zx-zy
=2xy-2yz.
单项式与多项式相乘
乘法分配律
转化
单项式与单项式相乘
整式的乘法
单项式×
多项式
实质上是转化为单项式×单项式
四点注意
(1)注意符号,多项式中每一项都包括它前面的符号
(2)不要出现漏乘现象 (3)运算顺序:先乘方,再乘除,最后加减
(4)对于混合运算,注意最后应合并同类项
1. 单项式与多项式相乘,就是用单项式去乘多项式的________,再把所得的积________.
2. 4(a-b+1)=___________________.
每一项
相加
4a-4b+4
3. 3x(2x-y2)=___________________.
6x2-3xy2
4.(2x-5y+6z)(-3x) =___________________.
-6x2+15xy-18xz
5. (-2a2)2(-a-2b+c)=___________________.
-4a5-8a4b+4a4c
6. 计算:-2x2·(xy+y2)-5x(x2y-xy2).
(1)将2x2与5x前面的“-”看成性质符号;
(2)单项式与多项式相乘的结果中, 应将同类项合并.
注意
解:原式=( -2x2) ·xy+(-2x2) ·y2+(-5x) ·x2y+(-5x) ·(-xy2)
=-2x3 y+(-2x2y2)+(-5x3y)+5x2y2
=-7x3 y+3x2y2.
住宅用地
人民广场
商业用地
3a
3a+2b
2a-b
4a
7. 如图,一块长方形地用来建造住宅、广场、商厦,求这块地的面积.
解:4a[(3a+2b)+(2a-b)]
=4a(5a+b)
=4a·5a+4a·b
=20a2+4ab.
答:这块地的面积为20a2+4ab.
同课章节目录
