人教版八年级数学上册第15章轴对称15.3.2等边三角形第1课时等边三角形的性质与判定 课件(共20张PPT)
文档属性
| 名称 | 人教版八年级数学上册第15章轴对称15.3.2等边三角形第1课时等边三角形的性质与判定 课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 18.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 05:33:30 | ||
图片预览




文档简介
(共20张PPT)
难点
重点
掌握等边三角形的性质和判定.
1.探索等边三角形的性质和判定.
2.能运用等边三角形的性质和判定进行计算和证明.
探索并掌握等边三角形性质的证明过程,熟练地运用等边三角形的性质解决问题.
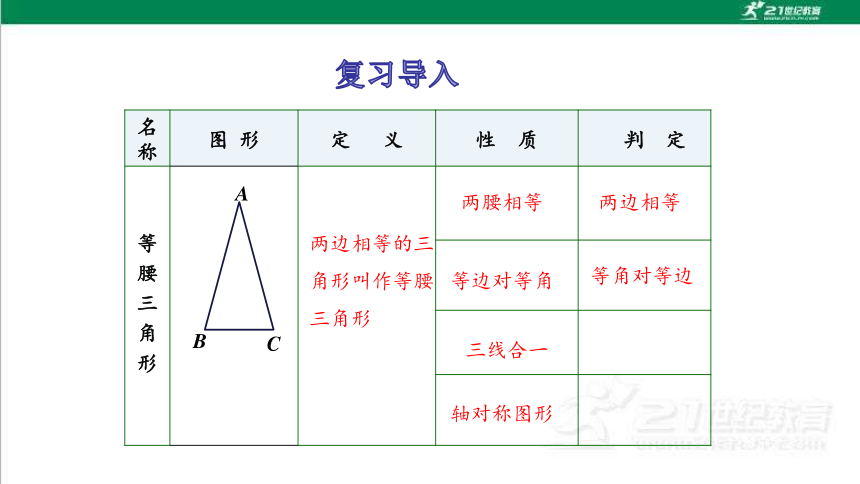
名称 图 形 定 义 性 质 判 定
等
腰
三
角
形
等边对等角
三线合一
等角对等边
两边相等
两腰相等
轴对称图形
A
B
C
两边相等的三角形叫作等腰三角形
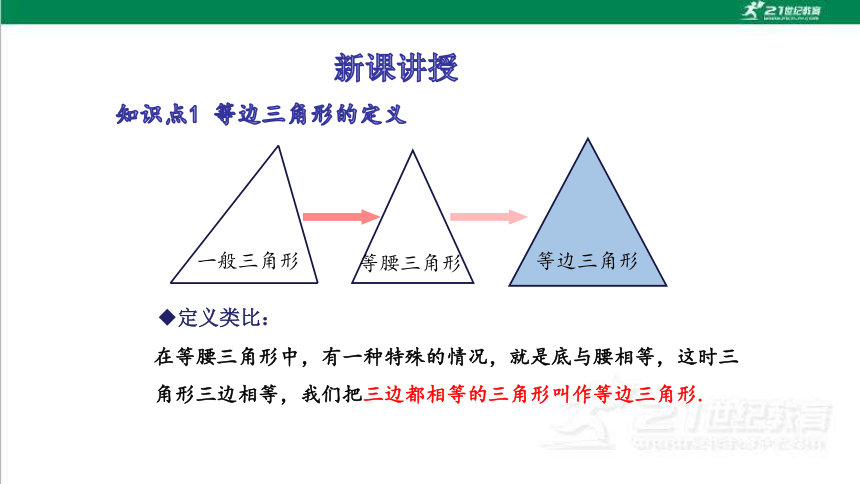
等腰三角形
等边三角形
一般三角形
定义类比:
在等腰三角形中,有一种特殊的情况,就是底与腰相等,这时三角形三边相等,我们把三边都相等的三角形叫作等边三角形.
A
B
C
A
B
C
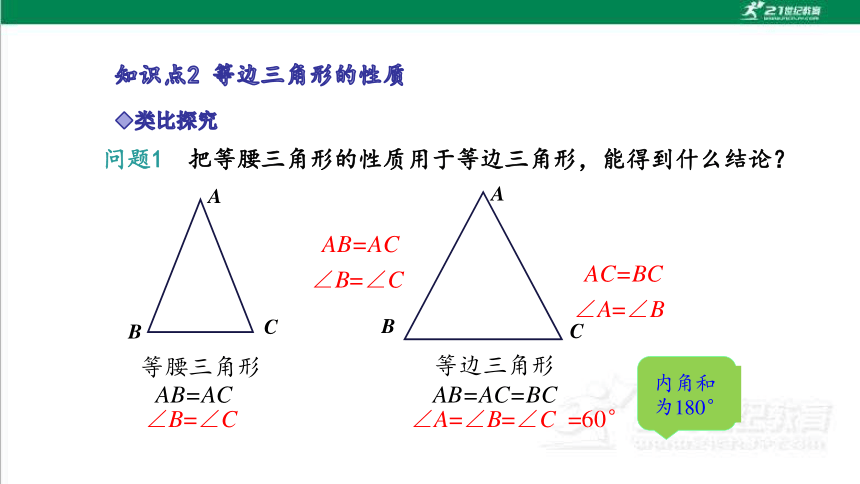
问题1 把等腰三角形的性质用于等边三角形,能得到什么结论?
等腰三角形
AB=AC
∠B=∠C
等边三角形
AB=AC=BC
AB=AC
∠B=∠C
AC=BC
∠A=∠B
∠A=∠B=∠C
=60°
结论:等边三角形的三个角都相等,并且每一个角都等于60°.
证明: 已知:AB=AC=BC ,
求证:∠A=∠B=∠C= 60°.
证明: ∵AB=AC,
∴∠B=∠C .(等边对等角)
同理,∠A=∠C .
∴∠A=∠B=∠C.
∵ ∠A+∠B+∠C=180°,
∴ ∠A=∠B=∠C=60 °.
A
B
C
A
B
C
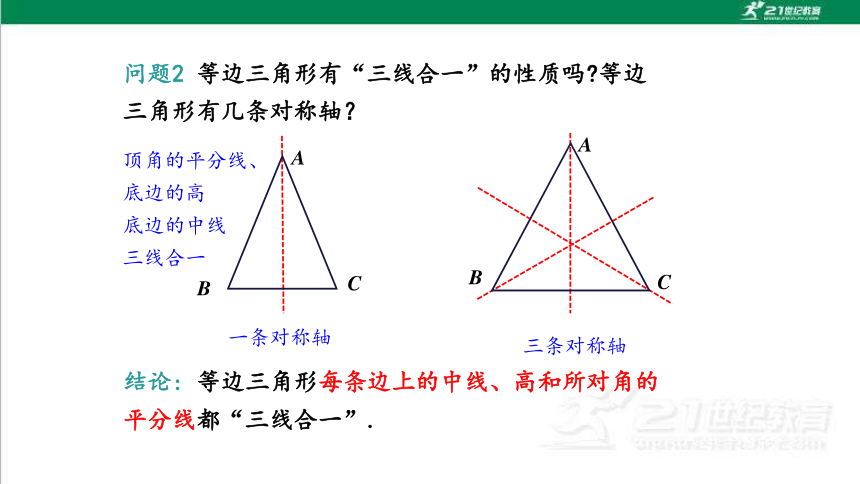
问题2 等边三角形有“三线合一”的性质吗 等边三角形有几条对称轴?
结论: 等边三角形每条边上的中线、高和所对角的平分线都“三线合一”.
顶角的平分线、底边的高
底边的中线
三线合一
一条对称轴
三条对称轴
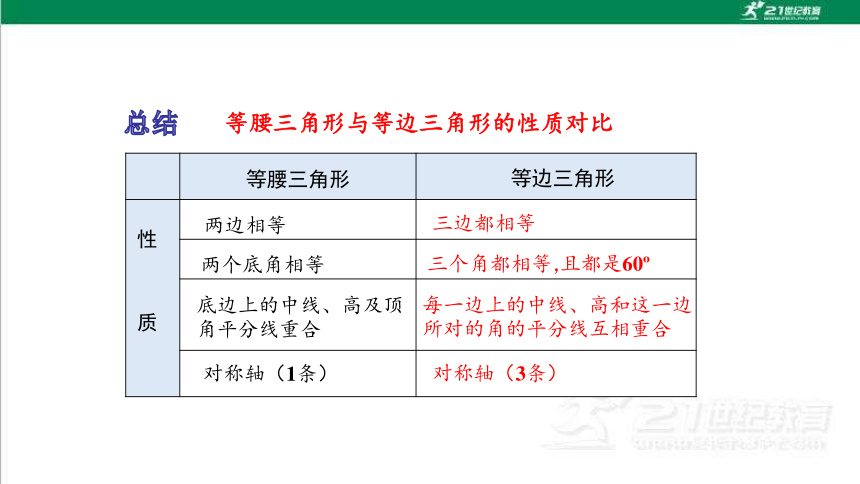
等腰三角形与等边三角形的性质对比
等腰三角形
性 质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高及顶角平分线重合
且都是60
两边相等
三边都相等
A
C
B
D
E
例1 如图,△ABC和△ADE都是等边三角形,已知△ABC的周长为18cm,EC =2cm,则△ADE的周长是 cm.
12
例2 如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.
解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=60°-40°=20°.
∵BE=DE,
∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.
方法总结:等边三角形是特殊的三角形,它的三个角都是60°,这个性质常应用在求三角形角度的问题上,一般需结合“等边对等角”、三角形的内角和与外角的性质、全等三角形的性质等.
类比等腰三角形的判定方法
等腰三角形
判 定
三个角都相等的三角形是等边三角形
等边三角形
从角看:有两个角相等的三角形是等腰三角形
从边看:两边相等的三角形是等腰三角形
三边都相等的三角形是等边三角形
(1)
(2)
(6)
(5)
不
是
是
是
是
是
(4)
(3)
不一定
是
例3 如图,△ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A=∠B=∠C.
∵ DE//BC,
∴ ∠ADE=∠B, ∠AED=∠C.
∴ ∠A=∠ADE=∠AED.
∴ △ADE是等边三角形.
想一想:本题还有其他证法吗?
上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗 试说明理由.
A
C
B
D
E
如图,在等边三角形ABC中,AD=AE, 求证:△ADE是等边三角形.
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ AD=AE,
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
定义
底=腰
特殊性
性质
特殊性
边
三边相等
角
三个角都等于60 °
轴对称性
轴对称图形,每条边上都具有“三线合一”性质
判定
特殊性
三边法
三角法
等腰三角形法
1. 已知△ABC中,∠A=∠B=60°,AB=3cm,则△ABC的周长为______cm.
9
2.等边三角形的两条高线相交成钝角的度数是______°.
120
3.如图,等边三角形ABC的三条角平分线交于点O,DE∥BC,则这个图形中的等腰三角形共有( )
A. 4个 B. 5个
C. 6个 D. 7个
D
A
C
B
D
E
O
B
C
D
A
E
4.如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,求∠EDA的度数.
解:
∵ △ABC是等边三角形,
∴∠CBA=60°.
∵BD是AC边上的中线,
∴∠BDA=90°, ∠DBA=30 °.
∵ BD=BE,
∴ ∠BDE=(180 °- ∠DBA) ÷2 =(180°-30°) ÷2=75°.
∴ ∠EDA=90 °- ∠BDE=90°-75°=15°.
5.如图,A,O,D三点共线,△OAB和△OCD是两个全等的等边三角形,求∠AEB的大小.
C
B
O
D
A
E
解:
∵△OAB和△OCD是两个全等的等边三角形.
∴AO=BO,CO=DO, ∠AOB=∠COD=60°.
∵ A,O,D三点共线,
∴ ∠DOB=∠COA=120°,
∴ △COA ≌△DOB(SAS).
∴ ∠DBO=∠CAO.
设OB与EA相交于点F,
∵ ∠EFB=∠AFO,
∴ ∠AEB=∠AOB=60°.
F
难点
重点
掌握等边三角形的性质和判定.
1.探索等边三角形的性质和判定.
2.能运用等边三角形的性质和判定进行计算和证明.
探索并掌握等边三角形性质的证明过程,熟练地运用等边三角形的性质解决问题.
名称 图 形 定 义 性 质 判 定
等
腰
三
角
形
等边对等角
三线合一
等角对等边
两边相等
两腰相等
轴对称图形
A
B
C
两边相等的三角形叫作等腰三角形
等腰三角形
等边三角形
一般三角形
定义类比:
在等腰三角形中,有一种特殊的情况,就是底与腰相等,这时三角形三边相等,我们把三边都相等的三角形叫作等边三角形.
A
B
C
A
B
C
问题1 把等腰三角形的性质用于等边三角形,能得到什么结论?
等腰三角形
AB=AC
∠B=∠C
等边三角形
AB=AC=BC
AB=AC
∠B=∠C
AC=BC
∠A=∠B
∠A=∠B=∠C
=60°
结论:等边三角形的三个角都相等,并且每一个角都等于60°.
证明: 已知:AB=AC=BC ,
求证:∠A=∠B=∠C= 60°.
证明: ∵AB=AC,
∴∠B=∠C .(等边对等角)
同理,∠A=∠C .
∴∠A=∠B=∠C.
∵ ∠A+∠B+∠C=180°,
∴ ∠A=∠B=∠C=60 °.
A
B
C
A
B
C
问题2 等边三角形有“三线合一”的性质吗 等边三角形有几条对称轴?
结论: 等边三角形每条边上的中线、高和所对角的平分线都“三线合一”.
顶角的平分线、底边的高
底边的中线
三线合一
一条对称轴
三条对称轴
等腰三角形与等边三角形的性质对比
等腰三角形
性 质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高及顶角平分线重合
且都是60
两边相等
三边都相等
A
C
B
D
E
例1 如图,△ABC和△ADE都是等边三角形,已知△ABC的周长为18cm,EC =2cm,则△ADE的周长是 cm.
12
例2 如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.
解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=60°-40°=20°.
∵BE=DE,
∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.
方法总结:等边三角形是特殊的三角形,它的三个角都是60°,这个性质常应用在求三角形角度的问题上,一般需结合“等边对等角”、三角形的内角和与外角的性质、全等三角形的性质等.
类比等腰三角形的判定方法
等腰三角形
判 定
三个角都相等的三角形是等边三角形
等边三角形
从角看:有两个角相等的三角形是等腰三角形
从边看:两边相等的三角形是等腰三角形
三边都相等的三角形是等边三角形
(1)
(2)
(6)
(5)
不
是
是
是
是
是
(4)
(3)
不一定
是
例3 如图,△ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A=∠B=∠C.
∵ DE//BC,
∴ ∠ADE=∠B, ∠AED=∠C.
∴ ∠A=∠ADE=∠AED.
∴ △ADE是等边三角形.
想一想:本题还有其他证法吗?
上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗 试说明理由.
A
C
B
D
E
如图,在等边三角形ABC中,AD=AE, 求证:△ADE是等边三角形.
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ AD=AE,
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
定义
底=腰
特殊性
性质
特殊性
边
三边相等
角
三个角都等于60 °
轴对称性
轴对称图形,每条边上都具有“三线合一”性质
判定
特殊性
三边法
三角法
等腰三角形法
1. 已知△ABC中,∠A=∠B=60°,AB=3cm,则△ABC的周长为______cm.
9
2.等边三角形的两条高线相交成钝角的度数是______°.
120
3.如图,等边三角形ABC的三条角平分线交于点O,DE∥BC,则这个图形中的等腰三角形共有( )
A. 4个 B. 5个
C. 6个 D. 7个
D
A
C
B
D
E
O
B
C
D
A
E
4.如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,求∠EDA的度数.
解:
∵ △ABC是等边三角形,
∴∠CBA=60°.
∵BD是AC边上的中线,
∴∠BDA=90°, ∠DBA=30 °.
∵ BD=BE,
∴ ∠BDE=(180 °- ∠DBA) ÷2 =(180°-30°) ÷2=75°.
∴ ∠EDA=90 °- ∠BDE=90°-75°=15°.
5.如图,A,O,D三点共线,△OAB和△OCD是两个全等的等边三角形,求∠AEB的大小.
C
B
O
D
A
E
解:
∵△OAB和△OCD是两个全等的等边三角形.
∴AO=BO,CO=DO, ∠AOB=∠COD=60°.
∵ A,O,D三点共线,
∴ ∠DOB=∠COA=120°,
∴ △COA ≌△DOB(SAS).
∴ ∠DBO=∠CAO.
设OB与EA相交于点F,
∵ ∠EFB=∠AFO,
∴ ∠AEB=∠AOB=60°.
F
同课章节目录
