16.3.2 完全平方公式 第1课时 完全平方公式 学案(含答案)2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 16.3.2 完全平方公式 第1课时 完全平方公式 学案(含答案)2025-2026学年数学人教版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 33.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 00:00:00 | ||
图片预览

文档简介
16.3.2 完全平方公式
第1课时 完全平方公式
学习目标
1.理解完全平方公式,能用公式进行计算.
2.在探索完全平方公式的过程中,感悟从具体到抽象地研究问题的方法,在验证完全平方公式的过程中,感知数形结合思想.
自主探索
问题 1 运用平方差公式计算:
(1)(2a+3b)(2a-3b);
(2)101×99.
问题 2 你能迅速算出1022的结果吗?992呢?
任务一 探究完全平方公式
活动1 计算下列多项式的积.
(1)(p+1)2=(p+1)(p+1)= ;
(2)(m+2)2=( )( )= ;
(3)(p-1)2=( )( )= ;
(4)(m-2)2=( )( )= .
思考:比较式子等号的左右两边,你发现什么规律了吗?
猜想:根据你发现的规律,能直接写出(a+b)2的计算结果吗?(a-b)2呢?你是怎么想的?
归纳总结:
(1)完全平方公式:
两个数的和(或差)的平方,等于它们的 ,加上(或减去)它们的积的 .
(a+b)2= ,(a-b)2= .
活动2 你能验证完全平方公式吗?有哪些验证方法?
(1)用多项式乘法证明
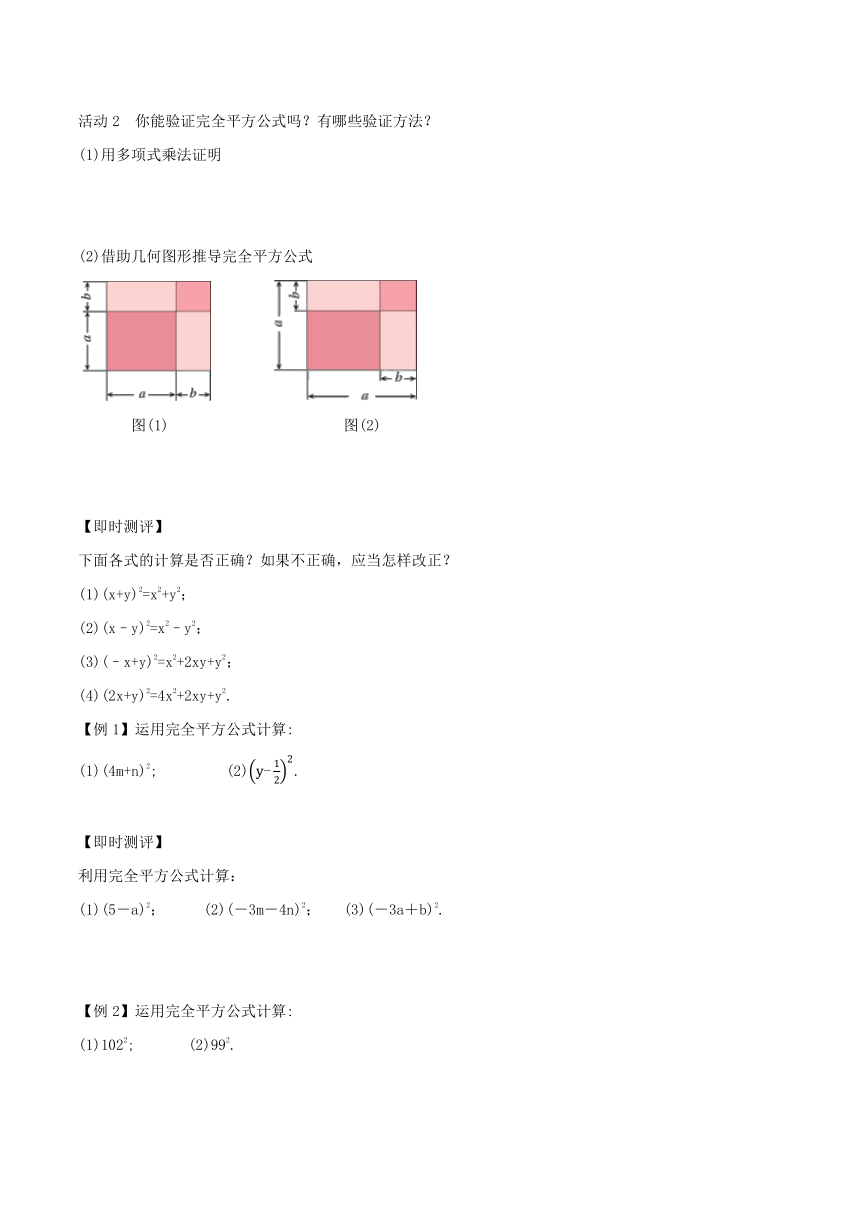
(2)借助几何图形推导完全平方公式
图(1) 图(2)
【即时测评】
下面各式的计算是否正确?如果不正确,应当怎样改正?
(1)(x+y)2=x2+y2;
(2)(x–y)2=x2–y2;
(3)(–x+y)2=x2+2xy+y2;
(4)(2x+y)2=4x2+2xy+y2.
【例1】运用完全平方公式计算:
(1)(4m+n)2; (2).
【即时测评】
利用完全平方公式计算:
(1)(5-a)2; (2)(-3m-4n)2; (3)(-3a+b)2.
【例2】运用完全平方公式计算:
(1)1022; (2)992.
思考
(1)(a+b)2=(-a-b)2相等吗?
(2)(a-b)2=(b-a)2相等吗?
当堂达标
1.计算(2x-y)2等于( )
A.4x2-4xy+y2 B.4x2-2xy+y2 C.4x2-y2 D.4x2+y2
2.将1052变形正确的是( )
A.1052=1002+52 B.1052=(100-5)(100+5)
C.1052=1002+2×100×5+52 D.1052=1002+100×5+52
3.若(3x-a)2=9x2-bx+16,则a+b的值为( )
A.28 B.-28 C.24或-24 D.28或-28
4.下列变形中:①(b-4c)2=b2-16c2;②(a-2bc)2=a2+4abc+4b2c2;③(x+y)2=x2+xy+y2;④(4m-n)2=16m2-8mn+n2.错误的是( )
A.①②③ B.①②④ C.①③④ D.②③④
5.计算:(1)(-2m-n)2;
(2)(2x+3y)(-2x-3y).
6.若a+b=5,ab=-6, 求a2+b2,a2-ab+b2.
课堂小结
1.什么是完全平方公式?公式中的 a 、 b 是只表示一个数吗?
2.完全平方公式的特点是什么?在运用公式过程中要注意什么?
3.你在这节课还有什么收获?
参考答案
当堂达标
1.A 2.C 3.D 4.A
5.解:(1)(-2m-n)2=[-(2m+n)]2=(2m+n)2
=(2m)2+2·2m·n+n2=4m2+4mn+n2.
(2)(2x+3y)(-2x-3y)=-(2x+3y)2=-[(2x)2+2·2x·3y+(3y)2]=-(4x2+12xy+9y2)=-4x2-12xy-9y2.
6.解:a2+b2=(a+b)2-2ab=52-2×(-6)=37;
a2-ab+b2=a2+b2-ab=37-(-6)=43.
第1课时 完全平方公式
学习目标
1.理解完全平方公式,能用公式进行计算.
2.在探索完全平方公式的过程中,感悟从具体到抽象地研究问题的方法,在验证完全平方公式的过程中,感知数形结合思想.
自主探索
问题 1 运用平方差公式计算:
(1)(2a+3b)(2a-3b);
(2)101×99.
问题 2 你能迅速算出1022的结果吗?992呢?
任务一 探究完全平方公式
活动1 计算下列多项式的积.
(1)(p+1)2=(p+1)(p+1)= ;
(2)(m+2)2=( )( )= ;
(3)(p-1)2=( )( )= ;
(4)(m-2)2=( )( )= .
思考:比较式子等号的左右两边,你发现什么规律了吗?
猜想:根据你发现的规律,能直接写出(a+b)2的计算结果吗?(a-b)2呢?你是怎么想的?
归纳总结:
(1)完全平方公式:
两个数的和(或差)的平方,等于它们的 ,加上(或减去)它们的积的 .
(a+b)2= ,(a-b)2= .
活动2 你能验证完全平方公式吗?有哪些验证方法?
(1)用多项式乘法证明
(2)借助几何图形推导完全平方公式
图(1) 图(2)
【即时测评】
下面各式的计算是否正确?如果不正确,应当怎样改正?
(1)(x+y)2=x2+y2;
(2)(x–y)2=x2–y2;
(3)(–x+y)2=x2+2xy+y2;
(4)(2x+y)2=4x2+2xy+y2.
【例1】运用完全平方公式计算:
(1)(4m+n)2; (2).
【即时测评】
利用完全平方公式计算:
(1)(5-a)2; (2)(-3m-4n)2; (3)(-3a+b)2.
【例2】运用完全平方公式计算:
(1)1022; (2)992.
思考
(1)(a+b)2=(-a-b)2相等吗?
(2)(a-b)2=(b-a)2相等吗?
当堂达标
1.计算(2x-y)2等于( )
A.4x2-4xy+y2 B.4x2-2xy+y2 C.4x2-y2 D.4x2+y2
2.将1052变形正确的是( )
A.1052=1002+52 B.1052=(100-5)(100+5)
C.1052=1002+2×100×5+52 D.1052=1002+100×5+52
3.若(3x-a)2=9x2-bx+16,则a+b的值为( )
A.28 B.-28 C.24或-24 D.28或-28
4.下列变形中:①(b-4c)2=b2-16c2;②(a-2bc)2=a2+4abc+4b2c2;③(x+y)2=x2+xy+y2;④(4m-n)2=16m2-8mn+n2.错误的是( )
A.①②③ B.①②④ C.①③④ D.②③④
5.计算:(1)(-2m-n)2;
(2)(2x+3y)(-2x-3y).
6.若a+b=5,ab=-6, 求a2+b2,a2-ab+b2.
课堂小结
1.什么是完全平方公式?公式中的 a 、 b 是只表示一个数吗?
2.完全平方公式的特点是什么?在运用公式过程中要注意什么?
3.你在这节课还有什么收获?
参考答案
当堂达标
1.A 2.C 3.D 4.A
5.解:(1)(-2m-n)2=[-(2m+n)]2=(2m+n)2
=(2m)2+2·2m·n+n2=4m2+4mn+n2.
(2)(2x+3y)(-2x-3y)=-(2x+3y)2=-[(2x)2+2·2x·3y+(3y)2]=-(4x2+12xy+9y2)=-4x2-12xy-9y2.
6.解:a2+b2=(a+b)2-2ab=52-2×(-6)=37;
a2-ab+b2=a2+b2-ab=37-(-6)=43.
同课章节目录
