22.3 实际问题与二次函数 同步练习(含答案)
文档属性
| 名称 | 22.3 实际问题与二次函数 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 21:29:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
22.3 实际问题与二次函数
一、单选题
1.(2025九下·河西开学考)一名男生推铅球,铅球出手时,铅球的高度为.铅球行进的高度(单位:)是水平距离(单位:)的二次函数,与之间的函数关系式为.有下列结论:
①从铅球出手到落地时水平距离为;
②铅球行进过程中的高度可以达到;
③铅球从出手到飞行至最高点的水平距离小于从最高点运动至落地的水平距离.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
2.(2023九上·集美期中)据省统计局公布的数据,合肥市2023年第一季度总值约为2.6千亿元人民币,若我市第三季度总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )
A. B.
C. D.
3.(2023九上·徐州期中)图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面,水面宽,如图(2)建立平面直角坐标系,则抛物线的关系式是( )
A. B. C. D.
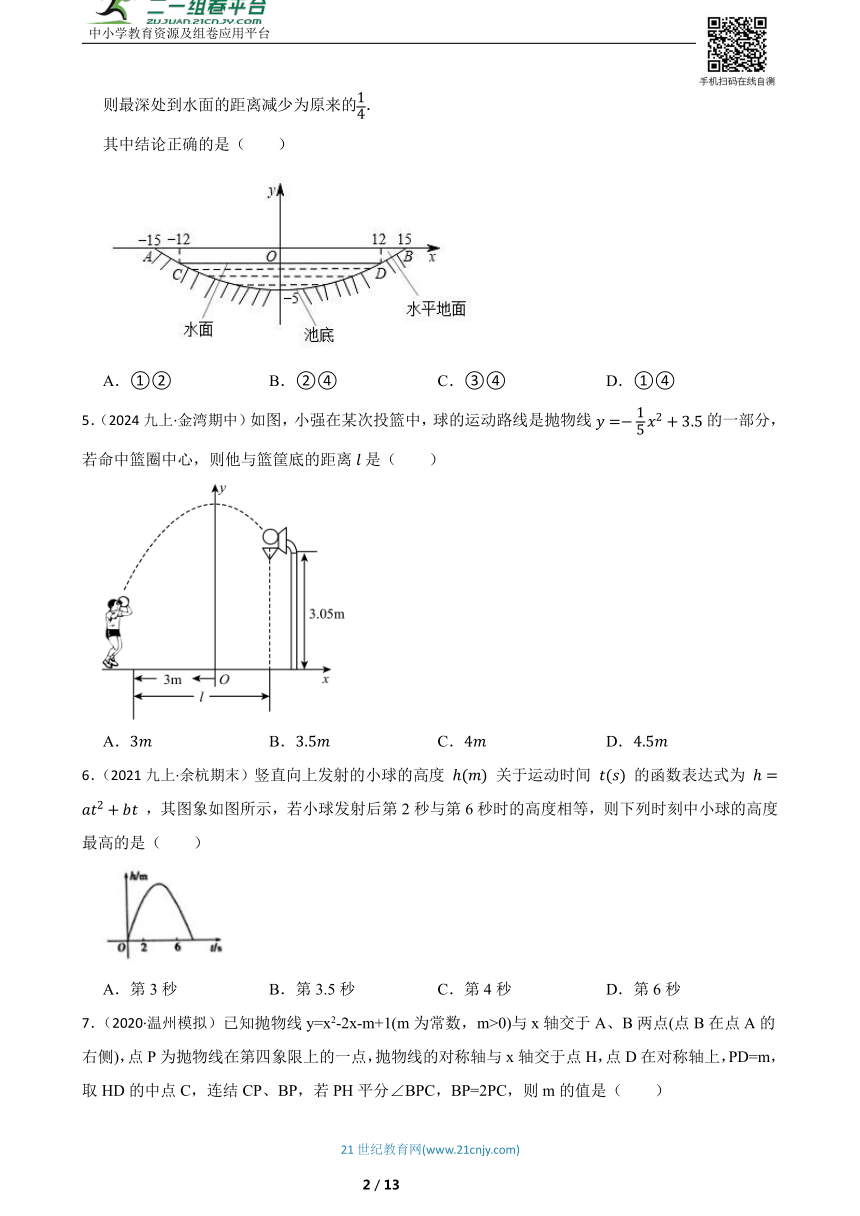
4.(2023九下·天山模拟)某池塘的截面如图所示,池底呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:m).有下列结论:
①;
②池底所在抛物线的解析式为;
③池塘最深处到水面CD的距离为1.8m;
④若池塘中水面的宽度减少为原来的一半,
则最深处到水面的距离减少为原来的.
其中结论正确的是( )
A.①② B.②④ C.③④ D.①④
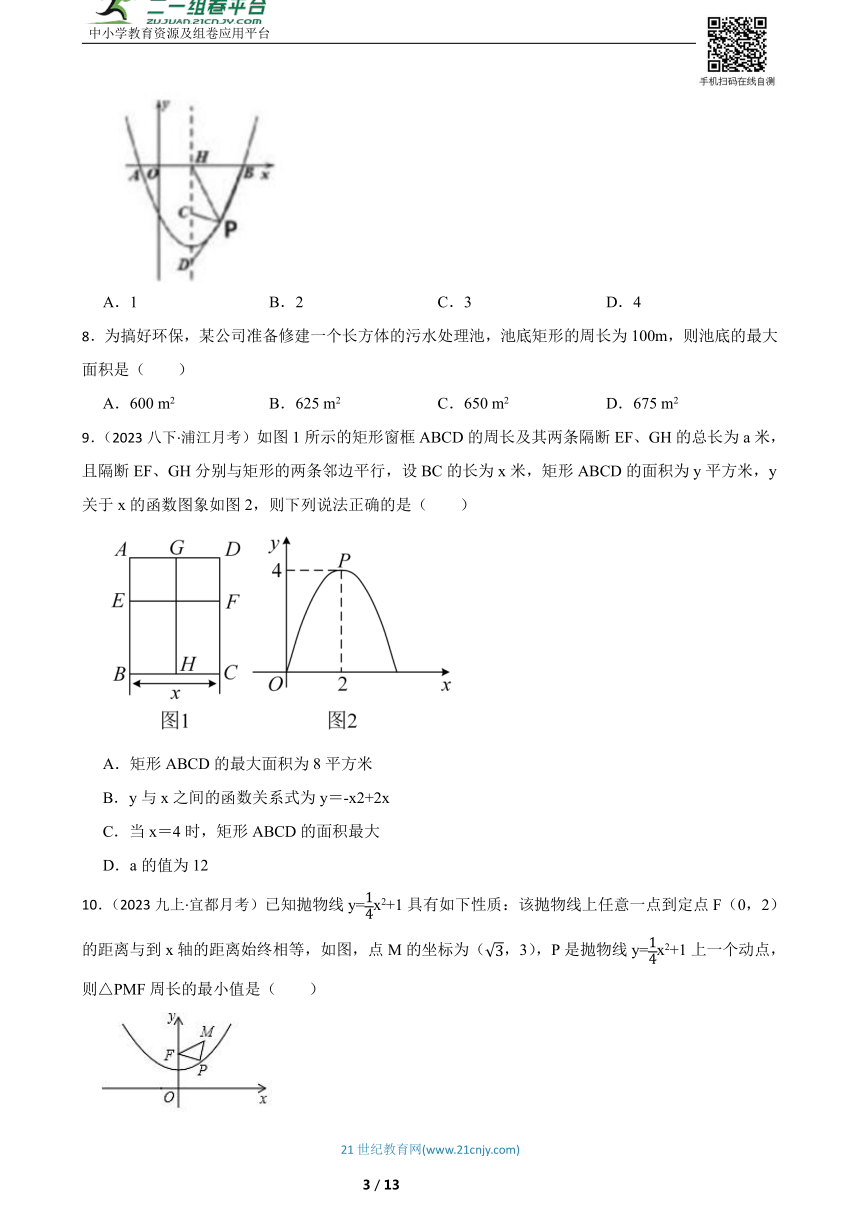
5.(2024九上·金湾期中)如图,小强在某次投篮中,球的运动路线是抛物线的一部分,若命中篮圈中心,则他与篮筐底的距离是( )
A. B. C. D.
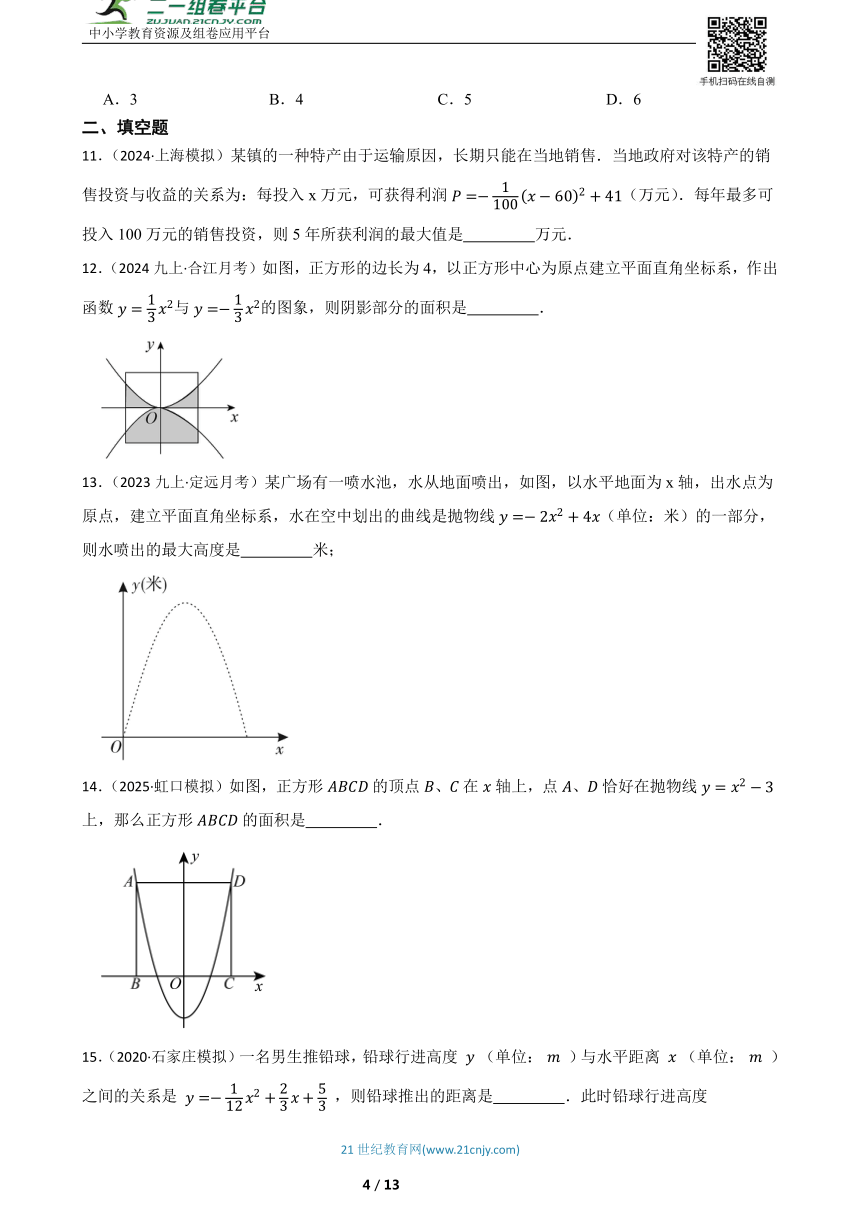
6.(2021九上·余杭期末)竖直向上发射的小球的高度 关于运动时间 的函数表达式为 ,其图象如图所示,若小球发射后第2秒与第6秒时的高度相等,则下列时刻中小球的高度最高的是( )
A.第3秒 B.第3.5秒 C.第4秒 D.第6秒
7.(2020·温州模拟)已知抛物线y=x2-2x-m+1(m为常数,m>0)与x轴交于A、B两点(点B在点A的右侧),点P为抛物线在第四象限上的一点,抛物线的对称轴与x轴交于点H,点D在对称轴上,PD=m,取HD的中点C,连结CP、BP,若PH平分∠BPC,BP=2PC,则m的值是( )
A.1 B.2 C.3 D.4
8.为搞好环保,某公司准备修建一个长方体的污水处理池,池底矩形的周长为100m,则池底的最大面积是( )
A.600 m2 B.625 m2 C.650 m2 D.675 m2
9.(2023八下·浦江月考)如图1所示的矩形窗框ABCD的周长及其两条隔断EF、GH的总长为a米,且隔断EF、GH分别与矩形的两条邻边平行,设BC的长为x米,矩形ABCD的面积为y平方米,y关于x的函数图象如图2,则下列说法正确的是( )
A.矩形ABCD的最大面积为8平方米
B.y与x之间的函数关系式为y=-x2+2x
C.当x=4时,矩形ABCD的面积最大
D.a的值为12
10.(2023九上·宜都月考)已知抛物线y=x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为(,3),P是抛物线y=x2+1上一个动点,则△PMF周长的最小值是( )
A.3 B.4 C.5 D.6
二、填空题
11.(2024·上海模拟)某镇的一种特产由于运输原因,长期只能在当地销售.当地政府对该特产的销售投资与收益的关系为:每投入x万元,可获得利润(万元).每年最多可投入100万元的销售投资,则5年所获利润的最大值是 万元.
12.(2024九上·合江月考)如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数与的图象,则阴影部分的面积是 .
13.(2023九上·定远月考)某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线(单位:米)的一部分,则水喷出的最大高度是 米;
14.(2025·虹口模拟)如图,正方形的顶点、在轴上,点、恰好在抛物线上,那么正方形的面积是 .
15.(2020·石家庄模拟)一名男生推铅球,铅球行进高度 (单位: )与水平距离 (单位: )之间的关系是 ,则铅球推出的距离是 .此时铅球行进高度是 .
16.(2020九上·海曙期末)如图抛物线y=-x2-2x+3与x轴交于A,B,与y轴交于点C,点P为顶点,线段PA上有一动点D,以CD为底边向下作等腰三角形△CDE,且∠DEC=90°,则AE的最小值为 。
三、计算题
17.(2024九上·北京市期中)小明进行铅球训练,他尝试利用数学模型来研究铅球的运动情况.他以水平方向为轴方向,为单位长度,建立了如图所示的平面直角坐标系,铅球从轴上的点出手,运动路径可看作抛物线,在点处达到最高位置,落在轴上的点处.小明某次试投时的数据如图所示.
(1)根据图中信息,求出铅球路径所在抛物线的表达式;
(2)若铅球投掷距离(铅球落地点与出手点的水平距离的长度)不小于,成绩为优秀.请通过计算,判断小明此次试投的成绩是否能达到优秀.
18.(2025·温州模拟)2022卡塔尔世界杯足球比赛正在进行阿根廷和荷兰的决赛,阿根廷球员梅西在距球门底部中心点O的正前方处起脚射门,足球沿抛物线向球门中心线;当足球飞离地面高度为时达到最高点,此时足球飞行的水平距离为.已知球门的横梁高为.
(1)建立如图所示直角坐标系,求抛物线解析式;
(2)梅西的射门,足球能否射进球门(不考虑其他影响因素)?
(3)守门员乙站在距离球门处,他跳起时手的最大摸高为,他能阻止球员甲的此次射门吗?
19.(2022九上·武汉月考)如图,一座温室实验室的横截面由抛物线和矩形组成,矩形的长是16m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=-x2+bx+c表示,CD为一排平行于地面的加湿管.
(1)求抛物线的函数关系式,并计算出拱顶到地面的距离.
(2)若加湿管的长度至少是12m,加湿管与拱顶的距离至少是多少米?
(3)若在加湿管上方还要再安装一排恒温管(两排管道互相平行),且恒温管与加湿管相距1.25m,恒温管的长度至少是多少米?
四、解答题
20.(2023九上·湘潭月考)如图,某单位准备将院内一块长米、宽米的长方形空地,建成一个矩形花园,要求在花园中修建两条纵向和一条横向的小道,剩余的地方种植花草.(注:所有小道进出口的宽度相等.)
(1)设小道进出口的宽度为米,种植花草的面积为平方米,则与之间的函数表达式为____________
(2)当种植花草的面积为平方米时,那么小道进出口的宽度为多少米?
21.如图,等腰梯形的周长为60,底角为30°,腰长为x,面积为y,试写出y与x的函数表达式.
22.(2024九下·连云港期中)某公司电商平台,在2021年五一长假期间,举行了商品打折促销活动,经市场调查发现,某种商品的周销售量y(件)是关于售价x(元/件)的一次函数,下表仅列出了该商品的售价x,周销售量y,周销售利润W(元)的三组对应值数据.
x 40 70 90
y 180 90 30
W 3600 4500 2100
(1)求y关于x的函数解析式(不要求写出自变量的取值范围);
(2)若该商品进价a(元/件),售价x为多少时,周销售利润W最大?并求出此时的最大利润;
(3)因疫情期间,该商品进价提高了m(元/件)(),公司为回馈消费者,规定该商品售价x不得超过55(元/件),且该商品在今后的销售中,周销售量与售价仍满足(1)中的函数关系,若周销售最大利润是4050元,求m的值.
23.蔬菜大棚是一种具有出色的保温性能的框架覆膜结构,它出现使得人们可以吃到反季节蔬菜.一般蔬菜大棚使用竹结构或者钢结构的骨架,上面覆上一层或多层保温塑料膜,这样就形成了一个温室空间.如图,某个温室大棚的横截面可以看作矩形和抛物线构成,其中,,取中点O,过点O作线段的垂直平分线交抛物线于点E,若以O点为原点,所在直线为x轴,为y轴建立如图所示平面直角坐标系.
请回答下列问题:
(1)如图,抛物线的顶点,求抛物线的解析式;
(2)如图,为了保证蔬菜大棚的通风性,该大棚要安装两个正方形孔的排气装置,,若,求两个正方形装置的间距的长;
(3)如图,在某一时刻,太阳光线透过A点恰好照射到C点,此时大棚截面的阴影为,求的长.
答案解析部分
1.【答案】D
【知识点】二次函数的实际应用-抛球问题
2.【答案】C
【知识点】列二次函数关系式
3.【答案】C
【知识点】二次函数的实际应用-拱桥问题
4.【答案】B
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-拱桥问题
5.【答案】D
【知识点】二次函数的实际应用-抛球问题
6.【答案】C
【知识点】二次函数的实际应用-抛球问题
7.【答案】A
【知识点】二次函数的实际应用-几何问题
8.【答案】B
【知识点】二次函数的实际应用-几何问题
9.【答案】D
【知识点】二次函数的实际应用-几何问题
10.【答案】C
【知识点】二次函数的实际应用-几何问题
11.【答案】205
【知识点】二次函数的实际应用-销售问题
12.【答案】8
【知识点】二次函数的实际应用-几何问题
13.【答案】2
【知识点】二次函数的实际应用-喷水问题
14.【答案】
【知识点】正方形的性质;二次函数的实际应用-几何问题
15.【答案】;
【知识点】二次函数的实际应用-抛球问题
16.【答案】
【知识点】二次函数的实际应用-几何问题
17.【答案】(1)
(2)能达到优秀
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-抛球问题
18.【答案】(1)解:抛物线的顶点坐标是,
设抛物线的解析式是,
把代入,得,
解得,
则抛物线解析式为:;
(2)解: 当时,,
故:能射进球门;
答:足球能射进球门.
(3)解:当时,,
∴守门员乙不能阻止球员甲的此次射门,
当时,,
解得:(舍去),
∴,
答:他至少后退,才能阻止球员甲的射门.
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-抛球问题
19.【答案】(1)y=-x2+x+4,拱顶到地面的距离为8米
(2)至少是2.25米
(3)至少是8米
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-拱桥问题
20.【答案】(1)
(2)小道进出口的宽度为米
【知识点】一元二次方程的应用-几何问题;二次函数的实际应用-几何问题
21.【答案】解:作AE⊥BC,
在Rt△ABE中,∠B=30°,
则AE= AB= x,
∵四边形ABCD是等腰梯形,
∴AD+BC=60﹣AB﹣CD=60﹣2x,
∴S= (AD+BC)×AE= (60﹣2x)× x=﹣ x2+15x(0<x<60).
【知识点】列二次函数关系式
22.【答案】解:(1)设,由题意有
,解得,
所以y关于x的函数解析式为;
(2)由(1),又由表可得:
,,
.
所以售价时,周销售利润W最大,最大利润为4800;
(3)由题意,
其对称轴,时上述函数单调递增,
所以只有时周销售利润最大,.
.
【知识点】二次函数的实际应用-销售问题;一次函数的实际应用-销售问题
23.【答案】(1)解:根据题意可得:抛物线的顶点,
设抛物线的解析式为,
∵四边形为矩形,为的中垂线,
∴,,
∵,
∴点,代入,
得:,
∴,
∴抛物线的解析式为;
(2)解:∵四边形,四边形均为正方形,,
∴,
延长交于点,延长交于点,则四边形,四边形均为矩形,如图所示:
∴,
∴,
∵,当时,,解得:,
∴,,
∴,
∴;
(3)解:∵,垂直平分,
∴,
∴,
设直线的解析式为,
则:,解得:,
∴,
∵太阳光为平行光,
设过点平行于的光线的解析式为,
由题意,得:与抛物线相切,
联立,整理得:,
则:,解得:;
∴,当时,,
∴,
∵,
∴.
【知识点】一元二次方程根的判别式及应用;矩形的判定与性质;二次函数的实际应用-几何问题
21世纪教育网(www.21cnjy.com)
2 / 13
22.3 实际问题与二次函数
一、单选题
1.(2025九下·河西开学考)一名男生推铅球,铅球出手时,铅球的高度为.铅球行进的高度(单位:)是水平距离(单位:)的二次函数,与之间的函数关系式为.有下列结论:
①从铅球出手到落地时水平距离为;
②铅球行进过程中的高度可以达到;
③铅球从出手到飞行至最高点的水平距离小于从最高点运动至落地的水平距离.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
2.(2023九上·集美期中)据省统计局公布的数据,合肥市2023年第一季度总值约为2.6千亿元人民币,若我市第三季度总值为y千亿元人民币,平均每个季度GDP增长的百分率为x,则y关于x的函数表达式是( )
A. B.
C. D.
3.(2023九上·徐州期中)图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面,水面宽,如图(2)建立平面直角坐标系,则抛物线的关系式是( )
A. B. C. D.
4.(2023九下·天山模拟)某池塘的截面如图所示,池底呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:m).有下列结论:
①;
②池底所在抛物线的解析式为;
③池塘最深处到水面CD的距离为1.8m;
④若池塘中水面的宽度减少为原来的一半,
则最深处到水面的距离减少为原来的.
其中结论正确的是( )
A.①② B.②④ C.③④ D.①④
5.(2024九上·金湾期中)如图,小强在某次投篮中,球的运动路线是抛物线的一部分,若命中篮圈中心,则他与篮筐底的距离是( )
A. B. C. D.
6.(2021九上·余杭期末)竖直向上发射的小球的高度 关于运动时间 的函数表达式为 ,其图象如图所示,若小球发射后第2秒与第6秒时的高度相等,则下列时刻中小球的高度最高的是( )
A.第3秒 B.第3.5秒 C.第4秒 D.第6秒
7.(2020·温州模拟)已知抛物线y=x2-2x-m+1(m为常数,m>0)与x轴交于A、B两点(点B在点A的右侧),点P为抛物线在第四象限上的一点,抛物线的对称轴与x轴交于点H,点D在对称轴上,PD=m,取HD的中点C,连结CP、BP,若PH平分∠BPC,BP=2PC,则m的值是( )
A.1 B.2 C.3 D.4
8.为搞好环保,某公司准备修建一个长方体的污水处理池,池底矩形的周长为100m,则池底的最大面积是( )
A.600 m2 B.625 m2 C.650 m2 D.675 m2
9.(2023八下·浦江月考)如图1所示的矩形窗框ABCD的周长及其两条隔断EF、GH的总长为a米,且隔断EF、GH分别与矩形的两条邻边平行,设BC的长为x米,矩形ABCD的面积为y平方米,y关于x的函数图象如图2,则下列说法正确的是( )
A.矩形ABCD的最大面积为8平方米
B.y与x之间的函数关系式为y=-x2+2x
C.当x=4时,矩形ABCD的面积最大
D.a的值为12
10.(2023九上·宜都月考)已知抛物线y=x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为(,3),P是抛物线y=x2+1上一个动点,则△PMF周长的最小值是( )
A.3 B.4 C.5 D.6
二、填空题
11.(2024·上海模拟)某镇的一种特产由于运输原因,长期只能在当地销售.当地政府对该特产的销售投资与收益的关系为:每投入x万元,可获得利润(万元).每年最多可投入100万元的销售投资,则5年所获利润的最大值是 万元.
12.(2024九上·合江月考)如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数与的图象,则阴影部分的面积是 .
13.(2023九上·定远月考)某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线(单位:米)的一部分,则水喷出的最大高度是 米;
14.(2025·虹口模拟)如图,正方形的顶点、在轴上,点、恰好在抛物线上,那么正方形的面积是 .
15.(2020·石家庄模拟)一名男生推铅球,铅球行进高度 (单位: )与水平距离 (单位: )之间的关系是 ,则铅球推出的距离是 .此时铅球行进高度是 .
16.(2020九上·海曙期末)如图抛物线y=-x2-2x+3与x轴交于A,B,与y轴交于点C,点P为顶点,线段PA上有一动点D,以CD为底边向下作等腰三角形△CDE,且∠DEC=90°,则AE的最小值为 。
三、计算题
17.(2024九上·北京市期中)小明进行铅球训练,他尝试利用数学模型来研究铅球的运动情况.他以水平方向为轴方向,为单位长度,建立了如图所示的平面直角坐标系,铅球从轴上的点出手,运动路径可看作抛物线,在点处达到最高位置,落在轴上的点处.小明某次试投时的数据如图所示.
(1)根据图中信息,求出铅球路径所在抛物线的表达式;
(2)若铅球投掷距离(铅球落地点与出手点的水平距离的长度)不小于,成绩为优秀.请通过计算,判断小明此次试投的成绩是否能达到优秀.
18.(2025·温州模拟)2022卡塔尔世界杯足球比赛正在进行阿根廷和荷兰的决赛,阿根廷球员梅西在距球门底部中心点O的正前方处起脚射门,足球沿抛物线向球门中心线;当足球飞离地面高度为时达到最高点,此时足球飞行的水平距离为.已知球门的横梁高为.
(1)建立如图所示直角坐标系,求抛物线解析式;
(2)梅西的射门,足球能否射进球门(不考虑其他影响因素)?
(3)守门员乙站在距离球门处,他跳起时手的最大摸高为,他能阻止球员甲的此次射门吗?
19.(2022九上·武汉月考)如图,一座温室实验室的横截面由抛物线和矩形组成,矩形的长是16m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=-x2+bx+c表示,CD为一排平行于地面的加湿管.
(1)求抛物线的函数关系式,并计算出拱顶到地面的距离.
(2)若加湿管的长度至少是12m,加湿管与拱顶的距离至少是多少米?
(3)若在加湿管上方还要再安装一排恒温管(两排管道互相平行),且恒温管与加湿管相距1.25m,恒温管的长度至少是多少米?
四、解答题
20.(2023九上·湘潭月考)如图,某单位准备将院内一块长米、宽米的长方形空地,建成一个矩形花园,要求在花园中修建两条纵向和一条横向的小道,剩余的地方种植花草.(注:所有小道进出口的宽度相等.)
(1)设小道进出口的宽度为米,种植花草的面积为平方米,则与之间的函数表达式为____________
(2)当种植花草的面积为平方米时,那么小道进出口的宽度为多少米?
21.如图,等腰梯形的周长为60,底角为30°,腰长为x,面积为y,试写出y与x的函数表达式.
22.(2024九下·连云港期中)某公司电商平台,在2021年五一长假期间,举行了商品打折促销活动,经市场调查发现,某种商品的周销售量y(件)是关于售价x(元/件)的一次函数,下表仅列出了该商品的售价x,周销售量y,周销售利润W(元)的三组对应值数据.
x 40 70 90
y 180 90 30
W 3600 4500 2100
(1)求y关于x的函数解析式(不要求写出自变量的取值范围);
(2)若该商品进价a(元/件),售价x为多少时,周销售利润W最大?并求出此时的最大利润;
(3)因疫情期间,该商品进价提高了m(元/件)(),公司为回馈消费者,规定该商品售价x不得超过55(元/件),且该商品在今后的销售中,周销售量与售价仍满足(1)中的函数关系,若周销售最大利润是4050元,求m的值.
23.蔬菜大棚是一种具有出色的保温性能的框架覆膜结构,它出现使得人们可以吃到反季节蔬菜.一般蔬菜大棚使用竹结构或者钢结构的骨架,上面覆上一层或多层保温塑料膜,这样就形成了一个温室空间.如图,某个温室大棚的横截面可以看作矩形和抛物线构成,其中,,取中点O,过点O作线段的垂直平分线交抛物线于点E,若以O点为原点,所在直线为x轴,为y轴建立如图所示平面直角坐标系.
请回答下列问题:
(1)如图,抛物线的顶点,求抛物线的解析式;
(2)如图,为了保证蔬菜大棚的通风性,该大棚要安装两个正方形孔的排气装置,,若,求两个正方形装置的间距的长;
(3)如图,在某一时刻,太阳光线透过A点恰好照射到C点,此时大棚截面的阴影为,求的长.
答案解析部分
1.【答案】D
【知识点】二次函数的实际应用-抛球问题
2.【答案】C
【知识点】列二次函数关系式
3.【答案】C
【知识点】二次函数的实际应用-拱桥问题
4.【答案】B
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-拱桥问题
5.【答案】D
【知识点】二次函数的实际应用-抛球问题
6.【答案】C
【知识点】二次函数的实际应用-抛球问题
7.【答案】A
【知识点】二次函数的实际应用-几何问题
8.【答案】B
【知识点】二次函数的实际应用-几何问题
9.【答案】D
【知识点】二次函数的实际应用-几何问题
10.【答案】C
【知识点】二次函数的实际应用-几何问题
11.【答案】205
【知识点】二次函数的实际应用-销售问题
12.【答案】8
【知识点】二次函数的实际应用-几何问题
13.【答案】2
【知识点】二次函数的实际应用-喷水问题
14.【答案】
【知识点】正方形的性质;二次函数的实际应用-几何问题
15.【答案】;
【知识点】二次函数的实际应用-抛球问题
16.【答案】
【知识点】二次函数的实际应用-几何问题
17.【答案】(1)
(2)能达到优秀
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-抛球问题
18.【答案】(1)解:抛物线的顶点坐标是,
设抛物线的解析式是,
把代入,得,
解得,
则抛物线解析式为:;
(2)解: 当时,,
故:能射进球门;
答:足球能射进球门.
(3)解:当时,,
∴守门员乙不能阻止球员甲的此次射门,
当时,,
解得:(舍去),
∴,
答:他至少后退,才能阻止球员甲的射门.
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-抛球问题
19.【答案】(1)y=-x2+x+4,拱顶到地面的距离为8米
(2)至少是2.25米
(3)至少是8米
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-拱桥问题
20.【答案】(1)
(2)小道进出口的宽度为米
【知识点】一元二次方程的应用-几何问题;二次函数的实际应用-几何问题
21.【答案】解:作AE⊥BC,
在Rt△ABE中,∠B=30°,
则AE= AB= x,
∵四边形ABCD是等腰梯形,
∴AD+BC=60﹣AB﹣CD=60﹣2x,
∴S= (AD+BC)×AE= (60﹣2x)× x=﹣ x2+15x(0<x<60).
【知识点】列二次函数关系式
22.【答案】解:(1)设,由题意有
,解得,
所以y关于x的函数解析式为;
(2)由(1),又由表可得:
,,
.
所以售价时,周销售利润W最大,最大利润为4800;
(3)由题意,
其对称轴,时上述函数单调递增,
所以只有时周销售利润最大,.
.
【知识点】二次函数的实际应用-销售问题;一次函数的实际应用-销售问题
23.【答案】(1)解:根据题意可得:抛物线的顶点,
设抛物线的解析式为,
∵四边形为矩形,为的中垂线,
∴,,
∵,
∴点,代入,
得:,
∴,
∴抛物线的解析式为;
(2)解:∵四边形,四边形均为正方形,,
∴,
延长交于点,延长交于点,则四边形,四边形均为矩形,如图所示:
∴,
∴,
∵,当时,,解得:,
∴,,
∴,
∴;
(3)解:∵,垂直平分,
∴,
∴,
设直线的解析式为,
则:,解得:,
∴,
∵太阳光为平行光,
设过点平行于的光线的解析式为,
由题意,得:与抛物线相切,
联立,整理得:,
则:,解得:;
∴,当时,,
∴,
∵,
∴.
【知识点】一元二次方程根的判别式及应用;矩形的判定与性质;二次函数的实际应用-几何问题
21世纪教育网(www.21cnjy.com)
2 / 13
同课章节目录
