第22章 二次函数 同步练习(含答案)
文档属性
| 名称 | 第22章 二次函数 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 463.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 21:29:14 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第22章二次函数
一、单选题
1.(2023九上·番禺期中)二次函数的图象经过,则的值为( )
A. B. C.1 D.2
2.(2022九上·双滦期中)抛物线y=x2-x-6与x轴的交点坐标是( )
A.(3,0) B.(-2,0)
C.(-6,0),(1,0) D.(3,0),(-2,0)
3.(2024九上·濠江月考)将抛物线向左平移2个单位长度,所得新抛物线的函数解析式为( )
A. B. C. D.
4.(2017九上·临沭期末)已知二次函数 有最大值1,则该函数图象的顶点坐标为( )
A.(-3,-1) B.(-3,1) C.(3,1) D.(3,-1)
5.(2023九上·万宁期中)如图为,则( )
A.,, B.,,
C.,, D.,,
6.(2024九下·杭州月考)设二次函数(,m,k是实数),则( )
A.当时,函数y的最大值为 B.当时,函数y的最大值为
C.当时,函数y的最大值为 D.当时,函数y的最大值为
7.(2020九上·包河期末)如图,抛物线y=ax2+bx+c经过(-1,0)和(0,-1)两点,则抛物线y=cx2+bx+a的图象大致为( )
A. B.
C. D.
8.(2024·滨江模拟)二次函数.为常数,且中的与的部分对应值如下表:
-1 0 1 3
-1 3 5 3
下列结论:①该函数图象的开口向下;
②该函数图象的顶点坐标为;
③当时,随的增大而减少;
④是方程的一个根.
确的是( )
A.①② B.②③ C.③④ D.①④
9.设b>0,二次函数y=ax2+bx+a2﹣1的图象为下列之一,则a的值为( )
A.1 B.﹣1 C. D.
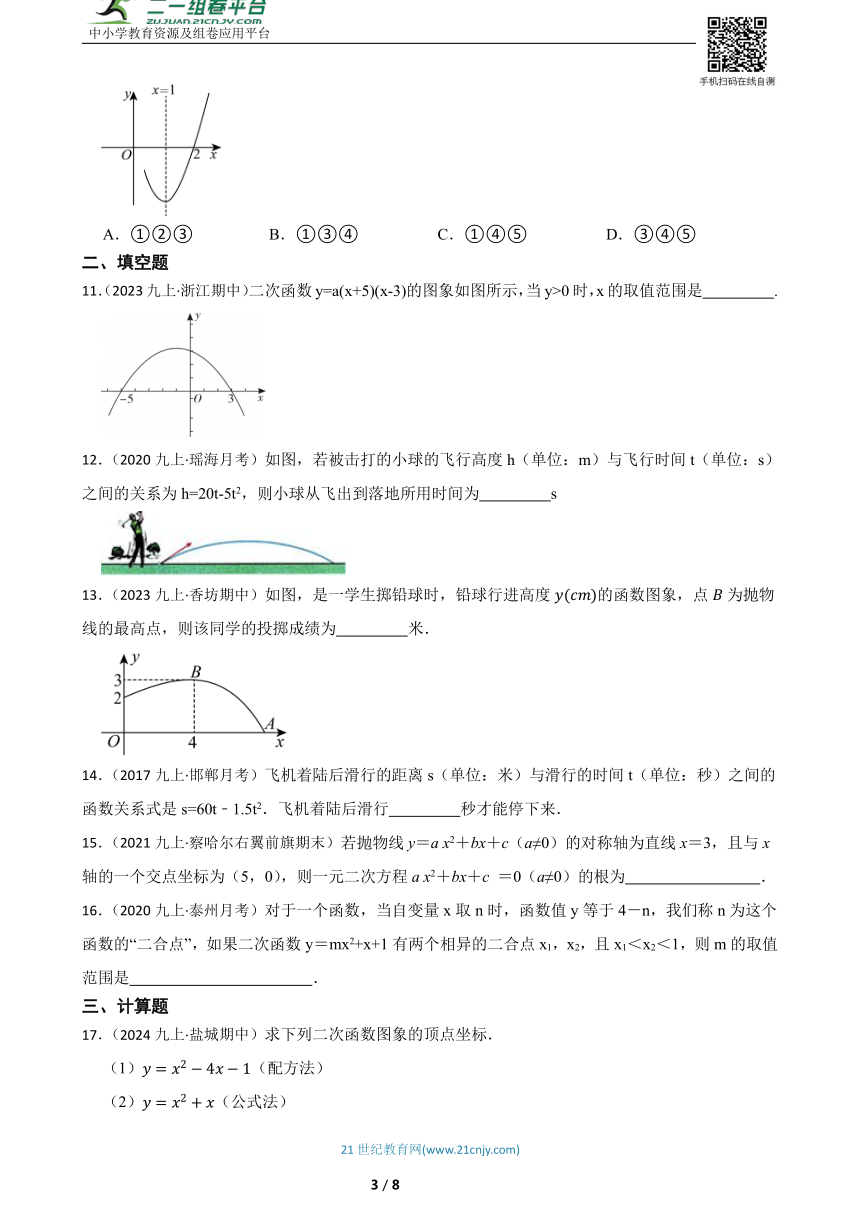
10.(2024九上·许昌月考)抛物线y=ax2+bx+c(a≠0)与x轴的一个交点坐标为(2,0),对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:其中正确的是( )
①抛物线过原点:
②a﹣b+c<0:
③2a+b+c=0;
④抛物线顶点为(1,):
⑤当x<1时,y随x的增大而增大
A.①②③ B.①③④ C.①④⑤ D.③④⑤
二、填空题
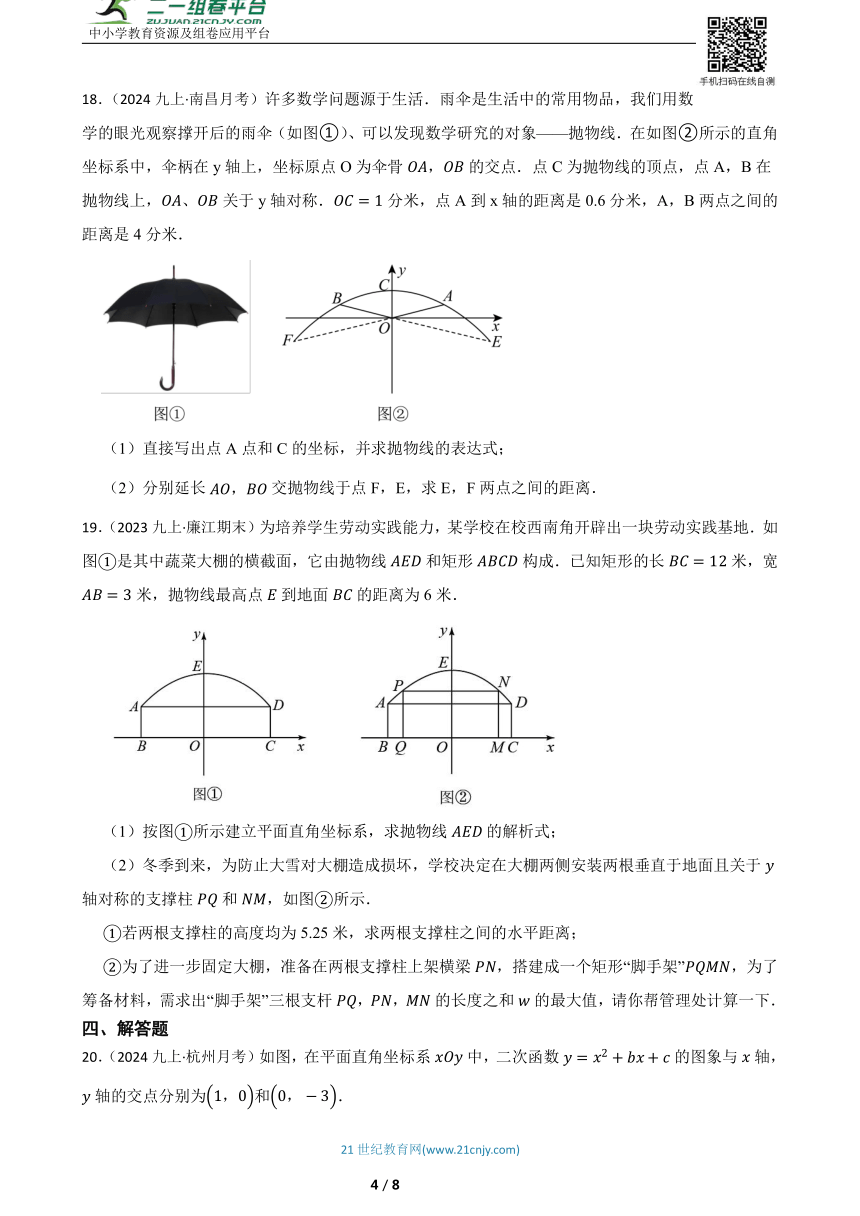
11.(2023九上·浙江期中)二次函数y=a(x+5)(x-3)的图象如图所示,当y>0时,x的取值范围是 .
12.(2020九上·瑶海月考)如图,若被击打的小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的关系为h=20t-5t2,则小球从飞出到落地所用时间为 s
13.(2023九上·香坊期中)如图,是一学生掷铅球时,铅球行进高度的函数图象,点为抛物线的最高点,则该同学的投掷成绩为 米.
14.(2017九上·邯郸月考)飞机着陆后滑行的距离s(单位:米)与滑行的时间t(单位:秒)之间的函数关系式是s=60t﹣1.5t2.飞机着陆后滑行 秒才能停下来.
15.(2021九上·察哈尔右翼前旗期末)若抛物线y=a x2+bx+c(a≠0)的对称轴为直线x=3,且与x轴的一个交点坐标为(5,0),则一元二次方程a x2+bx+c =0(a≠0)的根为 .
16.(2020九上·泰州月考)对于一个函数,当自变量x取n时,函数值y等于4-n,我们称n为这个函数的“二合点”,如果二次函数y=mx2+x+1有两个相异的二合点x1,x2,且x1<x2<1,则m的取值范围是 .
三、计算题
17.(2024九上·盐城期中)求下列二次函数图象的顶点坐标.
(1)(配方法)
(2)(公式法)
18.(2024九上·南昌月考)许多数学问题源于生活.雨伞是生活中的常用物品,我们用数学的眼光观察撑开后的雨伞(如图①)、可以发现数学研究的对象——抛物线.在如图②所示的直角坐标系中,伞柄在y轴上,坐标原点O为伞骨,的交点.点C为抛物线的顶点,点A,B在抛物线上,、关于y轴对称.分米,点A到x轴的距离是0.6分米,A,B两点之间的距离是4分米.
(1)直接写出点A点和C的坐标,并求抛物线的表达式;
(2)分别延长交抛物线于点F,E,求E,F两点之间的距离.
19.(2023九上·廉江期末)为培养学生劳动实践能力,某学校在校西南角开辟出一块劳动实践基地.如图是其中蔬菜大棚的横截面,它由抛物线和矩形构成.已知矩形的长米,宽米,抛物线最高点到地面的距离为6米.
(1)按图所示建立平面直角坐标系,求抛物线的解析式;
(2)冬季到来,为防止大雪对大棚造成损坏,学校决定在大棚两侧安装两根垂直于地面且关于轴对称的支撑柱和,如图所示.
若两根支撑柱的高度均为5.25米,求两根支撑柱之间的水平距离;
为了进一步固定大棚,准备在两根支撑柱上架横梁,搭建成一个矩形“脚手架”,为了筹备材料,需求出“脚手架”三根支杆,,的长度之和的最大值,请你帮管理处计算一下.
四、解答题
20.(2024九上·杭州月考)如图,在平面直角坐标系中,二次函数的图象与轴,轴的交点分别为和.
(1)求此二次函数的表达式;并写出其对称轴与顶点坐标;
(2)结合函数图象,直接写出当时,的取值范围.
21.(2024九上·余杭月考)已知二次函数.求该二次函数图象的顶点坐标和对称轴.
22.(2023九上·诸暨月考)某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)如果设涨价为元,销量为_______.(请用含的代数式表示)
(2)该玩具销售单价定为多少元时,商场能获得12000元的销售利润?
(3)若玩具厂规定该品牌玩具销售单价不低于46元,且商场要完成不少于500件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
23.(2023九上·广州月考)如图,已知抛物线与轴交于点和,与轴交于.
(1)求抛物线的解析式,并求出顶点的坐标.
(2)观察图象,直接写出一元二次不等式:解集为:
(3)若抛物线的对称轴交轴于点,求四边形的面积.
答案解析部分
1.【答案】D
【知识点】待定系数法求二次函数解析式
2.【答案】D
【知识点】二次函数图象与坐标轴的交点问题
3.【答案】B
【知识点】二次函数图象的几何变换
4.【答案】B
【知识点】二次函数的最值;二次函数y=a(x-h)²+k的性质
5.【答案】A
【知识点】二次函数图象与系数的关系
6.【答案】D
【知识点】二次函数的最值
7.【答案】B
【知识点】二次函数y=ax²+bx+c的图象;二次函数y=ax²+bx+c的性质
8.【答案】D
【知识点】二次函数y=ax²+bx+c的图象;二次函数y=ax²+bx+c的性质;二次函数与一元二次方程的综合应用
9.【答案】B
【知识点】二次函数图象与系数的关系
10.【答案】B
【知识点】二次函数图象与系数的关系
11.【答案】-5【知识点】二次函数图象与坐标轴的交点问题;二次函数与不等式(组)的综合应用
12.【答案】4
【知识点】二次函数的实际应用-抛球问题
13.【答案】
【知识点】二次函数的实际应用-抛球问题
14.【答案】20
【知识点】二次函数y=a(x-h)²+k的性质;二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
15.【答案】xl=5,x2=1
【知识点】二次函数与一元二次方程的综合应用
16.【答案】﹣ <m<0或m>1
【知识点】一元二次方程根的判别式及应用;二次函数图象与系数的关系
17.【答案】(1)
(2)
【知识点】二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
18.【答案】(1)点A的坐标为、点C的坐标为,
(2)10
【知识点】待定系数法求二次函数解析式
19.【答案】(1)
(2)两根支撑柱之间的水平距离为6米“脚手架”三根支杆,,的长度之和的最大值为18米
【知识点】二次函数的最值;待定系数法求二次函数解析式;二次函数的实际应用-几何问题
20.【答案】(1)表达式为,对称轴为直线,顶点坐标为
(2)或
【知识点】待定系数法求二次函数解析式
21.【答案】顶点坐标为,对称轴为直线
【知识点】二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
22.【答案】(1)件;(2)60元或70元;(3)10000元.
【知识点】二次函数的实际应用-销售问题
23.【答案】(1)解:抛物线与轴交于,
,
,
把、代入中,得
,
解得,
二次函数的解析式是,也即,
其顶点的坐标是;
(2)或
(3)解:.
【知识点】待定系数法求二次函数解析式;二次函数与不等式(组)的综合应用;二次函数y=ax²+bx+c的性质
21世纪教育网(www.21cnjy.com)
2 / 9
第22章二次函数
一、单选题
1.(2023九上·番禺期中)二次函数的图象经过,则的值为( )
A. B. C.1 D.2
2.(2022九上·双滦期中)抛物线y=x2-x-6与x轴的交点坐标是( )
A.(3,0) B.(-2,0)
C.(-6,0),(1,0) D.(3,0),(-2,0)
3.(2024九上·濠江月考)将抛物线向左平移2个单位长度,所得新抛物线的函数解析式为( )
A. B. C. D.
4.(2017九上·临沭期末)已知二次函数 有最大值1,则该函数图象的顶点坐标为( )
A.(-3,-1) B.(-3,1) C.(3,1) D.(3,-1)
5.(2023九上·万宁期中)如图为,则( )
A.,, B.,,
C.,, D.,,
6.(2024九下·杭州月考)设二次函数(,m,k是实数),则( )
A.当时,函数y的最大值为 B.当时,函数y的最大值为
C.当时,函数y的最大值为 D.当时,函数y的最大值为
7.(2020九上·包河期末)如图,抛物线y=ax2+bx+c经过(-1,0)和(0,-1)两点,则抛物线y=cx2+bx+a的图象大致为( )
A. B.
C. D.
8.(2024·滨江模拟)二次函数.为常数,且中的与的部分对应值如下表:
-1 0 1 3
-1 3 5 3
下列结论:①该函数图象的开口向下;
②该函数图象的顶点坐标为;
③当时,随的增大而减少;
④是方程的一个根.
确的是( )
A.①② B.②③ C.③④ D.①④
9.设b>0,二次函数y=ax2+bx+a2﹣1的图象为下列之一,则a的值为( )
A.1 B.﹣1 C. D.
10.(2024九上·许昌月考)抛物线y=ax2+bx+c(a≠0)与x轴的一个交点坐标为(2,0),对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:其中正确的是( )
①抛物线过原点:
②a﹣b+c<0:
③2a+b+c=0;
④抛物线顶点为(1,):
⑤当x<1时,y随x的增大而增大
A.①②③ B.①③④ C.①④⑤ D.③④⑤
二、填空题
11.(2023九上·浙江期中)二次函数y=a(x+5)(x-3)的图象如图所示,当y>0时,x的取值范围是 .
12.(2020九上·瑶海月考)如图,若被击打的小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的关系为h=20t-5t2,则小球从飞出到落地所用时间为 s
13.(2023九上·香坊期中)如图,是一学生掷铅球时,铅球行进高度的函数图象,点为抛物线的最高点,则该同学的投掷成绩为 米.
14.(2017九上·邯郸月考)飞机着陆后滑行的距离s(单位:米)与滑行的时间t(单位:秒)之间的函数关系式是s=60t﹣1.5t2.飞机着陆后滑行 秒才能停下来.
15.(2021九上·察哈尔右翼前旗期末)若抛物线y=a x2+bx+c(a≠0)的对称轴为直线x=3,且与x轴的一个交点坐标为(5,0),则一元二次方程a x2+bx+c =0(a≠0)的根为 .
16.(2020九上·泰州月考)对于一个函数,当自变量x取n时,函数值y等于4-n,我们称n为这个函数的“二合点”,如果二次函数y=mx2+x+1有两个相异的二合点x1,x2,且x1<x2<1,则m的取值范围是 .
三、计算题
17.(2024九上·盐城期中)求下列二次函数图象的顶点坐标.
(1)(配方法)
(2)(公式法)
18.(2024九上·南昌月考)许多数学问题源于生活.雨伞是生活中的常用物品,我们用数学的眼光观察撑开后的雨伞(如图①)、可以发现数学研究的对象——抛物线.在如图②所示的直角坐标系中,伞柄在y轴上,坐标原点O为伞骨,的交点.点C为抛物线的顶点,点A,B在抛物线上,、关于y轴对称.分米,点A到x轴的距离是0.6分米,A,B两点之间的距离是4分米.
(1)直接写出点A点和C的坐标,并求抛物线的表达式;
(2)分别延长交抛物线于点F,E,求E,F两点之间的距离.
19.(2023九上·廉江期末)为培养学生劳动实践能力,某学校在校西南角开辟出一块劳动实践基地.如图是其中蔬菜大棚的横截面,它由抛物线和矩形构成.已知矩形的长米,宽米,抛物线最高点到地面的距离为6米.
(1)按图所示建立平面直角坐标系,求抛物线的解析式;
(2)冬季到来,为防止大雪对大棚造成损坏,学校决定在大棚两侧安装两根垂直于地面且关于轴对称的支撑柱和,如图所示.
若两根支撑柱的高度均为5.25米,求两根支撑柱之间的水平距离;
为了进一步固定大棚,准备在两根支撑柱上架横梁,搭建成一个矩形“脚手架”,为了筹备材料,需求出“脚手架”三根支杆,,的长度之和的最大值,请你帮管理处计算一下.
四、解答题
20.(2024九上·杭州月考)如图,在平面直角坐标系中,二次函数的图象与轴,轴的交点分别为和.
(1)求此二次函数的表达式;并写出其对称轴与顶点坐标;
(2)结合函数图象,直接写出当时,的取值范围.
21.(2024九上·余杭月考)已知二次函数.求该二次函数图象的顶点坐标和对称轴.
22.(2023九上·诸暨月考)某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)如果设涨价为元,销量为_______.(请用含的代数式表示)
(2)该玩具销售单价定为多少元时,商场能获得12000元的销售利润?
(3)若玩具厂规定该品牌玩具销售单价不低于46元,且商场要完成不少于500件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
23.(2023九上·广州月考)如图,已知抛物线与轴交于点和,与轴交于.
(1)求抛物线的解析式,并求出顶点的坐标.
(2)观察图象,直接写出一元二次不等式:解集为:
(3)若抛物线的对称轴交轴于点,求四边形的面积.
答案解析部分
1.【答案】D
【知识点】待定系数法求二次函数解析式
2.【答案】D
【知识点】二次函数图象与坐标轴的交点问题
3.【答案】B
【知识点】二次函数图象的几何变换
4.【答案】B
【知识点】二次函数的最值;二次函数y=a(x-h)²+k的性质
5.【答案】A
【知识点】二次函数图象与系数的关系
6.【答案】D
【知识点】二次函数的最值
7.【答案】B
【知识点】二次函数y=ax²+bx+c的图象;二次函数y=ax²+bx+c的性质
8.【答案】D
【知识点】二次函数y=ax²+bx+c的图象;二次函数y=ax²+bx+c的性质;二次函数与一元二次方程的综合应用
9.【答案】B
【知识点】二次函数图象与系数的关系
10.【答案】B
【知识点】二次函数图象与系数的关系
11.【答案】-5
12.【答案】4
【知识点】二次函数的实际应用-抛球问题
13.【答案】
【知识点】二次函数的实际应用-抛球问题
14.【答案】20
【知识点】二次函数y=a(x-h)²+k的性质;二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
15.【答案】xl=5,x2=1
【知识点】二次函数与一元二次方程的综合应用
16.【答案】﹣ <m<0或m>1
【知识点】一元二次方程根的判别式及应用;二次函数图象与系数的关系
17.【答案】(1)
(2)
【知识点】二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
18.【答案】(1)点A的坐标为、点C的坐标为,
(2)10
【知识点】待定系数法求二次函数解析式
19.【答案】(1)
(2)两根支撑柱之间的水平距离为6米“脚手架”三根支杆,,的长度之和的最大值为18米
【知识点】二次函数的最值;待定系数法求二次函数解析式;二次函数的实际应用-几何问题
20.【答案】(1)表达式为,对称轴为直线,顶点坐标为
(2)或
【知识点】待定系数法求二次函数解析式
21.【答案】顶点坐标为,对称轴为直线
【知识点】二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
22.【答案】(1)件;(2)60元或70元;(3)10000元.
【知识点】二次函数的实际应用-销售问题
23.【答案】(1)解:抛物线与轴交于,
,
,
把、代入中,得
,
解得,
二次函数的解析式是,也即,
其顶点的坐标是;
(2)或
(3)解:.
【知识点】待定系数法求二次函数解析式;二次函数与不等式(组)的综合应用;二次函数y=ax²+bx+c的性质
21世纪教育网(www.21cnjy.com)
2 / 9
同课章节目录
