23.1图形的旋转 同步练习(含答案)
文档属性
| 名称 | 23.1图形的旋转 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 405.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 21:28:41 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
23.1图形的旋转
一、单选题
1.(2022八下·贵阳期末)如图,在中,,,,将绕点顺时针旋转得到,点的对应点落在边上,连接,则的周长为( )
A. B. C. D.
2.(2025八下·连云港月考)如图,中,,.将绕点B逆时针旋转得到,使点C的对应点恰好落在边上,则的度数是( )
A. B. C. D.
3.(2021八下·北票期中)如图,在中,,将在平面内绕点逆时针旋转到的位置,且,则旋转角的度数为( )
A. B. C. D.
4.将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,得到数字“6”,现将数字“69”旋转180°,得到的数字是( )
A.96 B.69 C.66 D.99
5.(2024八上·上思月考)通过下列变换能得到全等图形的是( ).
A.只有平移 B.只有平移、旋转
C.只有平移、翻转 D.平移、旋转、翻转
6.(2024九上·蓬江期中)如图,菱形的对角线交于原点O,,.将菱形绕原点O逆时针旋转,每次旋转,则第2023次旋转结束时,点C的坐标为( )
A. B. C. D.
7.如图,该图形绕点O按下列角度旋转后,不能与其自身重合的是( )
A.72° B.108° C.144° D.216°
8.(2016·南山模拟)如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,此时点C恰好在线段DE上,若∠B=40°,∠CAE=60°,则∠DAC的度数为( )
A.15° B.20° C.25° D.30°
9.(2025七上·宜州期末)如图,沿图中虚线旋转一周,能围成的几何体是下面几何体中的( )
A. B. C. D.
10.(2023九上·临海月考)如图,平行四边形中,,,,是边上一点,且,是边上的一个动点,将线段绕点逆时针旋转,得到,连接、,则的最小值是( )
A.4 B. C. D.
二、填空题
11.(2024七上·高碑店月考)如图,一旋转门内部由三块玻璃隔板组成.将此旋转门旋转一周,能形成的几何体是 .
12.(2023八下·沿河月考)如图,把正方形铁片置于平面直角坐标系中,顶点A的坐标为,点在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转,第一次旋转至图①位置,第二次旋转至图②位置,…,则正方形铁片连续旋转2023次后,点P的坐标为 .
13.(2016·江西)如图所示,△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为 .
14.(2016九上·乌拉特前旗期中)钟表的时针匀速旋转一周需要12小时,经过2小时,时针旋转了 度.
15.(2024八上·上海市月考)在等边中,,点O在上,且,点P是上一动点,连接,将线段绕点O逆时针旋转得到线段.要使点D恰好落在边上,则的长是 .
16.(2024九上·信丰期末)如图,一副三角板的三个内角分别是90°,45°,45°和90°,60°,30°,按如图所示叠放在一起(点A,D,B在同一直线上),若固定△ABC,将△BDE绕着公共顶点B顺时针旋转α度(0<α<180),当边DE与△ABC的某一边平行时,相应的旋转角α的值为 .
三、计算题
17.(2023八上·沙坪坝期末)如图1,在平面直角坐标系中,直线:分别与x轴,y轴交于A,B两点,点C为x轴正半轴上一点,且,直线过点C且与y轴交于点D,与直线l1交于第二象限内的点E,已知点E到x轴的距离为.
(1)求点D的坐标;
(2)如图2,在直线上存在一点M,使,求出点M的坐标;
(3)如图3,将绕点O逆时针旋转得到,点P为直线上一动点,点Q为x轴上一动点,连接,,,当为以为腰的等腰直角三角形时,直接写出点P的坐标.
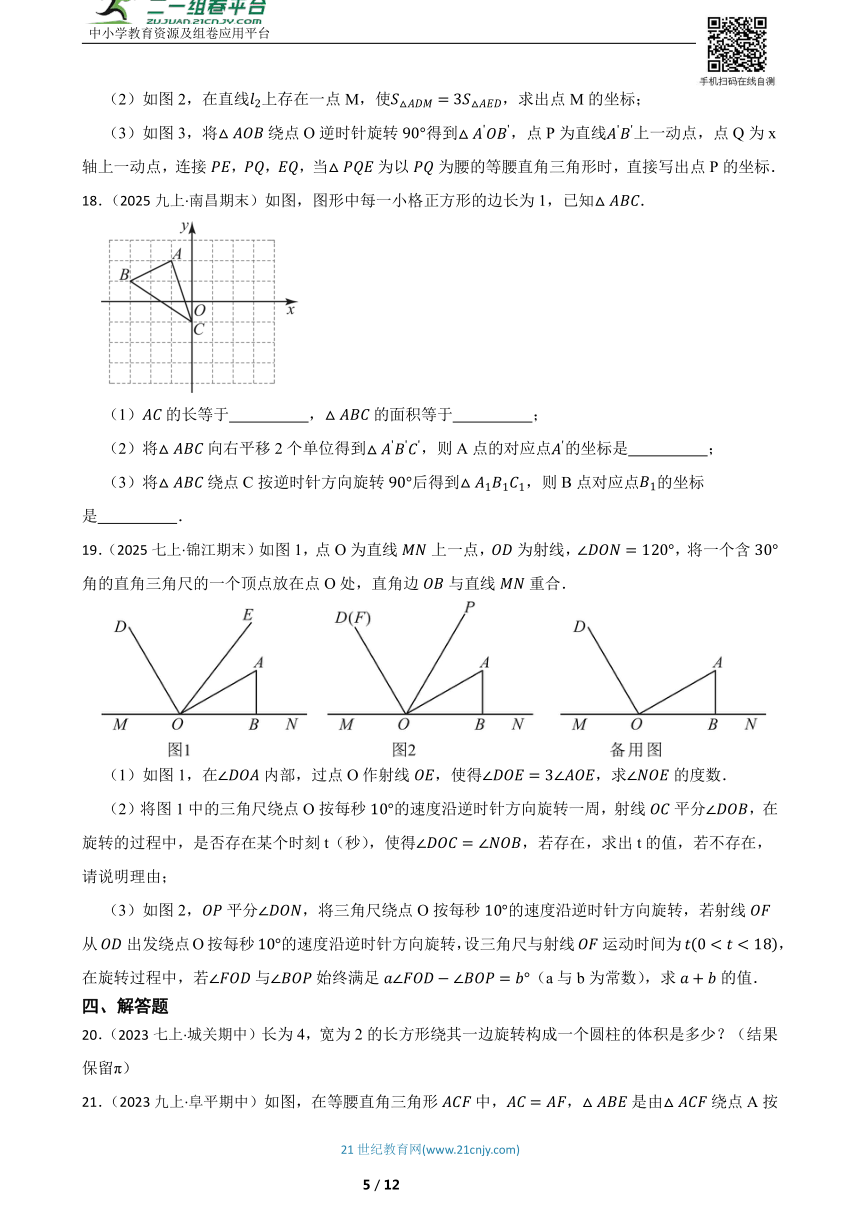
18.(2025九上·南昌期末)如图,图形中每一小格正方形的边长为1,已知.
(1)的长等于 ,的面积等于 ;
(2)将向右平移2个单位得到,则A点的对应点的坐标是 ;
(3)将绕点C按逆时针方向旋转后得到,则B点对应点的坐标是 .
19.(2025七上·锦江期末)如图1,点O为直线上一点,为射线,,将一个含角的直角三角尺的一个顶点放在点O处,直角边与直线重合.
(1)如图1,在内部,过点O作射线,使得,求的度数.
(2)将图1中的三角尺绕点O按每秒的速度沿逆时针方向旋转一周,射线平分,在旋转的过程中,是否存在某个时刻t(秒),使得,若存在,求出t的值,若不存在,请说明理由;
(3)如图2,平分,将三角尺绕点O按每秒的速度沿逆时针方向旋转,若射线从出发绕点O按每秒的速度沿逆时针方向旋转,设三角尺与射线运动时间为,在旋转过程中,若与始终满足(a与b为常数),求的值.
四、解答题
20.(2023七上·城关期中)长为4,宽为2的长方形绕其一边旋转构成一个圆柱的体积是多少?(结果保留π)
21.(2023九上·阜平期中)如图,在等腰直角三角形中,,是由绕点A按顺时针方向旋转得到的,连接.
(1)若,求旋转角的度数和的度数;
(2)判断与之间的数量关系,并说明理由.
22.(2017·农安模拟)问题原型:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.过点D作△BCD的BC边上的高DE,
易证△ABC≌△BDE,从而得到△BCD的面积为 .
初步探究:如图②,在Rt△ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.用含a的代数式表示△BCD的面积,并说明理由.
简单应用:如图③,在等腰三角形ABC中,AB=AC,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.直接写出△BCD的面积.(用含a的代数式表示)
23.(2023九上·南昌月考)将一副直角三角板如图1,摆放在直线上(直角三角板和直角三角板,),保持三角板不动,将三角板绕点以每秒的速度顺时针旋转,旋转时间为秒,当与射线重合时停止旋转.
(1)如图2,当为的角平分线时,求此时的值;
(2)当旋转至的内部时,求与的数量关系;
(3)在旋转过程中,当三角板的其中一边平行于三角板的某一边时,求此时t等于 (直接写出答案即可).
答案解析部分
1.【答案】C
【知识点】勾股定理;旋转的性质
2.【答案】D
【知识点】三角形内角和定理;等腰三角形的性质;旋转的性质
3.【答案】C
【知识点】平行线的性质;旋转的性质
4.【答案】B
【知识点】旋转的性质
5.【答案】D
【知识点】轴对称的性质;平移的性质;旋转的性质
6.【答案】C
【知识点】菱形的性质;旋转的性质;坐标与图形变化﹣旋转
7.【答案】B
【知识点】旋转对称图形
8.【答案】B
【知识点】旋转的性质
9.【答案】B
【知识点】点、线、面、体及之间的联系;图形的旋转
10.【答案】C
【知识点】勾股定理;平行四边形的性质;旋转的性质;等腰三角形的概念
11.【答案】圆柱
【知识点】图形的旋转
12.【答案】
【知识点】坐标与图形变化﹣旋转
13.【答案】17°
【知识点】旋转的性质
14.【答案】60
【知识点】生活中的旋转现象
15.【答案】6
【知识点】等边三角形的性质;旋转的性质
16.【答案】45°,75°,165°
【知识点】余角、补角及其性质;平行线的性质;图形的旋转
17.【答案】(1)
(2)或
(3)点P的坐标为:或或或.
【知识点】待定系数法求一次函数解析式;等腰三角形的判定与性质;旋转的性质
18.【答案】(1),
(2)
(3)
【知识点】点的坐标;勾股定理;旋转的性质;图形的平移
19.【答案】(1)
(2)或
(3)当时,;当时,
【知识点】角的运算;余角、补角及其性质;角平分线的性质;旋转的性质
20.【答案】或
【知识点】图形的旋转
21.【答案】(1)解:是等腰直角三角形,
∴,
,
∴,
∵是由旋转得到的,
∴,
∴,
∵,
∴
所以,
(2)解:,
理由:∵是由旋转得到的,
∴,
,
,
∴,(SAS)
∴.
【知识点】旋转的性质;三角形全等的判定-SAS
22.【答案】解:初步探究:△BCD的面积为 .
理由:如图②,过点D作BC的垂线,与BC的延长线交于点E.
∴∠BED=∠ACB=90°.
∵线段AB绕点B顺时针旋转90°得到线段BE,
∴AB=BD,∠ABD=90°.
∴∠ABC+∠DBE=90°.
∵∠A+∠ABC=90°.
∴∠A=∠DBE.
在△ABC和△BDE中,
,
∴△ABC≌△BDE(AAS)
∴BC=DE=a.
∵S△BCD= BC DE
∴S△BCD= ;
简单应用:如图③,过点A作AF⊥BC与F,过点D作DE⊥BC的延长线于点E,
∴∠AFB=∠E=90°,BF= BC= a.
∴∠FAB+∠ABF=90°.
∵∠ABD=90°,
∴∠ABF+∠DBE=90°,
∴∠FAB=∠EBD.
∵线段BD是由线段AB旋转得到的,
∴AB=BD.
在△AFB和△BED中,
,
∴△AFB≌△BED(AAS),
∴BF=DE= a.
∵S△BCD= BC DE,
∴S△BCD= a a= a2.
∴△BCD的面积为 .
【知识点】全等三角形的判定与性质;旋转的性质
23.【答案】(1)解:如图2,,
,
平分,
,
,
答:此时的值是;
(2)解:当旋转至的内部时,如图3,与的数量关系是:;
理由是:由旋转得:,
,
;
(3)或或或
【知识点】平行线的性质;旋转的性质
21世纪教育网(www.21cnjy.com)
2 / 12
23.1图形的旋转
一、单选题
1.(2022八下·贵阳期末)如图,在中,,,,将绕点顺时针旋转得到,点的对应点落在边上,连接,则的周长为( )
A. B. C. D.
2.(2025八下·连云港月考)如图,中,,.将绕点B逆时针旋转得到,使点C的对应点恰好落在边上,则的度数是( )
A. B. C. D.
3.(2021八下·北票期中)如图,在中,,将在平面内绕点逆时针旋转到的位置,且,则旋转角的度数为( )
A. B. C. D.
4.将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,得到数字“6”,现将数字“69”旋转180°,得到的数字是( )
A.96 B.69 C.66 D.99
5.(2024八上·上思月考)通过下列变换能得到全等图形的是( ).
A.只有平移 B.只有平移、旋转
C.只有平移、翻转 D.平移、旋转、翻转
6.(2024九上·蓬江期中)如图,菱形的对角线交于原点O,,.将菱形绕原点O逆时针旋转,每次旋转,则第2023次旋转结束时,点C的坐标为( )
A. B. C. D.
7.如图,该图形绕点O按下列角度旋转后,不能与其自身重合的是( )
A.72° B.108° C.144° D.216°
8.(2016·南山模拟)如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,此时点C恰好在线段DE上,若∠B=40°,∠CAE=60°,则∠DAC的度数为( )
A.15° B.20° C.25° D.30°
9.(2025七上·宜州期末)如图,沿图中虚线旋转一周,能围成的几何体是下面几何体中的( )
A. B. C. D.
10.(2023九上·临海月考)如图,平行四边形中,,,,是边上一点,且,是边上的一个动点,将线段绕点逆时针旋转,得到,连接、,则的最小值是( )
A.4 B. C. D.
二、填空题
11.(2024七上·高碑店月考)如图,一旋转门内部由三块玻璃隔板组成.将此旋转门旋转一周,能形成的几何体是 .
12.(2023八下·沿河月考)如图,把正方形铁片置于平面直角坐标系中,顶点A的坐标为,点在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转,第一次旋转至图①位置,第二次旋转至图②位置,…,则正方形铁片连续旋转2023次后,点P的坐标为 .
13.(2016·江西)如图所示,△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为 .
14.(2016九上·乌拉特前旗期中)钟表的时针匀速旋转一周需要12小时,经过2小时,时针旋转了 度.
15.(2024八上·上海市月考)在等边中,,点O在上,且,点P是上一动点,连接,将线段绕点O逆时针旋转得到线段.要使点D恰好落在边上,则的长是 .
16.(2024九上·信丰期末)如图,一副三角板的三个内角分别是90°,45°,45°和90°,60°,30°,按如图所示叠放在一起(点A,D,B在同一直线上),若固定△ABC,将△BDE绕着公共顶点B顺时针旋转α度(0<α<180),当边DE与△ABC的某一边平行时,相应的旋转角α的值为 .
三、计算题
17.(2023八上·沙坪坝期末)如图1,在平面直角坐标系中,直线:分别与x轴,y轴交于A,B两点,点C为x轴正半轴上一点,且,直线过点C且与y轴交于点D,与直线l1交于第二象限内的点E,已知点E到x轴的距离为.
(1)求点D的坐标;
(2)如图2,在直线上存在一点M,使,求出点M的坐标;
(3)如图3,将绕点O逆时针旋转得到,点P为直线上一动点,点Q为x轴上一动点,连接,,,当为以为腰的等腰直角三角形时,直接写出点P的坐标.
18.(2025九上·南昌期末)如图,图形中每一小格正方形的边长为1,已知.
(1)的长等于 ,的面积等于 ;
(2)将向右平移2个单位得到,则A点的对应点的坐标是 ;
(3)将绕点C按逆时针方向旋转后得到,则B点对应点的坐标是 .
19.(2025七上·锦江期末)如图1,点O为直线上一点,为射线,,将一个含角的直角三角尺的一个顶点放在点O处,直角边与直线重合.
(1)如图1,在内部,过点O作射线,使得,求的度数.
(2)将图1中的三角尺绕点O按每秒的速度沿逆时针方向旋转一周,射线平分,在旋转的过程中,是否存在某个时刻t(秒),使得,若存在,求出t的值,若不存在,请说明理由;
(3)如图2,平分,将三角尺绕点O按每秒的速度沿逆时针方向旋转,若射线从出发绕点O按每秒的速度沿逆时针方向旋转,设三角尺与射线运动时间为,在旋转过程中,若与始终满足(a与b为常数),求的值.
四、解答题
20.(2023七上·城关期中)长为4,宽为2的长方形绕其一边旋转构成一个圆柱的体积是多少?(结果保留π)
21.(2023九上·阜平期中)如图,在等腰直角三角形中,,是由绕点A按顺时针方向旋转得到的,连接.
(1)若,求旋转角的度数和的度数;
(2)判断与之间的数量关系,并说明理由.
22.(2017·农安模拟)问题原型:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.过点D作△BCD的BC边上的高DE,
易证△ABC≌△BDE,从而得到△BCD的面积为 .
初步探究:如图②,在Rt△ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.用含a的代数式表示△BCD的面积,并说明理由.
简单应用:如图③,在等腰三角形ABC中,AB=AC,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.直接写出△BCD的面积.(用含a的代数式表示)
23.(2023九上·南昌月考)将一副直角三角板如图1,摆放在直线上(直角三角板和直角三角板,),保持三角板不动,将三角板绕点以每秒的速度顺时针旋转,旋转时间为秒,当与射线重合时停止旋转.
(1)如图2,当为的角平分线时,求此时的值;
(2)当旋转至的内部时,求与的数量关系;
(3)在旋转过程中,当三角板的其中一边平行于三角板的某一边时,求此时t等于 (直接写出答案即可).
答案解析部分
1.【答案】C
【知识点】勾股定理;旋转的性质
2.【答案】D
【知识点】三角形内角和定理;等腰三角形的性质;旋转的性质
3.【答案】C
【知识点】平行线的性质;旋转的性质
4.【答案】B
【知识点】旋转的性质
5.【答案】D
【知识点】轴对称的性质;平移的性质;旋转的性质
6.【答案】C
【知识点】菱形的性质;旋转的性质;坐标与图形变化﹣旋转
7.【答案】B
【知识点】旋转对称图形
8.【答案】B
【知识点】旋转的性质
9.【答案】B
【知识点】点、线、面、体及之间的联系;图形的旋转
10.【答案】C
【知识点】勾股定理;平行四边形的性质;旋转的性质;等腰三角形的概念
11.【答案】圆柱
【知识点】图形的旋转
12.【答案】
【知识点】坐标与图形变化﹣旋转
13.【答案】17°
【知识点】旋转的性质
14.【答案】60
【知识点】生活中的旋转现象
15.【答案】6
【知识点】等边三角形的性质;旋转的性质
16.【答案】45°,75°,165°
【知识点】余角、补角及其性质;平行线的性质;图形的旋转
17.【答案】(1)
(2)或
(3)点P的坐标为:或或或.
【知识点】待定系数法求一次函数解析式;等腰三角形的判定与性质;旋转的性质
18.【答案】(1),
(2)
(3)
【知识点】点的坐标;勾股定理;旋转的性质;图形的平移
19.【答案】(1)
(2)或
(3)当时,;当时,
【知识点】角的运算;余角、补角及其性质;角平分线的性质;旋转的性质
20.【答案】或
【知识点】图形的旋转
21.【答案】(1)解:是等腰直角三角形,
∴,
,
∴,
∵是由旋转得到的,
∴,
∴,
∵,
∴
所以,
(2)解:,
理由:∵是由旋转得到的,
∴,
,
,
∴,(SAS)
∴.
【知识点】旋转的性质;三角形全等的判定-SAS
22.【答案】解:初步探究:△BCD的面积为 .
理由:如图②,过点D作BC的垂线,与BC的延长线交于点E.
∴∠BED=∠ACB=90°.
∵线段AB绕点B顺时针旋转90°得到线段BE,
∴AB=BD,∠ABD=90°.
∴∠ABC+∠DBE=90°.
∵∠A+∠ABC=90°.
∴∠A=∠DBE.
在△ABC和△BDE中,
,
∴△ABC≌△BDE(AAS)
∴BC=DE=a.
∵S△BCD= BC DE
∴S△BCD= ;
简单应用:如图③,过点A作AF⊥BC与F,过点D作DE⊥BC的延长线于点E,
∴∠AFB=∠E=90°,BF= BC= a.
∴∠FAB+∠ABF=90°.
∵∠ABD=90°,
∴∠ABF+∠DBE=90°,
∴∠FAB=∠EBD.
∵线段BD是由线段AB旋转得到的,
∴AB=BD.
在△AFB和△BED中,
,
∴△AFB≌△BED(AAS),
∴BF=DE= a.
∵S△BCD= BC DE,
∴S△BCD= a a= a2.
∴△BCD的面积为 .
【知识点】全等三角形的判定与性质;旋转的性质
23.【答案】(1)解:如图2,,
,
平分,
,
,
答:此时的值是;
(2)解:当旋转至的内部时,如图3,与的数量关系是:;
理由是:由旋转得:,
,
;
(3)或或或
【知识点】平行线的性质;旋转的性质
21世纪教育网(www.21cnjy.com)
2 / 12
同课章节目录
