23.2.1 中心对称 同步练习(含答案)
文档属性
| 名称 | 23.2.1 中心对称 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 889.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 21:33:50 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
23.2.1中心对称
一、单选题
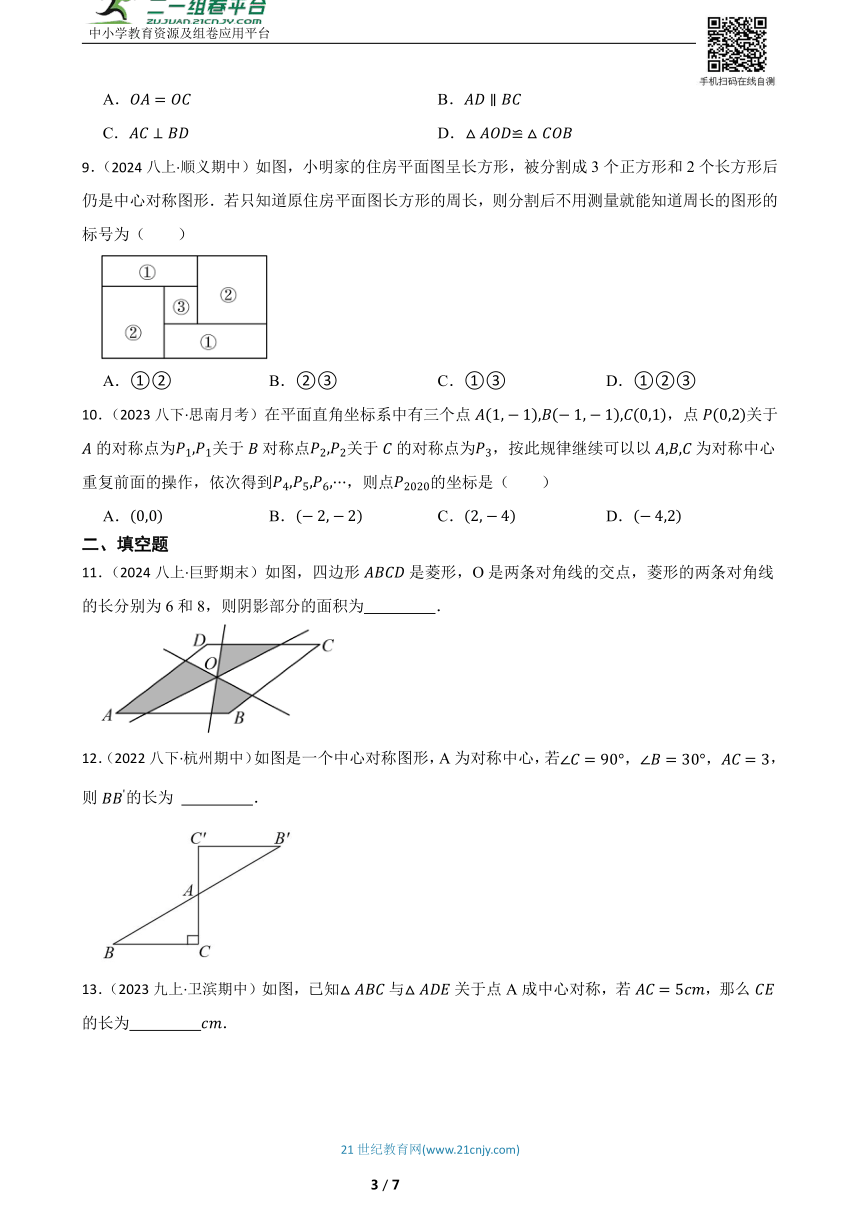
1.(2023九下·南昌月考)如图所示的是由个边长为1的小正方形网格组成,每个小正方形的顶点称为格点,的三个顶点,,均在格点上,将绕着边的中点旋转180°,下面说法不正确的是( )
A.各边的中点都可通过网格确定
B.绕的中点旋转后得到的三角形的顶点不在网格的格点上
C.旋转前后的两个三角形可形成平行四边形
D.绕着各边的中点旋转后得到的三角形的顶点都在网格的格点上
2.(2025九下·广州模拟)如图,在中,,点在轴上,将绕点旋转,点的对应点的坐标为( )
A. B. C. D.
3.(2024八下·碑林月考)以下说法中:①在同一平面内,可以把半径相等的两个圆中的一个看成是由另一个平移得到的;②经过旋转,对应线段平行且相等;③中心对称图形上的每一对对应点所连成的线段都被对称中心平分;④可以把两个全等图形中的一个看成是由另一个平移得到的.其中正确的有 ( )个.
A.4 B.3 C.2 D.1
4.(2023九上·津南期中)如图所示,△ABC与△A'B'C'是成中心对称的两个图形,则下列说法不正确的是( )
A.AB=A'B',BC=B'C' B.AB∥A'B',BC∥B'C'
C.S△ABC=S△A'B'C' D.△ABC≌△A'OC'
5.(2024九下·肥西开学考)下列交通标志中,是中心对称图形的是( )
A.禁止驶入 B.靠左侧道路行驶
C.向左和向右转弯 D. 环岛行驶
6.(2024七下·廊坊期中)如图所示,数轴上表示1,的点分别为,且两点到点A的距离相等,则点C所表示的数是( )
A. B. C. D.
7.(2023·石家庄模拟)如图,已知点A与点C关于点O对称,点B与点D也关于点O对称,若,.则AB的长可能是( )
A.3 B.4 C.7 D.11
8.(2024八下·瓯海期末)如图,与关于点 O 成中心对称,连接.下列结论不一定成立的是( )
A. B.
C. D.
9.(2024八上·顺义期中)如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )
A.①② B.②③ C.①③ D.①②③
10.(2023八下·思南月考)在平面直角坐标系中有三个点,点关于的对称点为关于对称点关于的对称点为,按此规律继续可以以为对称中心重复前面的操作,依次得到,则点的坐标是( )
A. B. C. D.
二、填空题
11.(2024八上·巨野期末)如图,四边形是菱形,O是两条对角线的交点,菱形的两条对角线的长分别为6和8,则阴影部分的面积为 .
12.(2022八下·杭州期中)如图是一个中心对称图形,A为对称中心,若,则的长为 .
13.(2023九上·卫滨期中)如图,已知与关于点A成中心对称,若,那么的长为 .
14.(2024八下·赫山期中)如图是一个中心对称图形,为对称中心,若,,,则的长为 .
15.(2024九上·四平期末)在方格纸中,选择标有序号的一个小正方形涂黑,与图中阴影构成中心对称图形,涂黑的小正方形序号为 ;若与图中阴影构成轴对称图形,涂黑的小正方形序号为 .
16.(2024八下·泉州期末)如图,在平面直角坐标系xOy中,菱形ABCD与菱形GFED关于点D成中心对称,点C,G在x轴的正半轴上,点A,F在反比例函数y=(k>0,x>0)的图象上,延长AB交x轴于点P(1,0),若∠APO=120°,则k的值是 .
三、解答题
17.(2024八下·徐州期末)如图,在方格纸中建立平面直角坐标系,与的顶点均为格点.
(1)若绕点逆时针旋转可得到,则旋转角至少为______;
(2)将绕点顺时针旋转得到,画出;
(3)若(2)中的与成中心对称,则对称中心的坐标为______.
18.(2024八下·新城月考)如图,与成中心对称,点O是它们的对称中心,若,,求的度数和的长度.
19.(2025九上·新余期末)(1)解方程:;
(2)如图,与关于点成中心对称,若,,,求的长.
20.(2025·船营模拟)已知抛物线经过点.点在这个抛物线上,当点不在轴上时,过点作轴于点,作线段关于坐标原点成中心对称的线段,设点的横坐标为.
(1)求此抛物线对应的函数解析式;
(2)当线段与线段在同一条直线上时,求线段的长度;
(3)当点在轴左侧时,若线段与此抛物线有且只有一个公共点,求的取值范围;
(4)作平行四边形.当边与此抛物线有两个公共点时,若以这两个公共点和点为顶点构造三角形的面积是面积的一半,直接写出的值.
答案解析部分
1.【答案】B
【知识点】平行四边形的判定;旋转的性质;两个图形成中心对称
2.【答案】C
【知识点】旋转的性质;中心对称的性质
3.【答案】C
【知识点】平移的性质;旋转的性质;两个图形成中心对称
4.【答案】D
【知识点】中心对称的性质
5.【答案】A
【知识点】两个图形成中心对称
6.【答案】D
【知识点】无理数在数轴上表示;中心对称的性质
7.【答案】C
【知识点】三角形三边关系;三角形全等的判定-SAS;中心对称的性质
8.【答案】C
【知识点】平行线的判定;三角形全等的判定-SAS;两个图形成中心对称
9.【答案】A
【知识点】中心对称的性质
10.【答案】B
【知识点】两个图形成中心对称
11.【答案】12
【知识点】菱形的性质;中心对称的性质
12.【答案】12
【知识点】含30°角的直角三角形;中心对称的性质
13.【答案】10
【知识点】三角形全等及其性质;中心对称的性质
14.【答案】
【知识点】中心对称的性质
15.【答案】②;⑤或⑥或⑦
【知识点】作图﹣中心对称
16.【答案】
【知识点】菱形的性质;中心对称的性质
17.【答案】(1)
(2)
(3)
【知识点】点的坐标;旋转的性质;作图﹣旋转;两个图形成中心对称
18.【答案】,
【知识点】中心对称的性质
19.【答案】(1),;(2).
【知识点】因式分解法解一元二次方程;三角形全等及其性质;勾股定理;中心对称的性质
20.【答案】(1);
(2)或;
(3)或;
(4)或.
【知识点】公式法解一元二次方程;待定系数法求二次函数解析式;中心对称的性质
21世纪教育网(www.21cnjy.com)
8 / 8
23.2.1中心对称
一、单选题
1.(2023九下·南昌月考)如图所示的是由个边长为1的小正方形网格组成,每个小正方形的顶点称为格点,的三个顶点,,均在格点上,将绕着边的中点旋转180°,下面说法不正确的是( )
A.各边的中点都可通过网格确定
B.绕的中点旋转后得到的三角形的顶点不在网格的格点上
C.旋转前后的两个三角形可形成平行四边形
D.绕着各边的中点旋转后得到的三角形的顶点都在网格的格点上
2.(2025九下·广州模拟)如图,在中,,点在轴上,将绕点旋转,点的对应点的坐标为( )
A. B. C. D.
3.(2024八下·碑林月考)以下说法中:①在同一平面内,可以把半径相等的两个圆中的一个看成是由另一个平移得到的;②经过旋转,对应线段平行且相等;③中心对称图形上的每一对对应点所连成的线段都被对称中心平分;④可以把两个全等图形中的一个看成是由另一个平移得到的.其中正确的有 ( )个.
A.4 B.3 C.2 D.1
4.(2023九上·津南期中)如图所示,△ABC与△A'B'C'是成中心对称的两个图形,则下列说法不正确的是( )
A.AB=A'B',BC=B'C' B.AB∥A'B',BC∥B'C'
C.S△ABC=S△A'B'C' D.△ABC≌△A'OC'
5.(2024九下·肥西开学考)下列交通标志中,是中心对称图形的是( )
A.禁止驶入 B.靠左侧道路行驶
C.向左和向右转弯 D. 环岛行驶
6.(2024七下·廊坊期中)如图所示,数轴上表示1,的点分别为,且两点到点A的距离相等,则点C所表示的数是( )
A. B. C. D.
7.(2023·石家庄模拟)如图,已知点A与点C关于点O对称,点B与点D也关于点O对称,若,.则AB的长可能是( )
A.3 B.4 C.7 D.11
8.(2024八下·瓯海期末)如图,与关于点 O 成中心对称,连接.下列结论不一定成立的是( )
A. B.
C. D.
9.(2024八上·顺义期中)如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )
A.①② B.②③ C.①③ D.①②③
10.(2023八下·思南月考)在平面直角坐标系中有三个点,点关于的对称点为关于对称点关于的对称点为,按此规律继续可以以为对称中心重复前面的操作,依次得到,则点的坐标是( )
A. B. C. D.
二、填空题
11.(2024八上·巨野期末)如图,四边形是菱形,O是两条对角线的交点,菱形的两条对角线的长分别为6和8,则阴影部分的面积为 .
12.(2022八下·杭州期中)如图是一个中心对称图形,A为对称中心,若,则的长为 .
13.(2023九上·卫滨期中)如图,已知与关于点A成中心对称,若,那么的长为 .
14.(2024八下·赫山期中)如图是一个中心对称图形,为对称中心,若,,,则的长为 .
15.(2024九上·四平期末)在方格纸中,选择标有序号的一个小正方形涂黑,与图中阴影构成中心对称图形,涂黑的小正方形序号为 ;若与图中阴影构成轴对称图形,涂黑的小正方形序号为 .
16.(2024八下·泉州期末)如图,在平面直角坐标系xOy中,菱形ABCD与菱形GFED关于点D成中心对称,点C,G在x轴的正半轴上,点A,F在反比例函数y=(k>0,x>0)的图象上,延长AB交x轴于点P(1,0),若∠APO=120°,则k的值是 .
三、解答题
17.(2024八下·徐州期末)如图,在方格纸中建立平面直角坐标系,与的顶点均为格点.
(1)若绕点逆时针旋转可得到,则旋转角至少为______;
(2)将绕点顺时针旋转得到,画出;
(3)若(2)中的与成中心对称,则对称中心的坐标为______.
18.(2024八下·新城月考)如图,与成中心对称,点O是它们的对称中心,若,,求的度数和的长度.
19.(2025九上·新余期末)(1)解方程:;
(2)如图,与关于点成中心对称,若,,,求的长.
20.(2025·船营模拟)已知抛物线经过点.点在这个抛物线上,当点不在轴上时,过点作轴于点,作线段关于坐标原点成中心对称的线段,设点的横坐标为.
(1)求此抛物线对应的函数解析式;
(2)当线段与线段在同一条直线上时,求线段的长度;
(3)当点在轴左侧时,若线段与此抛物线有且只有一个公共点,求的取值范围;
(4)作平行四边形.当边与此抛物线有两个公共点时,若以这两个公共点和点为顶点构造三角形的面积是面积的一半,直接写出的值.
答案解析部分
1.【答案】B
【知识点】平行四边形的判定;旋转的性质;两个图形成中心对称
2.【答案】C
【知识点】旋转的性质;中心对称的性质
3.【答案】C
【知识点】平移的性质;旋转的性质;两个图形成中心对称
4.【答案】D
【知识点】中心对称的性质
5.【答案】A
【知识点】两个图形成中心对称
6.【答案】D
【知识点】无理数在数轴上表示;中心对称的性质
7.【答案】C
【知识点】三角形三边关系;三角形全等的判定-SAS;中心对称的性质
8.【答案】C
【知识点】平行线的判定;三角形全等的判定-SAS;两个图形成中心对称
9.【答案】A
【知识点】中心对称的性质
10.【答案】B
【知识点】两个图形成中心对称
11.【答案】12
【知识点】菱形的性质;中心对称的性质
12.【答案】12
【知识点】含30°角的直角三角形;中心对称的性质
13.【答案】10
【知识点】三角形全等及其性质;中心对称的性质
14.【答案】
【知识点】中心对称的性质
15.【答案】②;⑤或⑥或⑦
【知识点】作图﹣中心对称
16.【答案】
【知识点】菱形的性质;中心对称的性质
17.【答案】(1)
(2)
(3)
【知识点】点的坐标;旋转的性质;作图﹣旋转;两个图形成中心对称
18.【答案】,
【知识点】中心对称的性质
19.【答案】(1),;(2).
【知识点】因式分解法解一元二次方程;三角形全等及其性质;勾股定理;中心对称的性质
20.【答案】(1);
(2)或;
(3)或;
(4)或.
【知识点】公式法解一元二次方程;待定系数法求二次函数解析式;中心对称的性质
21世纪教育网(www.21cnjy.com)
8 / 8
同课章节目录
