第23章 旋转 同步练习(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第23章旋转
一、单选题
1.(2025·凉州模拟)如图是一个由个相同的正方体组成的立体图形,它的三视图中是中心对称图形的是( )
A.主视图 B.左视图
C.俯视图 D.以上说法都不对
2.(2025九上·安州期末)如图,在的正方形网格中,绕某点旋转一定的角度,得到,则旋转中心是( )
A.点A B.点B C.点C D.点D
3.(2023九上·蓬江期中)2023年亚足联中国亚洲杯将于2023年6月16日至7月16日在北京、天津、上海、重庆、成都、西安、大连、青岛、厦门和苏州10座城市举行,这将是中国时隔19年后再次承办亚洲杯.下列是四届亚洲杯会徽的部分图案,其中既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
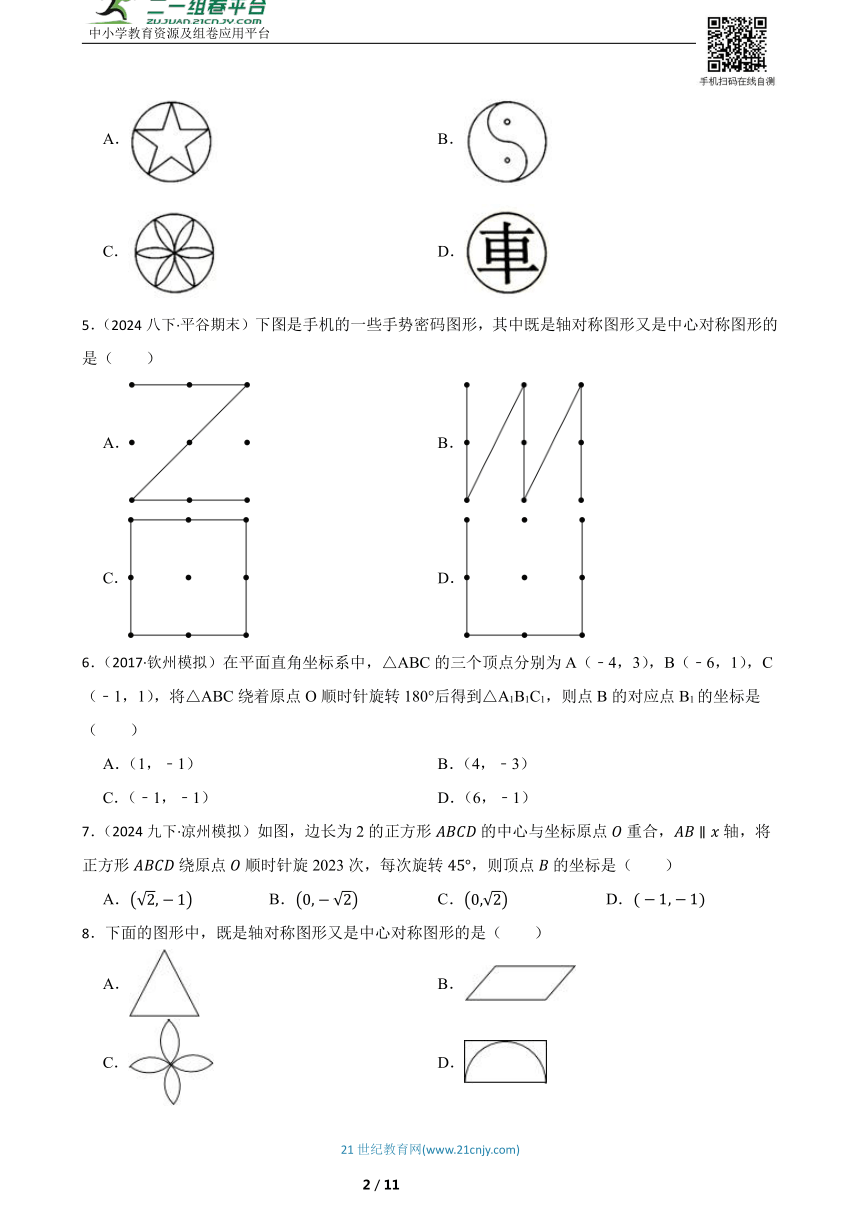
4.(2021九上·绥化期末)下列图形既是中心对称又是轴对称的是( )
A. B.
C. D.
5.(2024八下·平谷期末)下图是手机的一些手势密码图形,其中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
6.(2017·钦州模拟)在平面直角坐标系中,△ABC的三个顶点分别为A(﹣4,3),B(﹣6,1),C(﹣1,1),将△ABC绕着原点O顺时针旋转180°后得到△A1B1C1,则点B的对应点B1的坐标是( )
A.(1,﹣1) B.(4,﹣3)
C.(﹣1,﹣1) D.(6,﹣1)
7.(2024九下·凉州模拟)如图,边长为2的正方形的中心与坐标原点重合,轴,将正方形绕原点顺时针旋2023次,每次旋转,则顶点的坐标是( )
A. B. C. D.
8.下面的图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
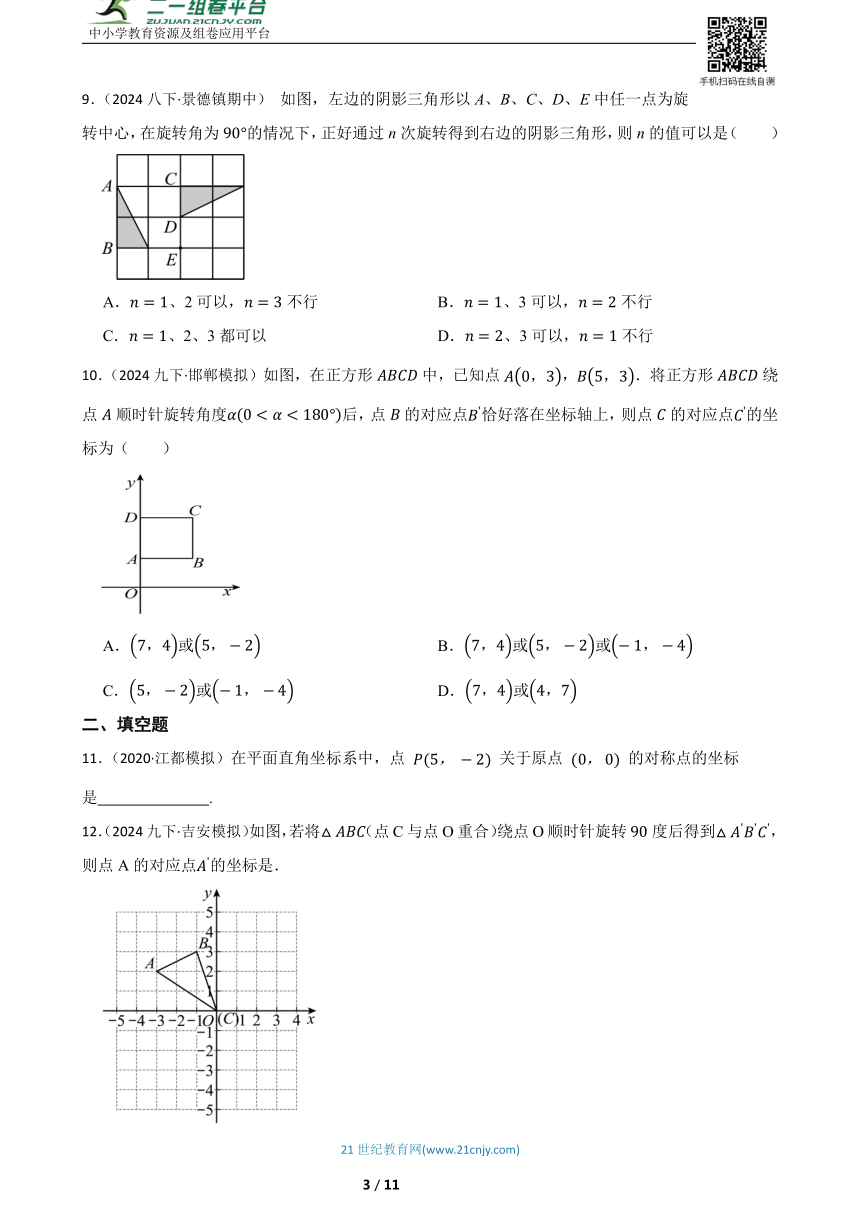
9.(2024八下·景德镇期中) 如图,左边的阴影三角形以A、B、C、D、E中任一点为旋转中心,在旋转角为的情况下,正好通过n次旋转得到右边的阴影三角形,则n的值可以是( )
A.、2可以,不行 B.、3可以,不行
C.、2、3都可以 D.、3可以,不行
10.(2024九下·邯郸模拟)如图,在正方形中,已知点,.将正方形绕点顺时针旋转角度后,点的对应点恰好落在坐标轴上,则点的对应点的坐标为( )
A.或 B.或或
C.或 D.或
二、填空题
11.(2020·江都模拟)在平面直角坐标系中,点 关于原点 的对称点的坐标是 .
12.(2024九下·吉安模拟)如图,若将(点C与点O重合)绕点O顺时针旋转度后得到,则点A的对应点的坐标是.
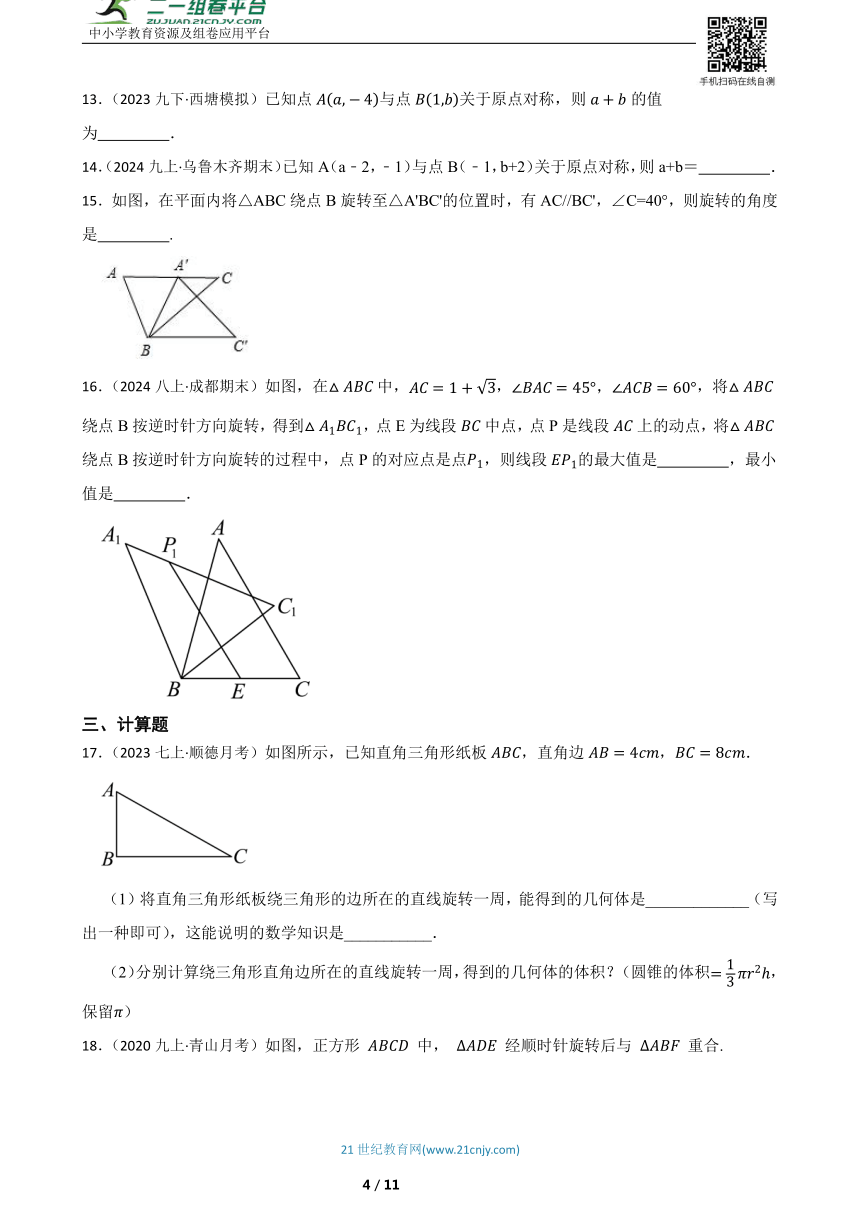
13.(2023九下·西塘模拟)已知点与点关于原点对称,则的值为 .
14.(2024九上·乌鲁木齐期末)已知A(a﹣2,﹣1)与点B(﹣1,b+2)关于原点对称,则a+b= .
15.如图,在平面内将△ABC绕点B旋转至△A'BC'的位置时,有AC//BC',∠C=40°,则旋转的角度是 .
16.(2024八上·成都期末)如图,在中,,,将绕点B按逆时针方向旋转,得到,点E为线段中点,点P是线段上的动点,将绕点B按逆时针方向旋转的过程中,点P的对应点是点,则线段的最大值是 ,最小值是 .
三、计算题
17.(2023七上·顺德月考)如图所示,已知直角三角形纸板,直角边,.
(1)将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到的几何体是_____________(写出一种即可),这能说明的数学知识是___________.
(2)分别计算绕三角形直角边所在的直线旋转一周,得到的几何体的体积?(圆锥的体积,保留)
18.(2020九上·青山月考)如图,正方形 中, 经顺时针旋转后与 重合.
(1)旋转中心是点 ,旋转了 度;
(2)如果 , ,求 的长.
四、解答题
19.如下图所示,利用关于原点对称的点的坐标特征,作出与线段AB关于原点对称的图形.
20.(2024九上·吉林期中)如图,在中,,,,将绕点A按顺时针旋转一定角度得到,当点B的对应点D恰好落在BC边上时,求CD的长.
21.(2019九上·崇阳期末)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)请画出将△ABC向下平移5个单位后得到的△A1B1C1;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.
22.(2024八上·镇海区期末)已知,,,将绕点顺时针旋转至,连结.
(1)如图1,当点落在线段上时,
①填空:______;______.
②作交于点,求线段的长度;
(2)如图2,若,求四边形的面积.
答案解析部分
1.【答案】C
【知识点】简单组合体的三视图;中心对称及中心对称图形
2.【答案】B
【知识点】旋转的性质
3.【答案】B
【知识点】轴对称图形;中心对称及中心对称图形
4.【答案】C
【知识点】轴对称图形;中心对称及中心对称图形
5.【答案】C
【知识点】轴对称图形;中心对称及中心对称图形
6.【答案】D
【知识点】坐标与图形变化﹣旋转
7.【答案】C
【知识点】勾股定理;坐标与图形变化﹣旋转
8.【答案】C
【知识点】轴对称图形;中心对称及中心对称图形
9.【答案】B
【知识点】旋转的性质
10.【答案】B
【知识点】坐标与图形性质;正方形的性质;旋转的性质
11.【答案】(-5,2)
【知识点】关于原点对称的点的坐标特征
12.【答案】
【知识点】点的坐标;作图﹣旋转
13.【答案】3
【知识点】关于原点对称的点的坐标特征
14.【答案】2
【知识点】关于原点对称的点的坐标特征
15.【答案】40°
【知识点】平行线的性质;图形的旋转
16.【答案】;
【知识点】含30°角的直角三角形;勾股定理;旋转的性质
17.【答案】(1)圆锥;面动成体;
(2);
【知识点】图形的旋转;已知展开图进行几何体的相关的计算
18.【答案】(1)A;90
(2)解:∵△ADE绕点A顺时针旋转90°后与△ABF重合,
∴BF=DE,S△ABF=S△ADE,
而CF=CB+BF=8,
∴BC+DE=8,
∵CE=CD-DE=BC-DE=4,
∴BC=6,
∴AC= BC=6 .
【知识点】正方形的性质;旋转的性质
19.【答案】解:作法:两个点关于原点对称时,它们坐标符号相反,即P(x,y)关于原点的对称点为P′(-x,-y),因此AB的两个端点A(1,3)、B(-2,1)关于原点的对称点分别为A′(-1,-3)、B′(2,-1),连结A′B′,就可得到与AB关于原点对称的A′B′.
【知识点】关于原点对称的点的坐标特征
20.【答案】1.6
【知识点】等边三角形的判定与性质;旋转的性质
21.【答案】(1)解:如图,△A1B1C1为所作;
(2)解:如图,△A2B2C2为所作,
OB=
点B旋转到点B2所经过的路径长=
【知识点】坐标与图形变化﹣旋转;作图﹣旋转
22.【答案】(1)①4,30
②过点作,如图,
∵,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
∵,
∴,
∴
(2)过点作,过点作,
∵旋转,
∴,
∴均为等边三角形,
∴,,
∴,
∵,
∴,
∵,,
∴,
∴,
∴,
∵,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴四边形的面积为
【知识点】等边三角形的判定与性质;勾股定理;旋转的性质
21世纪教育网(www.21cnjy.com)
2 / 11
第23章旋转
一、单选题
1.(2025·凉州模拟)如图是一个由个相同的正方体组成的立体图形,它的三视图中是中心对称图形的是( )
A.主视图 B.左视图
C.俯视图 D.以上说法都不对
2.(2025九上·安州期末)如图,在的正方形网格中,绕某点旋转一定的角度,得到,则旋转中心是( )
A.点A B.点B C.点C D.点D
3.(2023九上·蓬江期中)2023年亚足联中国亚洲杯将于2023年6月16日至7月16日在北京、天津、上海、重庆、成都、西安、大连、青岛、厦门和苏州10座城市举行,这将是中国时隔19年后再次承办亚洲杯.下列是四届亚洲杯会徽的部分图案,其中既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
4.(2021九上·绥化期末)下列图形既是中心对称又是轴对称的是( )
A. B.
C. D.
5.(2024八下·平谷期末)下图是手机的一些手势密码图形,其中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
6.(2017·钦州模拟)在平面直角坐标系中,△ABC的三个顶点分别为A(﹣4,3),B(﹣6,1),C(﹣1,1),将△ABC绕着原点O顺时针旋转180°后得到△A1B1C1,则点B的对应点B1的坐标是( )
A.(1,﹣1) B.(4,﹣3)
C.(﹣1,﹣1) D.(6,﹣1)
7.(2024九下·凉州模拟)如图,边长为2的正方形的中心与坐标原点重合,轴,将正方形绕原点顺时针旋2023次,每次旋转,则顶点的坐标是( )
A. B. C. D.
8.下面的图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
9.(2024八下·景德镇期中) 如图,左边的阴影三角形以A、B、C、D、E中任一点为旋转中心,在旋转角为的情况下,正好通过n次旋转得到右边的阴影三角形,则n的值可以是( )
A.、2可以,不行 B.、3可以,不行
C.、2、3都可以 D.、3可以,不行
10.(2024九下·邯郸模拟)如图,在正方形中,已知点,.将正方形绕点顺时针旋转角度后,点的对应点恰好落在坐标轴上,则点的对应点的坐标为( )
A.或 B.或或
C.或 D.或
二、填空题
11.(2020·江都模拟)在平面直角坐标系中,点 关于原点 的对称点的坐标是 .
12.(2024九下·吉安模拟)如图,若将(点C与点O重合)绕点O顺时针旋转度后得到,则点A的对应点的坐标是.
13.(2023九下·西塘模拟)已知点与点关于原点对称,则的值为 .
14.(2024九上·乌鲁木齐期末)已知A(a﹣2,﹣1)与点B(﹣1,b+2)关于原点对称,则a+b= .
15.如图,在平面内将△ABC绕点B旋转至△A'BC'的位置时,有AC//BC',∠C=40°,则旋转的角度是 .
16.(2024八上·成都期末)如图,在中,,,将绕点B按逆时针方向旋转,得到,点E为线段中点,点P是线段上的动点,将绕点B按逆时针方向旋转的过程中,点P的对应点是点,则线段的最大值是 ,最小值是 .
三、计算题
17.(2023七上·顺德月考)如图所示,已知直角三角形纸板,直角边,.
(1)将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到的几何体是_____________(写出一种即可),这能说明的数学知识是___________.
(2)分别计算绕三角形直角边所在的直线旋转一周,得到的几何体的体积?(圆锥的体积,保留)
18.(2020九上·青山月考)如图,正方形 中, 经顺时针旋转后与 重合.
(1)旋转中心是点 ,旋转了 度;
(2)如果 , ,求 的长.
四、解答题
19.如下图所示,利用关于原点对称的点的坐标特征,作出与线段AB关于原点对称的图形.
20.(2024九上·吉林期中)如图,在中,,,,将绕点A按顺时针旋转一定角度得到,当点B的对应点D恰好落在BC边上时,求CD的长.
21.(2019九上·崇阳期末)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)请画出将△ABC向下平移5个单位后得到的△A1B1C1;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.
22.(2024八上·镇海区期末)已知,,,将绕点顺时针旋转至,连结.
(1)如图1,当点落在线段上时,
①填空:______;______.
②作交于点,求线段的长度;
(2)如图2,若,求四边形的面积.
答案解析部分
1.【答案】C
【知识点】简单组合体的三视图;中心对称及中心对称图形
2.【答案】B
【知识点】旋转的性质
3.【答案】B
【知识点】轴对称图形;中心对称及中心对称图形
4.【答案】C
【知识点】轴对称图形;中心对称及中心对称图形
5.【答案】C
【知识点】轴对称图形;中心对称及中心对称图形
6.【答案】D
【知识点】坐标与图形变化﹣旋转
7.【答案】C
【知识点】勾股定理;坐标与图形变化﹣旋转
8.【答案】C
【知识点】轴对称图形;中心对称及中心对称图形
9.【答案】B
【知识点】旋转的性质
10.【答案】B
【知识点】坐标与图形性质;正方形的性质;旋转的性质
11.【答案】(-5,2)
【知识点】关于原点对称的点的坐标特征
12.【答案】
【知识点】点的坐标;作图﹣旋转
13.【答案】3
【知识点】关于原点对称的点的坐标特征
14.【答案】2
【知识点】关于原点对称的点的坐标特征
15.【答案】40°
【知识点】平行线的性质;图形的旋转
16.【答案】;
【知识点】含30°角的直角三角形;勾股定理;旋转的性质
17.【答案】(1)圆锥;面动成体;
(2);
【知识点】图形的旋转;已知展开图进行几何体的相关的计算
18.【答案】(1)A;90
(2)解:∵△ADE绕点A顺时针旋转90°后与△ABF重合,
∴BF=DE,S△ABF=S△ADE,
而CF=CB+BF=8,
∴BC+DE=8,
∵CE=CD-DE=BC-DE=4,
∴BC=6,
∴AC= BC=6 .
【知识点】正方形的性质;旋转的性质
19.【答案】解:作法:两个点关于原点对称时,它们坐标符号相反,即P(x,y)关于原点的对称点为P′(-x,-y),因此AB的两个端点A(1,3)、B(-2,1)关于原点的对称点分别为A′(-1,-3)、B′(2,-1),连结A′B′,就可得到与AB关于原点对称的A′B′.
【知识点】关于原点对称的点的坐标特征
20.【答案】1.6
【知识点】等边三角形的判定与性质;旋转的性质
21.【答案】(1)解:如图,△A1B1C1为所作;
(2)解:如图,△A2B2C2为所作,
OB=
点B旋转到点B2所经过的路径长=
【知识点】坐标与图形变化﹣旋转;作图﹣旋转
22.【答案】(1)①4,30
②过点作,如图,
∵,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
∵,
∴,
∴
(2)过点作,过点作,
∵旋转,
∴,
∴均为等边三角形,
∴,,
∴,
∵,
∴,
∵,,
∴,
∴,
∴,
∵,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴四边形的面积为
【知识点】等边三角形的判定与性质;勾股定理;旋转的性质
21世纪教育网(www.21cnjy.com)
2 / 11
同课章节目录
