2024-2025学年广东省湛江市雷州市八年级(下)期末数学试卷(含详解)
文档属性
| 名称 | 2024-2025学年广东省湛江市雷州市八年级(下)期末数学试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 20:56:22 | ||
图片预览




文档简介
2024-2025学年广东省湛江市雷州市八年级(下)期末数学试卷
一、单选题(每小题3分,共30分)
1.(3分)下列二次根式中,是最简二次根式的是( )
A. B. C. D.
2.(3分)以下列各数为边长,能构成直角三角形的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
3.(3分)某科技论坛对Deep Seek、豆包、腾讯元宝、夸克四款AI助手中某一项功能的月度用户评分进行了统计,数据如表所示(单位:分):
AI助手 评分(满分100)
Deep Seek 88
豆包 84
腾讯元宝 84
夸克 86
评分的众数和中位数分别是( )
A.84,86 B.84,88 C.88,85 D.84,85
4.(3分)若添加一个条件,使得 ABCD是菱形,则这个条件可以是( )
A.AB=CD B.AC=BD C.AC⊥BD D.AB⊥BC
5.(3分)下列函数中,y是x的正比例函数的是( )
A.y=x﹣1 B. C.y=2x2 D.y=3x
6.(3分)下列计算正确的是( )
A. B.
C. D.
7.(3分)如图,长方形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
A. B. C. D.2.5
8.(3分)若点A(﹣2,y1),B(3,y2),C(1,y3)在一次函数y=﹣3x+m(m是常数)的图象上,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y2>y1>y3 C.y1>y3>y2 D.y3>y2>y1
9.(3分)对于一次函数y=2x﹣1,下列结论不正确的是( )
A.它的图象与y轴交于点(0,﹣1)
B.y随x的增大而增大
C.当时,y>0
D.它的图象经过第一、二、三象限
10.(3分)如图,在菱形ABCD中,对角线AC,BD相交于点O,点E是AD的中点,连接OE,若AC=6,BD=8,则下列结论错误的是( )
A.AB=5 B.
C.菱形的面积为48 D.点A到BC的距离为
二、填空题(每小题3分,共15分)
11.(3分)代数式在实数范围内有意义时,x应满足的条件是 .
12.(3分)某校为调查学生对2023年播出的《感动中国》节目中英雄人物事迹的了解情况,选取甲、乙、丙三个班级进行“感动中国故事知多少”的问卷测试,若甲、乙、丙三个班级的平均分相同,且方差分别为S甲2=5.48,S乙2=5.32,S丙2=5.17,则甲、乙、丙三个班级中成比较稳定的是 班.(填“甲”或“乙”或“丙”)
13.(3分)如图,已知直线y1=2x+3与直线y2=kx+b(k≠0)交于点(n,6),则关于x的不等式kx+b≥2x+3的解集为 .
14.(3分)如图,平行四边形ABCD的对角线AC,BD交于点E,F是DC的中点,若EF=2,则BC= .
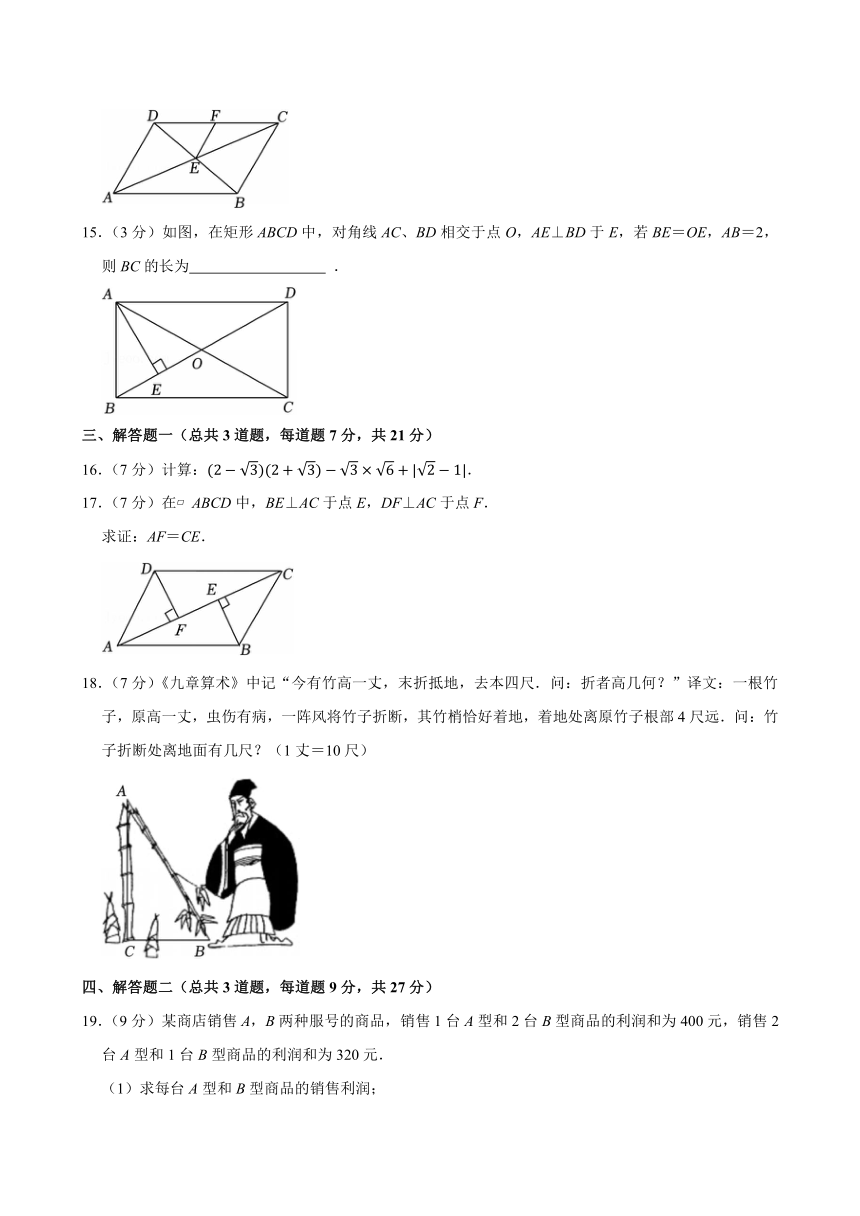
15.(3分)如图,在矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD于E,若BE=OE,AB=2,则BC的长为 .
三、解答题一(总共3道题,每道题7分,共21分)
16.(7分)计算:.
17.(7分)在 ABCD中,BE⊥AC于点E,DF⊥AC于点F.
求证:AF=CE.
18.(7分)《九章算术》中记“今有竹高一丈,末折抵地,去本四尺.问:折者高几何?”译文:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好着地,着地处离原竹子根部4尺远.问:竹子折断处离地面有几尺?(1丈=10尺)
四、解答题二(总共3道题,每道题9分,共27分)
19.(9分)某商店销售A,B两种服号的商品,销售1台A型和2台B型商品的利润和为400元,销售2台A型和1台B型商品的利润和为320元.
(1)求每台A型和B型商品的销售利润;
(2)商店计划购进A,B两种型号的商品共10台,其中A型商品数量不少于B型商品数量的一半,设购进A型商品m台,这10台商品的销售总利润为w元,求该商店购进A,B两种型号的商品各多少台,才能使销售总利润最大?
20.(9分)如图,在四边形ABCD中,AD∥BC,BC=DC,CA平分∠BCD,过点A作AE⊥CB,交CB延长线于点E.四边形ABCD对角线AC,BD交于点O,连接EO.
(1)求证:四边形ABCD是菱形;
(2)若OE=1,∠BCD=60°,求△AEC的面积.
21.(9分)2025年春节,《哪吒之魔童闹海》(以下简称《哪吒2》)横空出世,现已登顶全球动画电影票房榜,米小果同学为了了解这部电影在同学中的受欢迎程度,在初三年级随机抽取了10名男生和10名女生展开问卷调查,并对数据进行整理,描述和分析(评分分数用x表示,共分为四组:
A.x<70;B.70≤x<80;C.80≤x<90;D.90≤x≤100),下面给出了部分信息:
10名女生对《哪吒2》的评分分数:67,77,79,83,89,91,98,98,98,100.
10名男生对《哪吒2》的评分分数在C组的数据是:82,83,86.
20名同学对《哪吒2》评分统计表
性别 平均数 众数 中位数 方差 满分占比
女生 88 a 90 112.2 10%
男生 88 100 b 200.2 50%
根据以上信息,解答下列问题:
(1)上述图表中的a= ,b= ,m= ;
(2)根据以上数据分析,你认为是女生更喜欢《哪吒2》还是男生更喜欢?请说明理由;(写出一条理由即可)
(3)我校初三年级有400名女生和500名男生去看过《哪吒2》,估计这些学生中对《哪吒2》的评分在D组共有多少人?
五、解答题三(总共2道题,22题13分,23题14分,共27分)
22.(13分)如图,已知直线y=kx+b经过A(6,0)、B(0,3)两点.
(1)求直线y=kx+b的解析式;
(2)若C是线段OA上一点,将线段CB绕点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上.
①求点C和点D的坐标;
②若点P在y轴上,Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点Q坐标,否则说明理由.
23.(14分)如图正方形ABCD中,点E为对角线AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F.
(1)求证:EF=ED;
(2)若AB=2,,BF的长度为 ;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.
2024-2025学年广东省湛江市雷州市八年级(下)期末数学试卷
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 D C D C D B C C D C
一、单选题(每小题3分,共30分)
1.(3分)下列二次根式中,是最简二次根式的是( )
A. B. C. D.
【解答】解:A.,故不是最简二次根式,不符合题意;
B.,故不是最简二次根式,不符合题意;
C.,故不是最简二次根式,不符合题意;
D. 是最简二次根式,符合题意.
故选:D.
2.(3分)以下列各数为边长,能构成直角三角形的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
【解答】解:A、因为12+22≠32,所以不能构成直角三角形;
B、因为22+32≠42,所以不能构成直角三角形;
C、因为32+42=52,所以能构成直角三角形;
D、因为42+52≠62,所以不能构成直角三角形.
故选:C.
3.(3分)某科技论坛对Deep Seek、豆包、腾讯元宝、夸克四款AI助手中某一项功能的月度用户评分进行了统计,数据如表所示(单位:分):
AI助手 评分(满分100)
Deep Seek 88
豆包 84
腾讯元宝 84
夸克 86
评分的众数和中位数分别是( )
A.84,86 B.84,88 C.88,85 D.84,85
【解答】解:数据按照从小到大排列是:84,84,86,88,
84出现次数最多,
故众数是84,中位数是,
故选:D.
4.(3分)若添加一个条件,使得 ABCD是菱形,则这个条件可以是( )
A.AB=CD B.AC=BD C.AC⊥BD D.AB⊥BC
【解答】解:A选项, ABCD中有AB=CD,添加该条件不能证明 ABCD是菱形,A不符合题意,
B选项,添加AC=BD后可证 ABCD是矩形,但不能证明 ABCD是菱形,不符合题意,
C选项,添加AC=BD后可证 ABCD是菱形,符合题意,
D选项,添加AC=BD后可证 ABCD是矩形,但不能证明 ABCD是菱形,不符合题意,
故选:C.
5.(3分)下列函数中,y是x的正比例函数的是( )
A.y=x﹣1 B. C.y=2x2 D.y=3x
【解答】解:A、y=x﹣1是一次函数,不符合题意;
B、y是反比例函数.不符合题意;
C、y=2x2是二次函数,不符合题意;
D、y=3x是正比例函数,符合题意.
故选:D.
6.(3分)下列计算正确的是( )
A. B.
C. D.
【解答】解:根据二次根式加减法、乘除法的法则逐项分析判断如下:
A、和,不是同类二次根式,不能合并,故选项A错误;
B、,故选项B正确;
C、,故选项C错误;
D、,故选项D错误;
故选:B.
7.(3分)如图,长方形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
A. B. C. D.2.5
【解答】解:∵四边形OABC是矩形,
∴∠OAB=90°,
∴OB,
∴这个点表示的示数是,
故选:C.
8.(3分)若点A(﹣2,y1),B(3,y2),C(1,y3)在一次函数y=﹣3x+m(m是常数)的图象上,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y2>y1>y3 C.y1>y3>y2 D.y3>y2>y1
【解答】解:∵k=﹣3<0,
∴y随x的增大而减小,
又∵点A(﹣2,y1),B(3,y2),C(1,y3)在一次函数y=﹣3x+m(m是常数)的图象上,且﹣2<1<3,
∴y1>y3>y2.
故选:C.
9.(3分)对于一次函数y=2x﹣1,下列结论不正确的是( )
A.它的图象与y轴交于点(0,﹣1)
B.y随x的增大而增大
C.当时,y>0
D.它的图象经过第一、二、三象限
【解答】解:A.当x=0时,y=﹣1,则它的图象与y轴交于点(0,﹣1),故本选项不符合题意;
B.∵k=2>0,
∴y随x的增大而增大,故本选项不符合题意;
C.当时,y>0,故本选项不符合题意;
D.它的图象经过第二、三,四象限,故本选项符合题意;
故选:D.
10.(3分)如图,在菱形ABCD中,对角线AC,BD相交于点O,点E是AD的中点,连接OE,若AC=6,BD=8,则下列结论错误的是( )
A.AB=5 B.
C.菱形的面积为48 D.点A到BC的距离为
【解答】解:A、由题意可得:
∴AC⊥BD,且,,
则在Rt△AOB中,∠AOB=90°,OA=3,OB=4,由勾股定理可知,
故该选项正确,不符合题意;
B、由题意可得:AC⊥BD,且,,
则在Rt△AOD中,∠AOD=90°,OA=3,OD=4,由勾股定理可知,
∵点E是Rt△AOD斜边AD的中点,
∴,
故该选项正确,不符合题意;
C、在菱形ABCD中,AC=6,BD=8,则菱形的面积为,
故该选项错误,符合题意;
D、过点A作AF⊥BC于点F,如图所示:
∴由等面积可知,
由题意可得:
∴AC⊥BD,且,,
则在Rt△BOC中,∠BOC=90°,OB=3,OC=4,由勾股定理可知,
∴24=5AF,解得,
则点A到BC的距离为,
故该选项正确,不符合题意;
故选:C.
二、填空题(每小题3分,共15分)
11.(3分)代数式在实数范围内有意义时,x应满足的条件是 x≥5 .
【解答】解:∵代数式在实数范围内有意义,
∴x﹣5≥0,
∴x≥5.
故答案为:x≥5.
12.(3分)某校为调查学生对2023年播出的《感动中国》节目中英雄人物事迹的了解情况,选取甲、乙、丙三个班级进行“感动中国故事知多少”的问卷测试,若甲、乙、丙三个班级的平均分相同,且方差分别为S甲2=5.48,S乙2=5.32,S丙2=5.17,则甲、乙、丙三个班级中成比较稳定的是 丙 班.(填“甲”或“乙”或“丙”)
【解答】解:∵三个班级的平均分相同,S甲2>S乙2>S丙2,
∴三个班级中成比较稳定的是丙.
故答案为:丙.
13.(3分)如图,已知直线y1=2x+3与直线y2=kx+b(k≠0)交于点(n,6),则关于x的不等式kx+b≥2x+3的解集为 x .
【解答】解:将点(n,6)代入y=2x+3得,
n,
由函数图象可知,
当x时,一次函数y1=2x+3的图象不在一次函数y2=kx+b图象的上方,即kx+b≥2x+3,
所以关于x的不等式kx+b≥2x+3的解集为:x.
故答案为:x.
14.(3分)如图,平行四边形ABCD的对角线AC,BD交于点E,F是DC的中点,若EF=2,则BC= 4 .
【解答】解:∵平行四边形ABCD的对角线AC,BD交于点E,F是DC的中点,EF=2,
∴E是BD的中点,
∴EF是△BCD的中位线,
∴2,
∴BC=4,
故答案为:4.
15.(3分)如图,在矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD于E,若BE=OE,AB=2,则BC的长为 2 .
【解答】解:∵四边形ABCD是矩形,
∴AO=OB,
∵AE⊥BD于E,BE=EO,
∴△ABO是等边三角形,
∴AB=BO=2,
∴AC=2OB=4,
∴BC2,
故答案为:2.
三、解答题一(总共3道题,每道题7分,共21分)
16.(7分)计算:.
【解答】解:原式=4﹣31
=1﹣31
=﹣2.
17.(7分)在 ABCD中,BE⊥AC于点E,DF⊥AC于点F.
求证:AF=CE.
【解答】证明:∵四边形ABCD是平行四边形,
∴AD∥CB,AD=CB,
∴∠DAF=∠BCE
∵BE⊥AC,DF⊥AC,
∴∠DFA=∠BEC=90°
∴△ADF≌△CBE(AAS),
∴AF=CE.
18.(7分)《九章算术》中记“今有竹高一丈,末折抵地,去本四尺.问:折者高几何?”译文:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好着地,着地处离原竹子根部4尺远.问:竹子折断处离地面有几尺?(1丈=10尺)
【解答】解:设竹子折断处离地面有x尺,
由题意得:∠C=90°,BC=4尺,AC+AB=10尺,AC=x尺,
∴AB=(10﹣x)尺,
在直角三角形ABC中,由勾股定理得:AC2+BC2=AB2,
∴x2+42=(10﹣x)2,
解得:x=4.2.
答:竹子折断处离地面有4.2尺.
四、解答题二(总共3道题,每道题9分,共27分)
19.(9分)某商店销售A,B两种服号的商品,销售1台A型和2台B型商品的利润和为400元,销售2台A型和1台B型商品的利润和为320元.
(1)求每台A型和B型商品的销售利润;
(2)商店计划购进A,B两种型号的商品共10台,其中A型商品数量不少于B型商品数量的一半,设购进A型商品m台,这10台商品的销售总利润为w元,求该商店购进A,B两种型号的商品各多少台,才能使销售总利润最大?
【解答】解:(1)设A型利润x元/台,B型利润y元/台,由“销售1台A型和2台B型商品的利润和为400元,销售2台A型和1台B型商品的利润和为320元”可得:
,
∴
答:A型利润80元/台,B型利润160元/台;
(2)设A型m台,则B型(10﹣m)台,
∴,
∴,W=80m+160(10﹣m),
∴W=﹣80m+1600,
∵k=﹣80<0,
∴W随m增大而减小,
∴当m=4时,Wmin=﹣80×4+1600=1280,
答:A型4台,B型6台,总利润最大.
20.(9分)如图,在四边形ABCD中,AD∥BC,BC=DC,CA平分∠BCD,过点A作AE⊥CB,交CB延长线于点E.四边形ABCD对角线AC,BD交于点O,连接EO.
(1)求证:四边形ABCD是菱形;
(2)若OE=1,∠BCD=60°,求△AEC的面积.
【解答】(1)证明:由题意可得:
∴∠CAD=∠ACB,∠ACD=∠ACB,
∴∠ACD=∠CAD,
∴AD=CD,
∵BC=DC,
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形;
∵BC=DC,
∴四边形ABCD是菱形;
(2)解:由题意可得:AC⊥BD,,
∵AE⊥CB,
∴∠AEC=90°,
∴,
∴AC=2,
∴,
∴△AEC的面积.
21.(9分)2025年春节,《哪吒之魔童闹海》(以下简称《哪吒2》)横空出世,现已登顶全球动画电影票房榜,米小果同学为了了解这部电影在同学中的受欢迎程度,在初三年级随机抽取了10名男生和10名女生展开问卷调查,并对数据进行整理,描述和分析(评分分数用x表示,共分为四组:
A.x<70;B.70≤x<80;C.80≤x<90;D.90≤x≤100),下面给出了部分信息:
10名女生对《哪吒2》的评分分数:67,77,79,83,89,91,98,98,98,100.
10名男生对《哪吒2》的评分分数在C组的数据是:82,83,86.
20名同学对《哪吒2》评分统计表
性别 平均数 众数 中位数 方差 满分占比
女生 88 a 90 112.2 10%
男生 88 100 b 200.2 50%
根据以上信息,解答下列问题:
(1)上述图表中的a= 98 ,b= 93 ,m= 10 ;
(2)根据以上数据分析,你认为是女生更喜欢《哪吒2》还是男生更喜欢?请说明理由;(写出一条理由即可)
(3)我校初三年级有400名女生和500名男生去看过《哪吒2》,估计这些学生中对《哪吒2》的评分在D组共有多少人?
【解答】解:(1)10名女生对《哪吒2》的评分分数:67,77,79,83,89,91,98,98,98,100.
98出现最多,则a=98,
根据统计表可得满分的有10×50%=5人,则中位数为第5和第6个数据,数据是:82,83,86.
则按从小到大排列,第5个数据为86,第6个数据为100,
则,
评分分数为A和B的人数和为10﹣10×50%﹣3=2,都不为0,
∴评分分数为A和B的人数都是1人,
∴,则m=10,
故答案为:98,93,10.
(2)男生更喜欢《哪吒2》,
根据中位数和众数分析,男生的中位数和众数都比女生的高,因此,男生更喜欢《哪吒2》,
(3)(人).
答:估计这些学生中对《哪吒2》的评分在D组共有450人.
五、解答题三(总共2道题,22题13分,23题14分,共27分)
22.(13分)如图,已知直线y=kx+b经过A(6,0)、B(0,3)两点.
(1)求直线y=kx+b的解析式;
(2)若C是线段OA上一点,将线段CB绕点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上.
①求点C和点D的坐标;
②若点P在y轴上,Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点Q坐标,否则说明理由.
【解答】解:(1)将A(6,0),B(0,3)代入y=kx+b得:
,解得:,
∴直线AB的表达式为yx+3;
(2)①∵∠BOC=∠BCD=∠CED=90°,
∴∠OCB+∠DCE=90°,∠DCE+∠CDE=90°,
∴∠BCO=∠CDE.
在△BOC和△CED中,
,
∴△BOC≌△CED(AAS),
∴OC=DE,BO=CE=3.
设OC=DE=m,则点D的坐标为(m+3,m),
∵点D在直线AB上,
∴m(m+3)+3,
∴m=1,
∴点C的坐标为(1,0),点D的坐标为(4,1);
②存在,设点Q的坐标为(n,n+3).
分两种情况考虑,
当CD为边时,
∵点C的坐标为(1,0),点D的坐标为(4,1),点P的横坐标为0,
∴0﹣n=4﹣1或n﹣0=4﹣1,
∴n=﹣3或n=3,
∴点Q的坐标为(3,)或(﹣3,);
当CD为对角线时,
∵点C的坐标为(1,0),点D的坐标为(4,1),点P的横坐标为0,
∴n+0=1+4,
∴n=5,
∴点Q″的坐标为(5,).
综上所述:存在以C、D、P、Q为顶点的四边形是平行四边形,点Q的坐标为(3,)或(﹣3,)或(5,).
23.(14分)如图正方形ABCD中,点E为对角线AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F.
(1)求证:EF=ED;
(2)若AB=2,,BF的长度为 2 ;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.
【解答】(1)证明:过点E作EM⊥AD于点M,ME的延长线交BC于点N,EH⊥AB于点H,如图1所示:
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠B=∠BCD=∠CDA=90°,∠BAD=∠DAC=45°,AD∥BC,
∴EN⊥BC,
∴四边形ABNM,四边形CDMN和四边形AMEH都是矩形,
∴∠FNE=∠EMD=90°,MN=AB=AD,AM=BN,
∴∠1+∠2=90°,
∵EF⊥DE,
∴∠1+∠3=90°,
∴∠3=∠2,
∵EM⊥AD,∠DAC=45°,
∴△AME是等腰直角三角形,
∴AM=EM,
∵MN=AD,
∴EM+EN=DM+AM,
∴EN=DM,
在△ENF和△DME中,
,
∴△ENF≌△DME(AAS),
∴EF=ED;
(2)解:∵四边形ABCD是正方形,且AB=2,
∴AD=AB=2,
设AM=EM=BN=a,
∴DM=AD﹣AM=2﹣a,
在△DME中,由勾股定理得:EM2+DM2=DE2,
∴,
整理得:a2﹣2a+1=0,
解得:a=1,
∴AM=EM=BN=a=1,
∵△ENF≌△DME,
∴FN=EM=1,
∴BF=BN+FN=2,
故答案为:2;
(3)∵点E为对角线AC上一点,
∴线段DE与正方形ABCD的某条边的夹角是30°时,有以下两种情况:
①当DE与AD的夹角是30°时,即∠ADE=30°,如图3①所示:
∴∠EDC=∠CDA﹣∠ADE=60°,
∵EF⊥DE,
∴∠DEF=90°,
在四边形DEFC中,∠EFC+∠BCD+∠EDC+∠DEF=360°,
∴∠EFC+90°+60°+90°=360°,
∴∠EFC=120°;
②当DE与BC的夹角是30°时,即∠CDE=30°,如图3②所示:
∵四边形ABCD是正方形,
∴∠DCA=∠BCA=45°,
在△CDE中,∠CED=180°﹣(∠CDE+∠DCA)=180°﹣(30°+45°)=105°,
∵EF⊥DE,
∴∠DEF=90°,
∴∠CEF=∠CED﹣∠DEF=105°﹣90°=15°,
∵∠BCA是△CEF的外角,
∴∠BCA=∠CEF+∠EFC,
∴45°=15°+∠EFC,
∴∠EFC=30°,
综上所述:∠EFC的度数是120°或30°.
一、单选题(每小题3分,共30分)
1.(3分)下列二次根式中,是最简二次根式的是( )
A. B. C. D.
2.(3分)以下列各数为边长,能构成直角三角形的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
3.(3分)某科技论坛对Deep Seek、豆包、腾讯元宝、夸克四款AI助手中某一项功能的月度用户评分进行了统计,数据如表所示(单位:分):
AI助手 评分(满分100)
Deep Seek 88
豆包 84
腾讯元宝 84
夸克 86
评分的众数和中位数分别是( )
A.84,86 B.84,88 C.88,85 D.84,85
4.(3分)若添加一个条件,使得 ABCD是菱形,则这个条件可以是( )
A.AB=CD B.AC=BD C.AC⊥BD D.AB⊥BC
5.(3分)下列函数中,y是x的正比例函数的是( )
A.y=x﹣1 B. C.y=2x2 D.y=3x
6.(3分)下列计算正确的是( )
A. B.
C. D.
7.(3分)如图,长方形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
A. B. C. D.2.5
8.(3分)若点A(﹣2,y1),B(3,y2),C(1,y3)在一次函数y=﹣3x+m(m是常数)的图象上,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y2>y1>y3 C.y1>y3>y2 D.y3>y2>y1
9.(3分)对于一次函数y=2x﹣1,下列结论不正确的是( )
A.它的图象与y轴交于点(0,﹣1)
B.y随x的增大而增大
C.当时,y>0
D.它的图象经过第一、二、三象限
10.(3分)如图,在菱形ABCD中,对角线AC,BD相交于点O,点E是AD的中点,连接OE,若AC=6,BD=8,则下列结论错误的是( )
A.AB=5 B.
C.菱形的面积为48 D.点A到BC的距离为
二、填空题(每小题3分,共15分)
11.(3分)代数式在实数范围内有意义时,x应满足的条件是 .
12.(3分)某校为调查学生对2023年播出的《感动中国》节目中英雄人物事迹的了解情况,选取甲、乙、丙三个班级进行“感动中国故事知多少”的问卷测试,若甲、乙、丙三个班级的平均分相同,且方差分别为S甲2=5.48,S乙2=5.32,S丙2=5.17,则甲、乙、丙三个班级中成比较稳定的是 班.(填“甲”或“乙”或“丙”)
13.(3分)如图,已知直线y1=2x+3与直线y2=kx+b(k≠0)交于点(n,6),则关于x的不等式kx+b≥2x+3的解集为 .
14.(3分)如图,平行四边形ABCD的对角线AC,BD交于点E,F是DC的中点,若EF=2,则BC= .
15.(3分)如图,在矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD于E,若BE=OE,AB=2,则BC的长为 .
三、解答题一(总共3道题,每道题7分,共21分)
16.(7分)计算:.
17.(7分)在 ABCD中,BE⊥AC于点E,DF⊥AC于点F.
求证:AF=CE.
18.(7分)《九章算术》中记“今有竹高一丈,末折抵地,去本四尺.问:折者高几何?”译文:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好着地,着地处离原竹子根部4尺远.问:竹子折断处离地面有几尺?(1丈=10尺)
四、解答题二(总共3道题,每道题9分,共27分)
19.(9分)某商店销售A,B两种服号的商品,销售1台A型和2台B型商品的利润和为400元,销售2台A型和1台B型商品的利润和为320元.
(1)求每台A型和B型商品的销售利润;
(2)商店计划购进A,B两种型号的商品共10台,其中A型商品数量不少于B型商品数量的一半,设购进A型商品m台,这10台商品的销售总利润为w元,求该商店购进A,B两种型号的商品各多少台,才能使销售总利润最大?
20.(9分)如图,在四边形ABCD中,AD∥BC,BC=DC,CA平分∠BCD,过点A作AE⊥CB,交CB延长线于点E.四边形ABCD对角线AC,BD交于点O,连接EO.
(1)求证:四边形ABCD是菱形;
(2)若OE=1,∠BCD=60°,求△AEC的面积.
21.(9分)2025年春节,《哪吒之魔童闹海》(以下简称《哪吒2》)横空出世,现已登顶全球动画电影票房榜,米小果同学为了了解这部电影在同学中的受欢迎程度,在初三年级随机抽取了10名男生和10名女生展开问卷调查,并对数据进行整理,描述和分析(评分分数用x表示,共分为四组:
A.x<70;B.70≤x<80;C.80≤x<90;D.90≤x≤100),下面给出了部分信息:
10名女生对《哪吒2》的评分分数:67,77,79,83,89,91,98,98,98,100.
10名男生对《哪吒2》的评分分数在C组的数据是:82,83,86.
20名同学对《哪吒2》评分统计表
性别 平均数 众数 中位数 方差 满分占比
女生 88 a 90 112.2 10%
男生 88 100 b 200.2 50%
根据以上信息,解答下列问题:
(1)上述图表中的a= ,b= ,m= ;
(2)根据以上数据分析,你认为是女生更喜欢《哪吒2》还是男生更喜欢?请说明理由;(写出一条理由即可)
(3)我校初三年级有400名女生和500名男生去看过《哪吒2》,估计这些学生中对《哪吒2》的评分在D组共有多少人?
五、解答题三(总共2道题,22题13分,23题14分,共27分)
22.(13分)如图,已知直线y=kx+b经过A(6,0)、B(0,3)两点.
(1)求直线y=kx+b的解析式;
(2)若C是线段OA上一点,将线段CB绕点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上.
①求点C和点D的坐标;
②若点P在y轴上,Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点Q坐标,否则说明理由.
23.(14分)如图正方形ABCD中,点E为对角线AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F.
(1)求证:EF=ED;
(2)若AB=2,,BF的长度为 ;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.
2024-2025学年广东省湛江市雷州市八年级(下)期末数学试卷
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 D C D C D B C C D C
一、单选题(每小题3分,共30分)
1.(3分)下列二次根式中,是最简二次根式的是( )
A. B. C. D.
【解答】解:A.,故不是最简二次根式,不符合题意;
B.,故不是最简二次根式,不符合题意;
C.,故不是最简二次根式,不符合题意;
D. 是最简二次根式,符合题意.
故选:D.
2.(3分)以下列各数为边长,能构成直角三角形的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
【解答】解:A、因为12+22≠32,所以不能构成直角三角形;
B、因为22+32≠42,所以不能构成直角三角形;
C、因为32+42=52,所以能构成直角三角形;
D、因为42+52≠62,所以不能构成直角三角形.
故选:C.
3.(3分)某科技论坛对Deep Seek、豆包、腾讯元宝、夸克四款AI助手中某一项功能的月度用户评分进行了统计,数据如表所示(单位:分):
AI助手 评分(满分100)
Deep Seek 88
豆包 84
腾讯元宝 84
夸克 86
评分的众数和中位数分别是( )
A.84,86 B.84,88 C.88,85 D.84,85
【解答】解:数据按照从小到大排列是:84,84,86,88,
84出现次数最多,
故众数是84,中位数是,
故选:D.
4.(3分)若添加一个条件,使得 ABCD是菱形,则这个条件可以是( )
A.AB=CD B.AC=BD C.AC⊥BD D.AB⊥BC
【解答】解:A选项, ABCD中有AB=CD,添加该条件不能证明 ABCD是菱形,A不符合题意,
B选项,添加AC=BD后可证 ABCD是矩形,但不能证明 ABCD是菱形,不符合题意,
C选项,添加AC=BD后可证 ABCD是菱形,符合题意,
D选项,添加AC=BD后可证 ABCD是矩形,但不能证明 ABCD是菱形,不符合题意,
故选:C.
5.(3分)下列函数中,y是x的正比例函数的是( )
A.y=x﹣1 B. C.y=2x2 D.y=3x
【解答】解:A、y=x﹣1是一次函数,不符合题意;
B、y是反比例函数.不符合题意;
C、y=2x2是二次函数,不符合题意;
D、y=3x是正比例函数,符合题意.
故选:D.
6.(3分)下列计算正确的是( )
A. B.
C. D.
【解答】解:根据二次根式加减法、乘除法的法则逐项分析判断如下:
A、和,不是同类二次根式,不能合并,故选项A错误;
B、,故选项B正确;
C、,故选项C错误;
D、,故选项D错误;
故选:B.
7.(3分)如图,长方形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
A. B. C. D.2.5
【解答】解:∵四边形OABC是矩形,
∴∠OAB=90°,
∴OB,
∴这个点表示的示数是,
故选:C.
8.(3分)若点A(﹣2,y1),B(3,y2),C(1,y3)在一次函数y=﹣3x+m(m是常数)的图象上,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y2>y1>y3 C.y1>y3>y2 D.y3>y2>y1
【解答】解:∵k=﹣3<0,
∴y随x的增大而减小,
又∵点A(﹣2,y1),B(3,y2),C(1,y3)在一次函数y=﹣3x+m(m是常数)的图象上,且﹣2<1<3,
∴y1>y3>y2.
故选:C.
9.(3分)对于一次函数y=2x﹣1,下列结论不正确的是( )
A.它的图象与y轴交于点(0,﹣1)
B.y随x的增大而增大
C.当时,y>0
D.它的图象经过第一、二、三象限
【解答】解:A.当x=0时,y=﹣1,则它的图象与y轴交于点(0,﹣1),故本选项不符合题意;
B.∵k=2>0,
∴y随x的增大而增大,故本选项不符合题意;
C.当时,y>0,故本选项不符合题意;
D.它的图象经过第二、三,四象限,故本选项符合题意;
故选:D.
10.(3分)如图,在菱形ABCD中,对角线AC,BD相交于点O,点E是AD的中点,连接OE,若AC=6,BD=8,则下列结论错误的是( )
A.AB=5 B.
C.菱形的面积为48 D.点A到BC的距离为
【解答】解:A、由题意可得:
∴AC⊥BD,且,,
则在Rt△AOB中,∠AOB=90°,OA=3,OB=4,由勾股定理可知,
故该选项正确,不符合题意;
B、由题意可得:AC⊥BD,且,,
则在Rt△AOD中,∠AOD=90°,OA=3,OD=4,由勾股定理可知,
∵点E是Rt△AOD斜边AD的中点,
∴,
故该选项正确,不符合题意;
C、在菱形ABCD中,AC=6,BD=8,则菱形的面积为,
故该选项错误,符合题意;
D、过点A作AF⊥BC于点F,如图所示:
∴由等面积可知,
由题意可得:
∴AC⊥BD,且,,
则在Rt△BOC中,∠BOC=90°,OB=3,OC=4,由勾股定理可知,
∴24=5AF,解得,
则点A到BC的距离为,
故该选项正确,不符合题意;
故选:C.
二、填空题(每小题3分,共15分)
11.(3分)代数式在实数范围内有意义时,x应满足的条件是 x≥5 .
【解答】解:∵代数式在实数范围内有意义,
∴x﹣5≥0,
∴x≥5.
故答案为:x≥5.
12.(3分)某校为调查学生对2023年播出的《感动中国》节目中英雄人物事迹的了解情况,选取甲、乙、丙三个班级进行“感动中国故事知多少”的问卷测试,若甲、乙、丙三个班级的平均分相同,且方差分别为S甲2=5.48,S乙2=5.32,S丙2=5.17,则甲、乙、丙三个班级中成比较稳定的是 丙 班.(填“甲”或“乙”或“丙”)
【解答】解:∵三个班级的平均分相同,S甲2>S乙2>S丙2,
∴三个班级中成比较稳定的是丙.
故答案为:丙.
13.(3分)如图,已知直线y1=2x+3与直线y2=kx+b(k≠0)交于点(n,6),则关于x的不等式kx+b≥2x+3的解集为 x .
【解答】解:将点(n,6)代入y=2x+3得,
n,
由函数图象可知,
当x时,一次函数y1=2x+3的图象不在一次函数y2=kx+b图象的上方,即kx+b≥2x+3,
所以关于x的不等式kx+b≥2x+3的解集为:x.
故答案为:x.
14.(3分)如图,平行四边形ABCD的对角线AC,BD交于点E,F是DC的中点,若EF=2,则BC= 4 .
【解答】解:∵平行四边形ABCD的对角线AC,BD交于点E,F是DC的中点,EF=2,
∴E是BD的中点,
∴EF是△BCD的中位线,
∴2,
∴BC=4,
故答案为:4.
15.(3分)如图,在矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD于E,若BE=OE,AB=2,则BC的长为 2 .
【解答】解:∵四边形ABCD是矩形,
∴AO=OB,
∵AE⊥BD于E,BE=EO,
∴△ABO是等边三角形,
∴AB=BO=2,
∴AC=2OB=4,
∴BC2,
故答案为:2.
三、解答题一(总共3道题,每道题7分,共21分)
16.(7分)计算:.
【解答】解:原式=4﹣31
=1﹣31
=﹣2.
17.(7分)在 ABCD中,BE⊥AC于点E,DF⊥AC于点F.
求证:AF=CE.
【解答】证明:∵四边形ABCD是平行四边形,
∴AD∥CB,AD=CB,
∴∠DAF=∠BCE
∵BE⊥AC,DF⊥AC,
∴∠DFA=∠BEC=90°
∴△ADF≌△CBE(AAS),
∴AF=CE.
18.(7分)《九章算术》中记“今有竹高一丈,末折抵地,去本四尺.问:折者高几何?”译文:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好着地,着地处离原竹子根部4尺远.问:竹子折断处离地面有几尺?(1丈=10尺)
【解答】解:设竹子折断处离地面有x尺,
由题意得:∠C=90°,BC=4尺,AC+AB=10尺,AC=x尺,
∴AB=(10﹣x)尺,
在直角三角形ABC中,由勾股定理得:AC2+BC2=AB2,
∴x2+42=(10﹣x)2,
解得:x=4.2.
答:竹子折断处离地面有4.2尺.
四、解答题二(总共3道题,每道题9分,共27分)
19.(9分)某商店销售A,B两种服号的商品,销售1台A型和2台B型商品的利润和为400元,销售2台A型和1台B型商品的利润和为320元.
(1)求每台A型和B型商品的销售利润;
(2)商店计划购进A,B两种型号的商品共10台,其中A型商品数量不少于B型商品数量的一半,设购进A型商品m台,这10台商品的销售总利润为w元,求该商店购进A,B两种型号的商品各多少台,才能使销售总利润最大?
【解答】解:(1)设A型利润x元/台,B型利润y元/台,由“销售1台A型和2台B型商品的利润和为400元,销售2台A型和1台B型商品的利润和为320元”可得:
,
∴
答:A型利润80元/台,B型利润160元/台;
(2)设A型m台,则B型(10﹣m)台,
∴,
∴,W=80m+160(10﹣m),
∴W=﹣80m+1600,
∵k=﹣80<0,
∴W随m增大而减小,
∴当m=4时,Wmin=﹣80×4+1600=1280,
答:A型4台,B型6台,总利润最大.
20.(9分)如图,在四边形ABCD中,AD∥BC,BC=DC,CA平分∠BCD,过点A作AE⊥CB,交CB延长线于点E.四边形ABCD对角线AC,BD交于点O,连接EO.
(1)求证:四边形ABCD是菱形;
(2)若OE=1,∠BCD=60°,求△AEC的面积.
【解答】(1)证明:由题意可得:
∴∠CAD=∠ACB,∠ACD=∠ACB,
∴∠ACD=∠CAD,
∴AD=CD,
∵BC=DC,
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形;
∵BC=DC,
∴四边形ABCD是菱形;
(2)解:由题意可得:AC⊥BD,,
∵AE⊥CB,
∴∠AEC=90°,
∴,
∴AC=2,
∴,
∴△AEC的面积.
21.(9分)2025年春节,《哪吒之魔童闹海》(以下简称《哪吒2》)横空出世,现已登顶全球动画电影票房榜,米小果同学为了了解这部电影在同学中的受欢迎程度,在初三年级随机抽取了10名男生和10名女生展开问卷调查,并对数据进行整理,描述和分析(评分分数用x表示,共分为四组:
A.x<70;B.70≤x<80;C.80≤x<90;D.90≤x≤100),下面给出了部分信息:
10名女生对《哪吒2》的评分分数:67,77,79,83,89,91,98,98,98,100.
10名男生对《哪吒2》的评分分数在C组的数据是:82,83,86.
20名同学对《哪吒2》评分统计表
性别 平均数 众数 中位数 方差 满分占比
女生 88 a 90 112.2 10%
男生 88 100 b 200.2 50%
根据以上信息,解答下列问题:
(1)上述图表中的a= 98 ,b= 93 ,m= 10 ;
(2)根据以上数据分析,你认为是女生更喜欢《哪吒2》还是男生更喜欢?请说明理由;(写出一条理由即可)
(3)我校初三年级有400名女生和500名男生去看过《哪吒2》,估计这些学生中对《哪吒2》的评分在D组共有多少人?
【解答】解:(1)10名女生对《哪吒2》的评分分数:67,77,79,83,89,91,98,98,98,100.
98出现最多,则a=98,
根据统计表可得满分的有10×50%=5人,则中位数为第5和第6个数据,数据是:82,83,86.
则按从小到大排列,第5个数据为86,第6个数据为100,
则,
评分分数为A和B的人数和为10﹣10×50%﹣3=2,都不为0,
∴评分分数为A和B的人数都是1人,
∴,则m=10,
故答案为:98,93,10.
(2)男生更喜欢《哪吒2》,
根据中位数和众数分析,男生的中位数和众数都比女生的高,因此,男生更喜欢《哪吒2》,
(3)(人).
答:估计这些学生中对《哪吒2》的评分在D组共有450人.
五、解答题三(总共2道题,22题13分,23题14分,共27分)
22.(13分)如图,已知直线y=kx+b经过A(6,0)、B(0,3)两点.
(1)求直线y=kx+b的解析式;
(2)若C是线段OA上一点,将线段CB绕点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上.
①求点C和点D的坐标;
②若点P在y轴上,Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点Q坐标,否则说明理由.
【解答】解:(1)将A(6,0),B(0,3)代入y=kx+b得:
,解得:,
∴直线AB的表达式为yx+3;
(2)①∵∠BOC=∠BCD=∠CED=90°,
∴∠OCB+∠DCE=90°,∠DCE+∠CDE=90°,
∴∠BCO=∠CDE.
在△BOC和△CED中,
,
∴△BOC≌△CED(AAS),
∴OC=DE,BO=CE=3.
设OC=DE=m,则点D的坐标为(m+3,m),
∵点D在直线AB上,
∴m(m+3)+3,
∴m=1,
∴点C的坐标为(1,0),点D的坐标为(4,1);
②存在,设点Q的坐标为(n,n+3).
分两种情况考虑,
当CD为边时,
∵点C的坐标为(1,0),点D的坐标为(4,1),点P的横坐标为0,
∴0﹣n=4﹣1或n﹣0=4﹣1,
∴n=﹣3或n=3,
∴点Q的坐标为(3,)或(﹣3,);
当CD为对角线时,
∵点C的坐标为(1,0),点D的坐标为(4,1),点P的横坐标为0,
∴n+0=1+4,
∴n=5,
∴点Q″的坐标为(5,).
综上所述:存在以C、D、P、Q为顶点的四边形是平行四边形,点Q的坐标为(3,)或(﹣3,)或(5,).
23.(14分)如图正方形ABCD中,点E为对角线AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F.
(1)求证:EF=ED;
(2)若AB=2,,BF的长度为 2 ;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.
【解答】(1)证明:过点E作EM⊥AD于点M,ME的延长线交BC于点N,EH⊥AB于点H,如图1所示:
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠B=∠BCD=∠CDA=90°,∠BAD=∠DAC=45°,AD∥BC,
∴EN⊥BC,
∴四边形ABNM,四边形CDMN和四边形AMEH都是矩形,
∴∠FNE=∠EMD=90°,MN=AB=AD,AM=BN,
∴∠1+∠2=90°,
∵EF⊥DE,
∴∠1+∠3=90°,
∴∠3=∠2,
∵EM⊥AD,∠DAC=45°,
∴△AME是等腰直角三角形,
∴AM=EM,
∵MN=AD,
∴EM+EN=DM+AM,
∴EN=DM,
在△ENF和△DME中,
,
∴△ENF≌△DME(AAS),
∴EF=ED;
(2)解:∵四边形ABCD是正方形,且AB=2,
∴AD=AB=2,
设AM=EM=BN=a,
∴DM=AD﹣AM=2﹣a,
在△DME中,由勾股定理得:EM2+DM2=DE2,
∴,
整理得:a2﹣2a+1=0,
解得:a=1,
∴AM=EM=BN=a=1,
∵△ENF≌△DME,
∴FN=EM=1,
∴BF=BN+FN=2,
故答案为:2;
(3)∵点E为对角线AC上一点,
∴线段DE与正方形ABCD的某条边的夹角是30°时,有以下两种情况:
①当DE与AD的夹角是30°时,即∠ADE=30°,如图3①所示:
∴∠EDC=∠CDA﹣∠ADE=60°,
∵EF⊥DE,
∴∠DEF=90°,
在四边形DEFC中,∠EFC+∠BCD+∠EDC+∠DEF=360°,
∴∠EFC+90°+60°+90°=360°,
∴∠EFC=120°;
②当DE与BC的夹角是30°时,即∠CDE=30°,如图3②所示:
∵四边形ABCD是正方形,
∴∠DCA=∠BCA=45°,
在△CDE中,∠CED=180°﹣(∠CDE+∠DCA)=180°﹣(30°+45°)=105°,
∵EF⊥DE,
∴∠DEF=90°,
∴∠CEF=∠CED﹣∠DEF=105°﹣90°=15°,
∵∠BCA是△CEF的外角,
∴∠BCA=∠CEF+∠EFC,
∴45°=15°+∠EFC,
∴∠EFC=30°,
综上所述:∠EFC的度数是120°或30°.
同课章节目录
