2016秋《学练优》冀教版九年级数学上册课件 第24章24.3一元二次方程根与系数的关系 (共16张PPT)
文档属性
| 名称 | 2016秋《学练优》冀教版九年级数学上册课件 第24章24.3一元二次方程根与系数的关系 (共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-06 19:51:29 | ||
图片预览






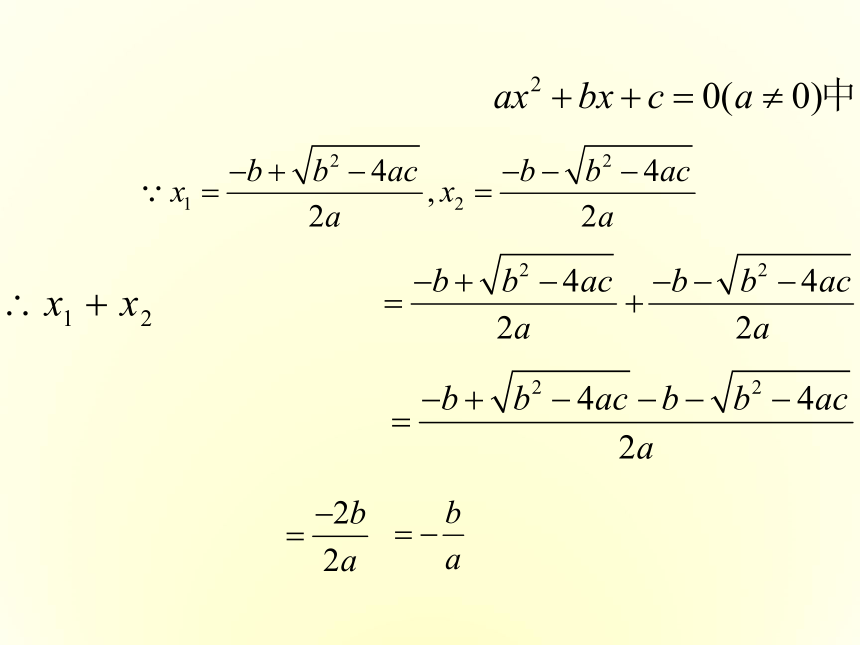
文档简介
课件16张PPT。24.3 一元二次方程根与系数的关系*导入新课讲授新课当堂练习课堂小结第二十四章 解一元二次方程 1.复习一元二次方程的根的判别式和求根公式.
2.理解并掌握一元二次方程根与系数的关系. (重点)
3.能够运用一元二次方程根与系数的关系解决问题.(难点)问题1 导入新课求根公式是什么?根的个数怎么确定的?一元二次方程的解法有哪些,步骤呢?知识回顾问题2 讲授新课 问题1:你发现这些一元二次方程的两根x1+ x2与x1 ? x2系数有什么规律?2 132-1 3 2-31 4 54-2问题2 x1+ x2,x1?x2与系数有什么规律? 猜想:当二次项系数为1时,方程 x2+px+q=0的两根为x1, x2.
如果一元二次方程ax2+bx+c=0(a、b、c是常数且a≠0)的两根为x1、x2,则:
x1+x2和x1.x2与系数a,b,c 的关系.拓广探索韦达定理的两个重要推论:推论1:如果方程x2+px+q=0的两个根是x1,x2,那么x1+x2=-p,x1·x2=q.推论2:以两个数x1,x2为根的一元二次方程(二次项系数为1)是x2-(x1+x2)·x+x1·x2=0类型一 直接运用根与系数的关系例1 不解方程,求下列方程两根的和与积.典例精析在使用根与系数的关系时,应注意:
⑴不是一般式的要先化成一般式;
⑵在使用x1+x2=- 时,注意“- ”不要漏写.类型二 求关于两根的对称式或代数式的值典例精析例2 不解方程,求方程2x2+3x-1=0的两根的平方和、倒数和.解:根据根与系数的关系可知: 类型三 求方程中字母系数的值例3 已知方程3x2-18x+m=0的一个根是1,求它的另一个根及m的值.解:设方程 3x2-18x+m=0的两个根分别是x1、x2,其中x1=1.
所以:x1 + x2=1+x2=6,
即:x2=5 .
由于x1·x2=1×5=
得:m=15.
答:方程的另一个根是5,m=15.典例精析当堂练习 1.方程 有一个正根,一个负根,求m的取值范围.解:由已知, Δ=即m>0;
m-1<0.∴0 (1)求k的值; (2)求(x1-x2)2的值.解:(1)根据根与系数的关系
所以(x1+1)(x2+1)=x1x2+(x1+x2)+1=
解得:k=-7;
(2)因为k=-7,所以
则:课堂小结任何一个一元二次方程的根与系数的关系:如果方程ax2+bx+c=0(a≠0)的两个根是x1 , x2 ,那么x1 + x2= , x1 ·x2= -一元二次方程的根与系数的关系(韦达定理)注:能用根与系数的关系的前提条件为b2-4ac≥0
2.理解并掌握一元二次方程根与系数的关系. (重点)
3.能够运用一元二次方程根与系数的关系解决问题.(难点)问题1 导入新课求根公式是什么?根的个数怎么确定的?一元二次方程的解法有哪些,步骤呢?知识回顾问题2 讲授新课 问题1:你发现这些一元二次方程的两根x1+ x2与x1 ? x2系数有什么规律?2 132-1 3 2-31 4 54-2问题2 x1+ x2,x1?x2与系数有什么规律? 猜想:当二次项系数为1时,方程 x2+px+q=0的两根为x1, x2.
如果一元二次方程ax2+bx+c=0(a、b、c是常数且a≠0)的两根为x1、x2,则:
x1+x2和x1.x2与系数a,b,c 的关系.拓广探索韦达定理的两个重要推论:推论1:如果方程x2+px+q=0的两个根是x1,x2,那么x1+x2=-p,x1·x2=q.推论2:以两个数x1,x2为根的一元二次方程(二次项系数为1)是x2-(x1+x2)·x+x1·x2=0类型一 直接运用根与系数的关系例1 不解方程,求下列方程两根的和与积.典例精析在使用根与系数的关系时,应注意:
⑴不是一般式的要先化成一般式;
⑵在使用x1+x2=- 时,注意“- ”不要漏写.类型二 求关于两根的对称式或代数式的值典例精析例2 不解方程,求方程2x2+3x-1=0的两根的平方和、倒数和.解:根据根与系数的关系可知: 类型三 求方程中字母系数的值例3 已知方程3x2-18x+m=0的一个根是1,求它的另一个根及m的值.解:设方程 3x2-18x+m=0的两个根分别是x1、x2,其中x1=1.
所以:x1 + x2=1+x2=6,
即:x2=5 .
由于x1·x2=1×5=
得:m=15.
答:方程的另一个根是5,m=15.典例精析当堂练习 1.方程 有一个正根,一个负根,求m的取值范围.解:由已知, Δ=即m>0;
m-1<0.∴0
所以(x1+1)(x2+1)=x1x2+(x1+x2)+1=
解得:k=-7;
(2)因为k=-7,所以
则:课堂小结任何一个一元二次方程的根与系数的关系:如果方程ax2+bx+c=0(a≠0)的两个根是x1 , x2 ,那么x1 + x2= , x1 ·x2= -一元二次方程的根与系数的关系(韦达定理)注:能用根与系数的关系的前提条件为b2-4ac≥0
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
