3.1.2 指数函数 课件 (2)

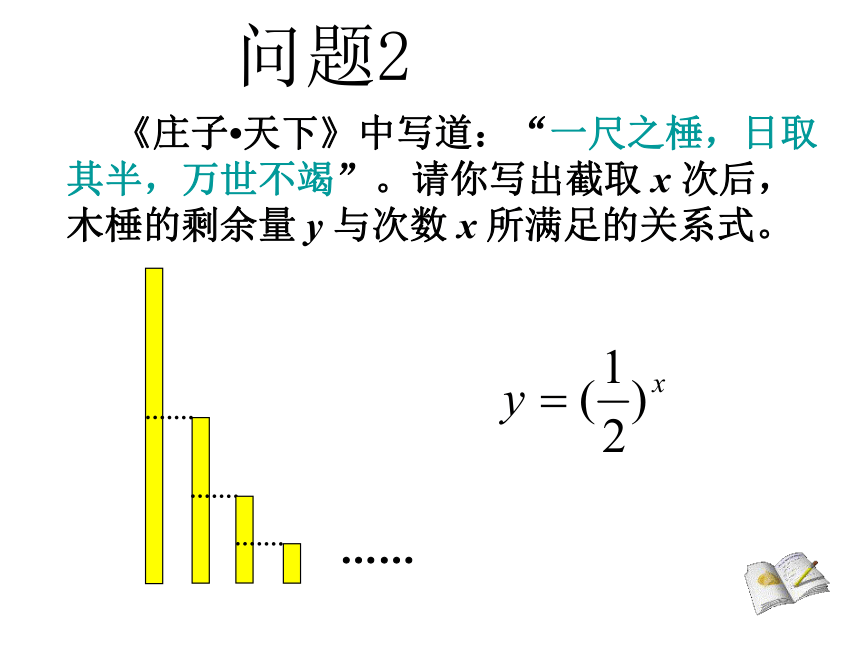
课件16张PPT。3.1.2 指数函数第3章指数函数、对数函数和幂函数问题1 把一张纸对折x次后层数y为多少？ 给我一张纸，我就可以使它的厚度超过珠穆朗玛峰！问题2 《庄子?天下》中写道：“一尺之棰，日取其半，万世不竭”。请你写出截取 x 次后，木棰的剩余量 y 与次数 x 所满足的关系式。……两个函数关系式:这两个函数有什么共同特征?学生活动y = ax1、指数函数的定义： 一般地，函数 y = ax
叫做指数函数， 建构数学(a?0，a ?1)函数的定义域是 R. 若a不满足上述条件,y=ax会怎么样?探究思路从具体的函数入手（特殊→一般）●如何研究指数函数的图象和性质？●我们一般从哪些方面去研究函数？定义、图象、性质
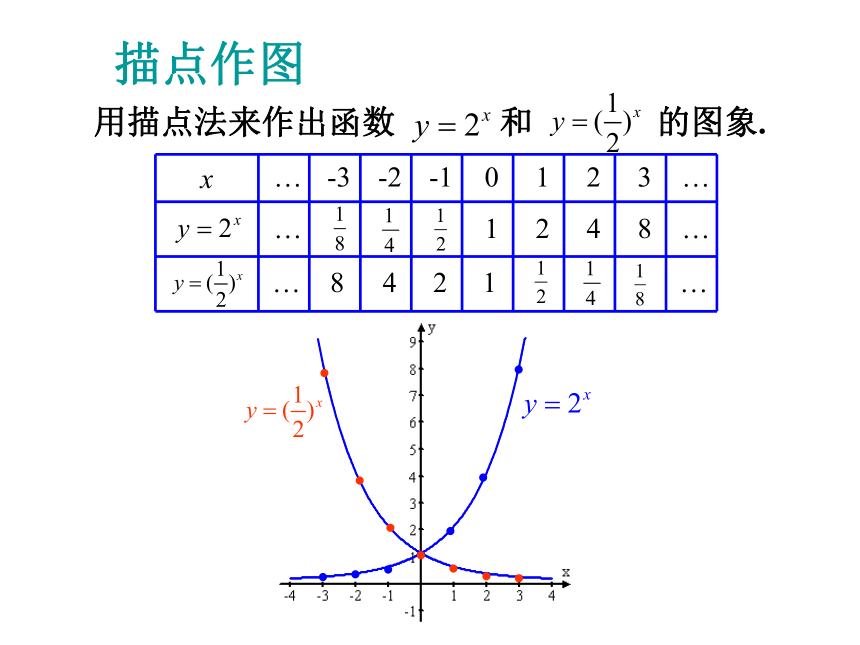
（定义域、值域、单调性、奇偶性等）作出图象?观察特征?得出性质（数形结合）●描点法作图象的基本步骤：列表、描点、连线。用描点法来作出函数和的图象. 描点作图探求图象探求图象探求图象◆当a＞1时，底数越大，图象越靠近y轴，图象上升得越快.
当0＜a＜1时，底数越小，图象越靠近y轴，图象下降得越快.（向上无限伸展，向下与x轴无限接近）● 图象特征：◆图象向左、右两方无限伸展.◆图象都在x轴上方.◆图象过定点（0，1）.◆底数互为倒数的两个指数函数图象关于y轴对称. 学生活动 ◆图象既不关于原点对称， 也不关于y轴对称. 图象与性质y=ax(1)定义域: R(2)值域：(0,+∞)(3)图象过定点:(0,1) ，即x=0 时,y=1. (4)在R上是单调增函数在R上是单调减函数(5)非奇非偶函数(7)当x>0时，y>1.
当x<0时，00时，0当x<0时，y>1.(6)函数y=ax与y=(1/a )x的图象关于y轴对称(0,1)(0,1)例1.比较下列各组数中两个值的大小：数学应用 （1）1.52.5，1.53.2（2）0.5-1.2，0.5-1.5（3）1.50.3，0.81.2（4）0.20.3，0.50.3同底数幂比较大小，构造一个指数函数，运用其单调性，转化为比较指数的大小.不同底数幂比较大小,与中间值1进行比较,构造两个指数函数，转化为同底.底数不同指数相同的两数大小比较，借助图象,数形结合.01在第一象限沿箭头方向图象对应的指数函数的底数越来越大 变式探究 底大图下
（幂小）底大图上
（幂大）在第二象限沿箭头方向图象对应的指数函数的底数越来越小0.20.3 0.50.3＜20.3 50.3＜＜0.2-0.3 0.5-0.3 2-0.3 5-0.3例2：数学应用 （1）已知3x≥30.5，求实数x的取值范围（2）已知0.2x＜25，求实数x的取值范围（3）已知ax＜ a2-x (a>0且a≠1)，求实数
x的取值范围知识的
逆用分类讨论转化为同底回顾小结: 通过本节课的学习，你对指数函数有什么认识？你有哪些收获？1、知识上：指数函数的定义、图象和性质以及应用。关键要抓住底数a>1 和0＜a＜1时函数图象的不同特征和性质。2、方法上：经历从特殊→一般→特殊的认知过程，从观察中获得知识，同时了解指数函数的实际背景和和研究函数的基本方法；体会分类讨论思想、数形结合思想。