3.1.2 指数函数 课件
图片预览






文档简介
课件20张PPT。3.1.2 指数函数第3章
指数函数、对数函数和幂函数问题情境1:折纸游戏层数y关于折叠次数x的函数为:面积y关于折叠次数x的函数为:放射性碳法测定古物年代:在动植物的体内都含
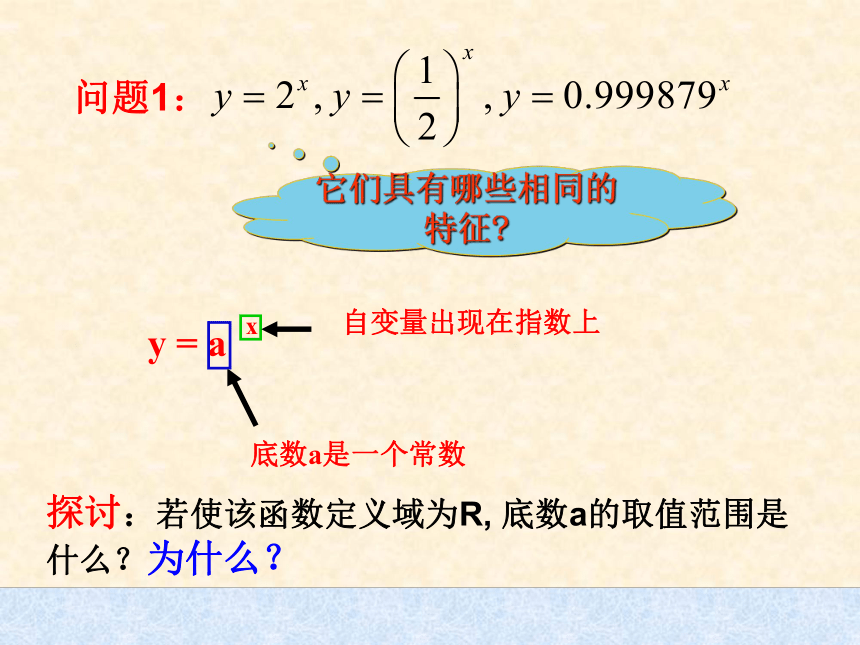
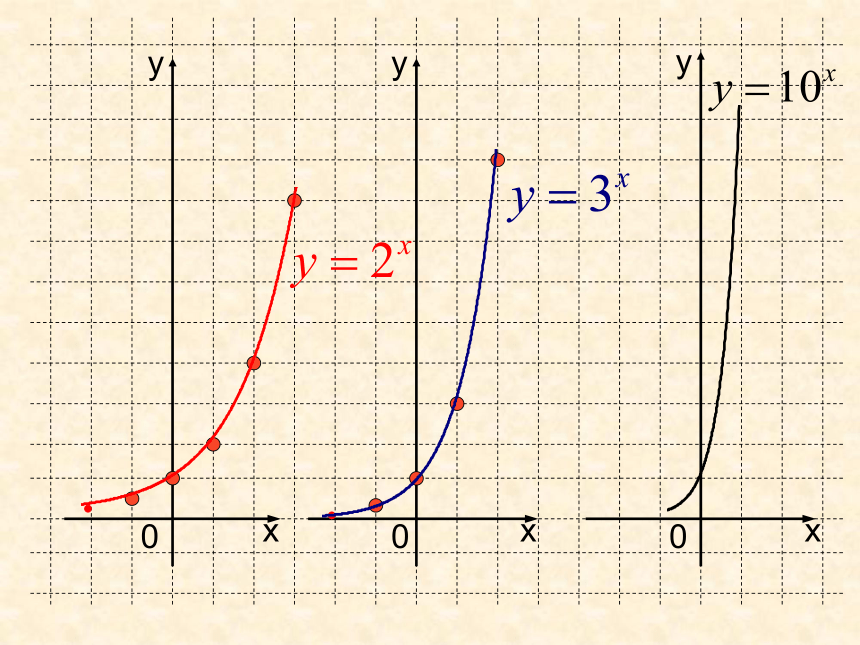
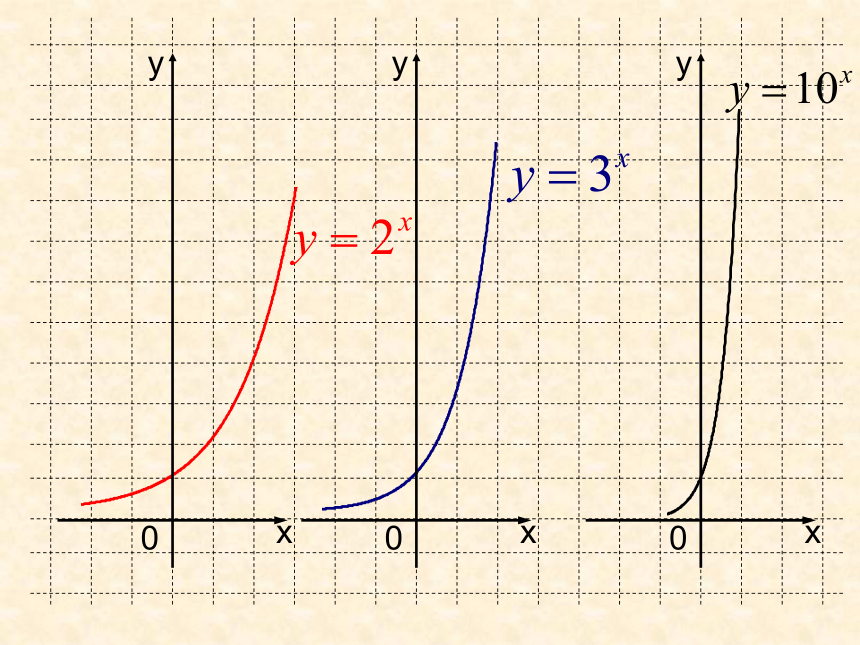
有微量的放射性14C.动植物死亡后,停止了新陈代谢,不再产生14C,且原有的14C会自动衰变.每经过一年残留量剩余为原来的0.999879倍.若14C的原始含量为1,则经过x年后14C的残留量为多少?问题情境2:残留量y关于年数x的函数关系为:问题1:它们具有哪些相同的特征?探讨:若使该函数定义域为R, 底数a的取值范围是什么?为什么?一般地,函数y=ax (a>0,a≠1) 叫做问题2:指数函数指数函数,其中x是自变量,定义域为R.您打算如何去研究指数函数?【数学建构】在不同的坐标系中画出函数 的图象. …1 2 4 …1 3 9 ……xxyy00画出函数 的图象. 问题3:在画图过程中您发现指数函数有哪些性质?R( 0 , + ∞)过定点 ( 0 , 1 )在(-∞,﹢∞)上是单调增函数(1)定义域(2)值 域 (3)定 点(4)单调性a > 10 < a < 1指数函数 的图象与性质: 在(-∞,﹢∞)上是单调减函数0101三、深入探究,加深理解 引导学生观察图象,发现图象与底的关系在第一象限沿箭头方向底增大底互为倒数的两个函数图象关于y轴对称 011011011011定义域值域奇偶性对称性单调性一般性质特殊性质值域的分布a > 10 < a < 1R( 0 , + ∞)非奇非偶非对称图形定点在R上是减函数在R上是增函数当x>0时,y>1
当x<0时,0<y<1当x>0时, 0<y<1当x<0时, y>1过定点 ( 0 , 1 ),即 x =0时,y=1图象的走势探究:指数函数性质无限接近x轴,但始终在x轴上方例1【数学运用】比较下列各组数中两个值的大小:解:考察指数函数所以 在R上是单调递增函数,又因为2.5<3.2所以【数学运用】解:有指数函数的性质知所以
指数函数、对数函数和幂函数问题情境1:折纸游戏层数y关于折叠次数x的函数为:面积y关于折叠次数x的函数为:放射性碳法测定古物年代:在动植物的体内都含
有微量的放射性14C.动植物死亡后,停止了新陈代谢,不再产生14C,且原有的14C会自动衰变.每经过一年残留量剩余为原来的0.999879倍.若14C的原始含量为1,则经过x年后14C的残留量为多少?问题情境2:残留量y关于年数x的函数关系为:问题1:它们具有哪些相同的特征?探讨:若使该函数定义域为R, 底数a的取值范围是什么?为什么?一般地,函数y=ax (a>0,a≠1) 叫做问题2:指数函数指数函数,其中x是自变量,定义域为R.您打算如何去研究指数函数?【数学建构】在不同的坐标系中画出函数 的图象. …1 2 4 …1 3 9 ……xxyy00画出函数 的图象. 问题3:在画图过程中您发现指数函数有哪些性质?R( 0 , + ∞)过定点 ( 0 , 1 )在(-∞,﹢∞)上是单调增函数(1)定义域(2)值 域 (3)定 点(4)单调性a > 10 < a < 1指数函数 的图象与性质: 在(-∞,﹢∞)上是单调减函数0101三、深入探究,加深理解 引导学生观察图象,发现图象与底的关系在第一象限沿箭头方向底增大底互为倒数的两个函数图象关于y轴对称 011011011011定义域值域奇偶性对称性单调性一般性质特殊性质值域的分布a > 10 < a < 1R( 0 , + ∞)非奇非偶非对称图形定点在R上是减函数在R上是增函数当x>0时,y>1
当x<0时,0<y<1当x>0时, 0<y<1当x<0时, y>1过定点 ( 0 , 1 ),即 x =0时,y=1图象的走势探究:指数函数性质无限接近x轴,但始终在x轴上方例1【数学运用】比较下列各组数中两个值的大小:解:考察指数函数所以 在R上是单调递增函数,又因为2.5<3.2所以【数学运用】解:有指数函数的性质知所以
