3.2.1 对数——对数的运算性质 课件
图片预览








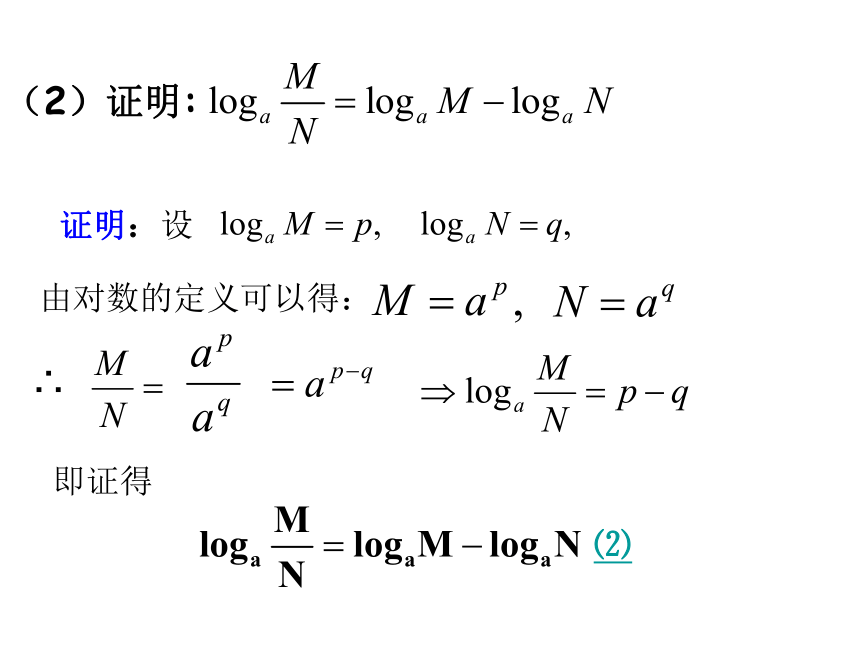
文档简介
课件23张PPT。3.2.1 对数---对数的运算性质一般地,如果 的b次幂等于N, 就是 ,那么数 b叫做以a为底 N的对数,记作 a 叫做对数的底数,N叫做真数.1.对数概念:复习2.指数式与对数式互化⑴负数与零没有对数(∵在指数式中 N > 0 ) ⑶对数恒等式3.重要结论:⑵基本性质⑷常用对数: ⑸自然对数: 练习 计算下列各式:43?(1)(2)(3)指数幂运算有下列性质根据对数的定义,有(a > 0,a ? 1, N > 0) 对数运算也有相应的性质吗?课中研学:对数的运算性质两个正数的积的对数等于这两个正数的对数和两个正数的商的对数等于这两个正数的对数差语言表达:一个正数的n次方的对数等于这个正数的对数n倍如果 a > 0,a ? 1,M > 0, N > 0 有:证明:①设 由对数的定义可以得: ∴MN= 即证得 (1)证明:⑴证明:设 由对数的定义可以得: ∴ 即证得 (2)证明:证明:设 由对数的定义可以得: ∴即证得 (3)证明:⑶课堂小结:对数的运算性质如果 a > 0,a ? 1,M > 0, N > 0 有:其他重要公式1:证明:设 即证得 其他重要公式2:这个公式叫做换底公式其他重要公式3:对数的 换 底 公 式换底公式不难记,
一数等于两数比;
相对位置不改变,
新的底数可随意.(非1正数)课中研学:公 式 应 用:推论:证明:设 即证得 例8.2000年我国国内生产总值(GDP)为89442亿元.如果我国 GDP年均增长7.8%左右,按照这个增长速度,在2000年的基础上,经过多少年以后,我国的GDP才能实现比2000年翻两番的目标?解:假设经过x年实现GDP比2000年翻两番的目标,根据题意,得 89442×(1+7.8%)x=89442×4
即 1.078x=4
∴x=log1.0784
=lg4/lg1.078
≈18.5 (年)
答:约经过19年以后,我国的GDP才能实现比2000年翻两番的目标。
例9.(古莲子问题)我国辽东半岛普兰店附近的泥炭中发掘出的古莲子至今大部分还能发芽开花. 现已测得出土的古莲子中的14C的残余量占原来的87.9%,试推算古莲子的生活年代. 在动植物体内都含有微量的放射性14C,动植物死后,原有的14C会自动衰变,经过5730年,它的残余量只有原始量的一半,经过科学测定,若14C的原始含量为1,则x年后的残余量为y=0.999879x
分析:设古莲子是x年前的植物.0.879=0.999879x ?x=log0.9998790.879所以古莲子约是1066年前的遗物.例10.已知 log 2 3 = a,log 3 7 = b,用 a, b 表示log 42 56
由已知得:log23×log37=log27=ab练习:已知log95=m,log37=n,用m,n表示log359.解:∵log935=log9(5×7)=log95+log97又log95=m,
一数等于两数比;
相对位置不改变,
新的底数可随意.(非1正数)课中研学:公 式 应 用:推论:证明:设 即证得 例8.2000年我国国内生产总值(GDP)为89442亿元.如果我国 GDP年均增长7.8%左右,按照这个增长速度,在2000年的基础上,经过多少年以后,我国的GDP才能实现比2000年翻两番的目标?解:假设经过x年实现GDP比2000年翻两番的目标,根据题意,得 89442×(1+7.8%)x=89442×4
即 1.078x=4
∴x=log1.0784
=lg4/lg1.078
≈18.5 (年)
答:约经过19年以后,我国的GDP才能实现比2000年翻两番的目标。
例9.(古莲子问题)我国辽东半岛普兰店附近的泥炭中发掘出的古莲子至今大部分还能发芽开花. 现已测得出土的古莲子中的14C的残余量占原来的87.9%,试推算古莲子的生活年代. 在动植物体内都含有微量的放射性14C,动植物死后,原有的14C会自动衰变,经过5730年,它的残余量只有原始量的一半,经过科学测定,若14C的原始含量为1,则x年后的残余量为y=0.999879x
分析:设古莲子是x年前的植物.0.879=0.999879x ?x=log0.9998790.879所以古莲子约是1066年前的遗物.例10.已知 log 2 3 = a,log 3 7 = b,用 a, b 表示log 42 56
由已知得:log23×log37=log27=ab练习:已知log95=m,log37=n,用m,n表示log359.解:∵log935=log9(5×7)=log95+log97又log95=m,
