人教版八年级数学下册 课件: 17.2 勾股定理的逆定理(共30张PPT)
文档属性
| 名称 | 人教版八年级数学下册 课件: 17.2 勾股定理的逆定理(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-06 00:00:00 | ||
图片预览






文档简介
课件30张PPT。勾股定理的逆定理(1)回忆1. 直角三角形有哪些性质?(1)有一个角是直角;
(2)两个锐角互余;
(3)两直角边的平方和等于斜边的平方;
(4)在含30°角的直角三角形中,30°
的角所对的直角边是斜边的一半2. 一个三角形,满足什么条件是直角三角形?有一个内角是90°,那么这个三角形就为直角三角形。如果一个三角形中,有两个角的和是90°,那么这
个三角形也是直角三角形。我们是否可以不用角,而用三角形三边的关系
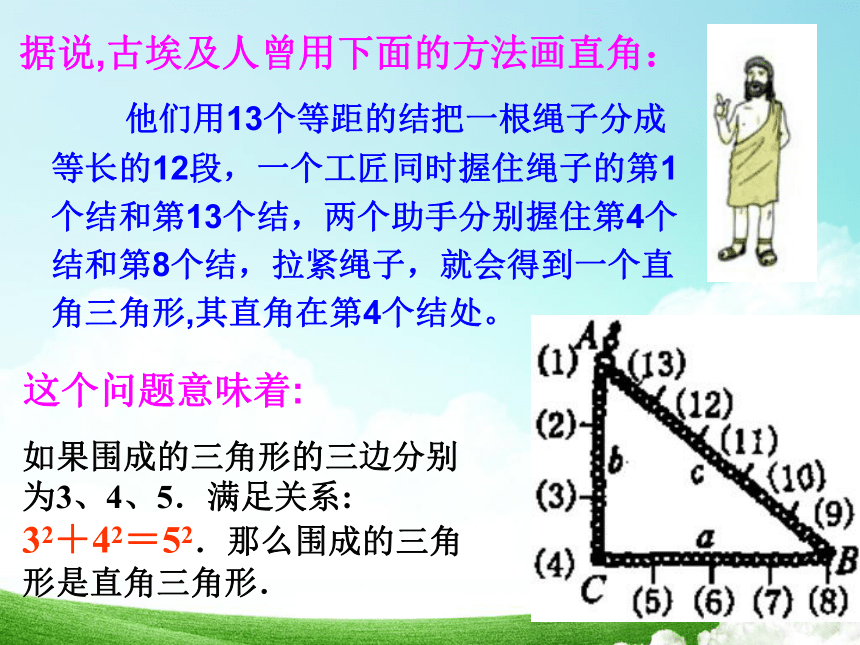
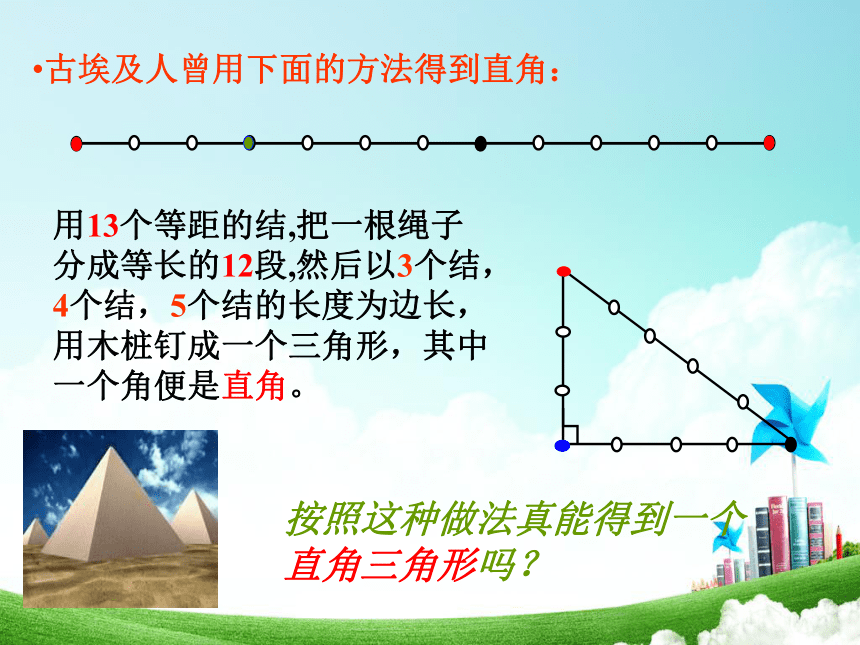
来判断是否为直角三角形呢?古埃及人曾用下面的方法得到直角据说,古埃及人曾用下面的方法画直角:
他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处。这个问题意味着:如果围成的三角形的三边分别为3、4、5.满足关系: 32+42=52.那么围成的三角形是直角三角形.按照这种做法真能得到一个直角三角形吗? 古埃及人曾用下面的方法得到直角:用13个等距的结,把一根绳子分成等长的12段,然后以3个结,4个结,5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角。
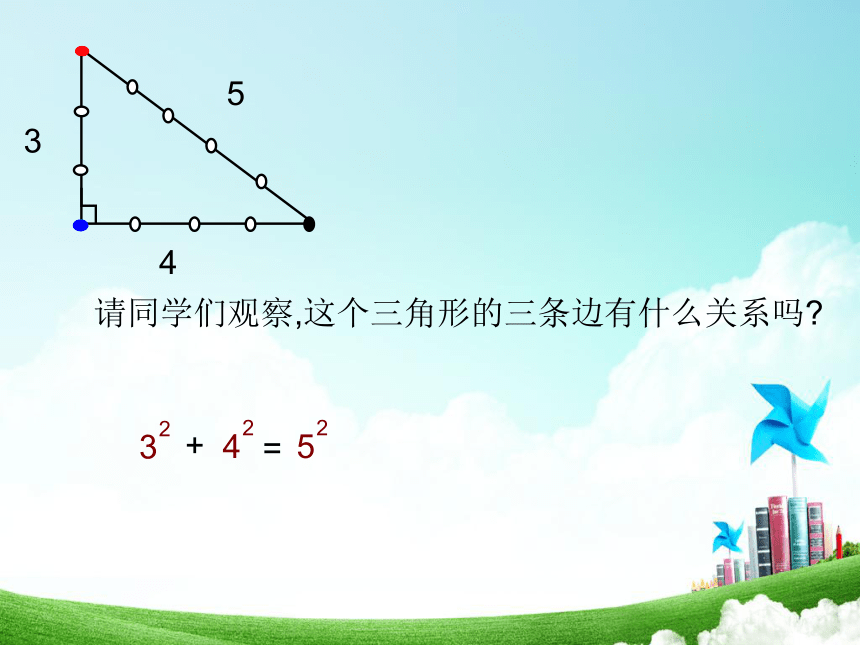
345请同学们观察,这个三角形的三条边有什么关系吗? 下面的三组数分别是一个三角形的三边长a,b,c:2.5,6,6.5; 6,8,10。动手画一画由上面几个例子你发现了什么吗?请以命题的
形式说出你的观点!命题2如果直角三角形的两直角边长分别为a、
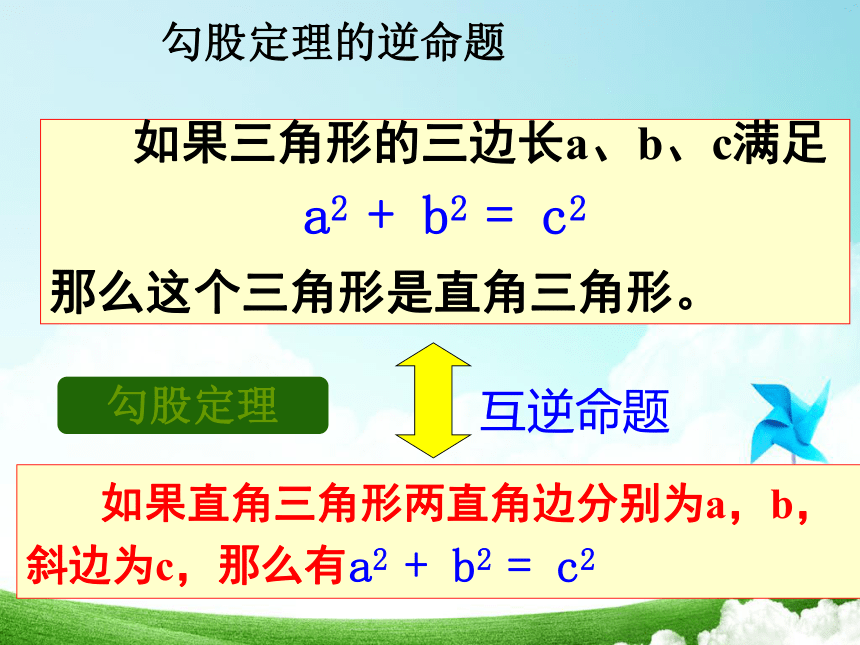
b,斜边长c,那么a2+b2=c2 命题1:如果三角形的三边长a,b,c有关系a2+b2=c2,
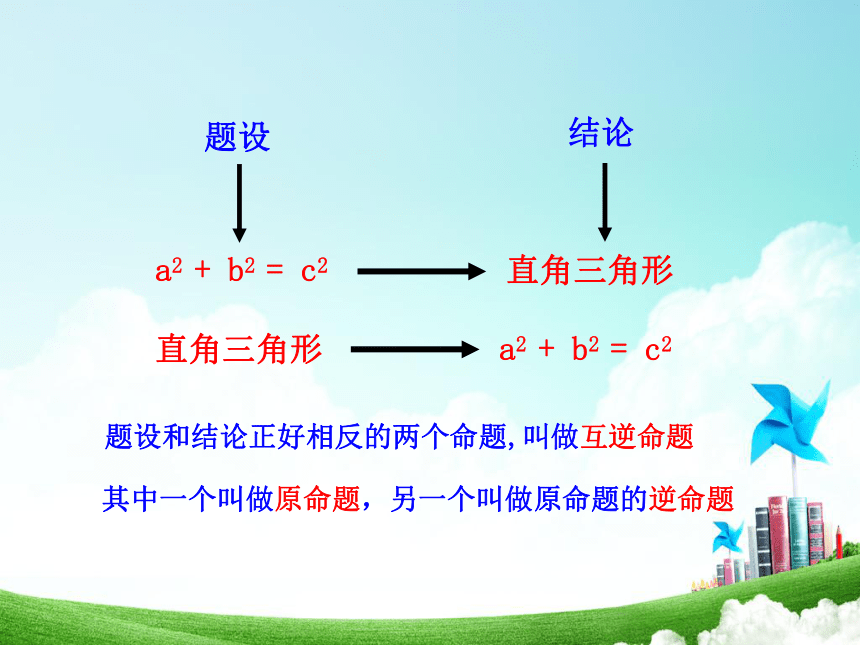
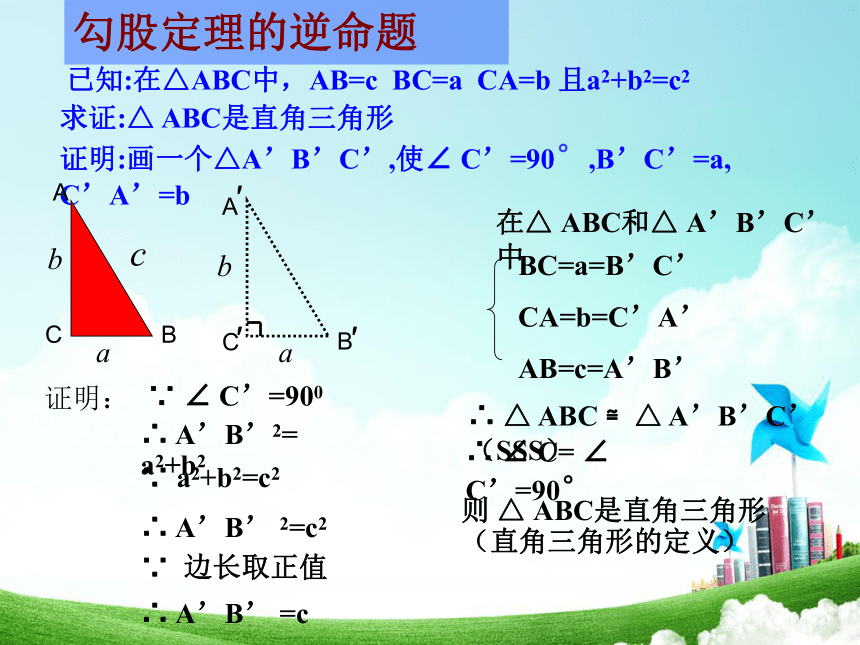
那么这个三角形是直角三角形.命题2:对在这两个命题中, 题设和结论正好相反,我们把这样的两个命题叫做互逆命题,如果把其中一个命题叫做原命题,那么另一个叫做它的逆命题. 办 温顾而知新观察上面两个命题,它们的题设与结论之间有怎样的关系?与同伴交流.活动五:a2 + b2 = c2题设结论直角三角形直角三角形a2 + b2 = c2题设和结论正好相反的两个命题,叫做互逆命题其中一个叫做原命题,另一个叫做原命题的逆命题 勾股定理的逆命题勾股定理互逆命题∵ ∠ C’=900∴ A’B’2= a2+b2∵ a2+b2=c2∴ A’B’ 2=c2∴ A’B’ =c∵ 边长取正值∴ △ ABC ≌△ A’B’C’(SSS)∴ ∠ C= ∠ C’=90°已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2求证:△ ABC是直角三角形证明:画一个△A’B’C’,使∠ C’=90°,B’C’=a, C’A’=b在△ ABC和△ A’B’C’中则 △ ABC是直角三角形(直角三角形的定义)勾股定理的逆命题ACB证明:勾股定理的逆命题勾股定理互逆命题逆定理定理驶向胜利的彼岸定理与逆定理我们已经学习了一些互逆的定理,如:
勾股定理及其逆定理;
两直线平行,内错角相等;内错角相等,两直线平行.如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.(1)两条直线平行,内错角相等.
(2)如果两个实数相等,那么它们的平方相等.
(3)如果两个实数相等,那么它们的绝对值相等.
(4)全等三角形的对应角相等.说出下列命题的逆命题.这些命题的逆命题成立吗?逆命题: 内错角相等,两条直线平行. 成立逆命题:如果两个实数的平方相等,那么这两个实数相等. 不成立逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 不成立逆命题:对应角相等的两个三角形是全等三角形. 不成立感悟: 原命题成立时, 逆命题有时成立, 有时不成立一个命题是真命题,它逆命题却不一定是真命题.例1 判断由a、b、c组成的三角形是不是直角三角形:
(1) a=15 , b =8 , c=17(2) a=13 , b =15 , c=14分析:由勾股定理的逆定理,判断三角形是不是直角三角形,只要看两条较小边的平方和是否等于最大边的平方。解:∵152+82=225+64=289
172=289
∴ 152+82=172
∴这个三角形是直角三角形 分析:根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较少边长的平方和是否等于最大边长的平方. 例1:判断由线段a,b,c组成的三角形是不是直角
三角形?
(1) a=15,b=17,c=8; (2) a=13,b=15,c=14 解:(1)最大边为17 ∵152+82=225+64 =289172 =289 ∴152+82 =172 ∴以15, 8, 17为边长的三角形是直角三角形 (2)最大边为15 ∵132+142=169+196=365152 =225 ∴132+ 142 ≠ 152 ∴以13, 15, 14为边长的三角形不是直角三角形 像15,17,8,能够成为直角三角形三条边长的三个正整数,称为勾股数. 例 2.在△ABC中,a=15, b=17, c=8,求此三角形的面积。∴△ABC为直角三角形,且∠B=90°
∴ △ABC的面积为81517ABC 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900(3) a=1 b=2 c= ____ _____ ; 像25,20,15,能够成为直角三角形三条边长的三个正整数,称为勾股数.例4: “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
BA、锐角三角形 B、直角三角形C、钝角三角形 D、等边三角形1.
已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积?
S四边形ABCD=36分析:先来判断a,b,c三边哪条最长,可以代m,n为满足条件的特殊值来试,m=5,n=4.则a=9,b=40,c=41,c最大。∴△ABC是直角三角形1、请你写出三组勾股数;
2、一组勾股数的倍数一定是勾股数吗?为什么?1、 已知a,b,c为△ABC的三边,且 满足
a2+b2+c2+338=10a+24b+26c.
试判断△ABC的形状.2、△ABC三边a,b,c为边向外作正方形,正三角形,以三边为直径作半圆,若S1+S2=S3成立,则是直角三角形吗?
ACabcS1S2S3BABCabcS1S2S3……请谈谈你的收获自主评价:1、勾股定理的逆定理2、什么叫做互逆命题、原命题与逆命题3、什么称为互为逆定理。回味无穷勾股定理:
如果直角三角形两直角边分别为a、b,斜边为c,那么a2+b2=c2.即直角三角形两直角边的平方和等于斜边的平方.勾股定理在西方文献中又称为毕达哥拉斯定理(pythagoras theorem).
勾股定理的逆定理:
如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.
命题与逆命题
在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.
定理与逆定理
如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.
(2)两个锐角互余;
(3)两直角边的平方和等于斜边的平方;
(4)在含30°角的直角三角形中,30°
的角所对的直角边是斜边的一半2. 一个三角形,满足什么条件是直角三角形?有一个内角是90°,那么这个三角形就为直角三角形。如果一个三角形中,有两个角的和是90°,那么这
个三角形也是直角三角形。我们是否可以不用角,而用三角形三边的关系
来判断是否为直角三角形呢?古埃及人曾用下面的方法得到直角据说,古埃及人曾用下面的方法画直角:
他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在第4个结处。这个问题意味着:如果围成的三角形的三边分别为3、4、5.满足关系: 32+42=52.那么围成的三角形是直角三角形.按照这种做法真能得到一个直角三角形吗? 古埃及人曾用下面的方法得到直角:用13个等距的结,把一根绳子分成等长的12段,然后以3个结,4个结,5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角。
345请同学们观察,这个三角形的三条边有什么关系吗? 下面的三组数分别是一个三角形的三边长a,b,c:2.5,6,6.5; 6,8,10。动手画一画由上面几个例子你发现了什么吗?请以命题的
形式说出你的观点!命题2如果直角三角形的两直角边长分别为a、
b,斜边长c,那么a2+b2=c2 命题1:如果三角形的三边长a,b,c有关系a2+b2=c2,
那么这个三角形是直角三角形.命题2:对在这两个命题中, 题设和结论正好相反,我们把这样的两个命题叫做互逆命题,如果把其中一个命题叫做原命题,那么另一个叫做它的逆命题. 办 温顾而知新观察上面两个命题,它们的题设与结论之间有怎样的关系?与同伴交流.活动五:a2 + b2 = c2题设结论直角三角形直角三角形a2 + b2 = c2题设和结论正好相反的两个命题,叫做互逆命题其中一个叫做原命题,另一个叫做原命题的逆命题 勾股定理的逆命题勾股定理互逆命题∵ ∠ C’=900∴ A’B’2= a2+b2∵ a2+b2=c2∴ A’B’ 2=c2∴ A’B’ =c∵ 边长取正值∴ △ ABC ≌△ A’B’C’(SSS)∴ ∠ C= ∠ C’=90°已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2求证:△ ABC是直角三角形证明:画一个△A’B’C’,使∠ C’=90°,B’C’=a, C’A’=b在△ ABC和△ A’B’C’中则 △ ABC是直角三角形(直角三角形的定义)勾股定理的逆命题ACB证明:勾股定理的逆命题勾股定理互逆命题逆定理定理驶向胜利的彼岸定理与逆定理我们已经学习了一些互逆的定理,如:
勾股定理及其逆定理;
两直线平行,内错角相等;内错角相等,两直线平行.如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.(1)两条直线平行,内错角相等.
(2)如果两个实数相等,那么它们的平方相等.
(3)如果两个实数相等,那么它们的绝对值相等.
(4)全等三角形的对应角相等.说出下列命题的逆命题.这些命题的逆命题成立吗?逆命题: 内错角相等,两条直线平行. 成立逆命题:如果两个实数的平方相等,那么这两个实数相等. 不成立逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 不成立逆命题:对应角相等的两个三角形是全等三角形. 不成立感悟: 原命题成立时, 逆命题有时成立, 有时不成立一个命题是真命题,它逆命题却不一定是真命题.例1 判断由a、b、c组成的三角形是不是直角三角形:
(1) a=15 , b =8 , c=17(2) a=13 , b =15 , c=14分析:由勾股定理的逆定理,判断三角形是不是直角三角形,只要看两条较小边的平方和是否等于最大边的平方。解:∵152+82=225+64=289
172=289
∴ 152+82=172
∴这个三角形是直角三角形 分析:根据勾股定理的逆定理, 判断一个三角形是不是直角三角形, 只要看两条较少边长的平方和是否等于最大边长的平方. 例1:判断由线段a,b,c组成的三角形是不是直角
三角形?
(1) a=15,b=17,c=8; (2) a=13,b=15,c=14 解:(1)最大边为17 ∵152+82=225+64 =289172 =289 ∴152+82 =172 ∴以15, 8, 17为边长的三角形是直角三角形 (2)最大边为15 ∵132+142=169+196=365152 =225 ∴132+ 142 ≠ 152 ∴以13, 15, 14为边长的三角形不是直角三角形 像15,17,8,能够成为直角三角形三条边长的三个正整数,称为勾股数. 例 2.在△ABC中,a=15, b=17, c=8,求此三角形的面积。∴△ABC为直角三角形,且∠B=90°
∴ △ABC的面积为81517ABC 下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ____ _____ ;(2) a=13 b=14 c=15 ____ _____ ;(4) a:b: c=3:4:5 _____ _____ ;是是不是 是∠ A=900∠ B=900∠ C=900(3) a=1 b=2 c= ____ _____ ; 像25,20,15,能够成为直角三角形三条边长的三个正整数,称为勾股数.例4: “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
BA、锐角三角形 B、直角三角形C、钝角三角形 D、等边三角形1.
已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积?
S四边形ABCD=36分析:先来判断a,b,c三边哪条最长,可以代m,n为满足条件的特殊值来试,m=5,n=4.则a=9,b=40,c=41,c最大。∴△ABC是直角三角形1、请你写出三组勾股数;
2、一组勾股数的倍数一定是勾股数吗?为什么?1、 已知a,b,c为△ABC的三边,且 满足
a2+b2+c2+338=10a+24b+26c.
试判断△ABC的形状.2、△ABC三边a,b,c为边向外作正方形,正三角形,以三边为直径作半圆,若S1+S2=S3成立,则是直角三角形吗?
ACabcS1S2S3BABCabcS1S2S3……请谈谈你的收获自主评价:1、勾股定理的逆定理2、什么叫做互逆命题、原命题与逆命题3、什么称为互为逆定理。回味无穷勾股定理:
如果直角三角形两直角边分别为a、b,斜边为c,那么a2+b2=c2.即直角三角形两直角边的平方和等于斜边的平方.勾股定理在西方文献中又称为毕达哥拉斯定理(pythagoras theorem).
勾股定理的逆定理:
如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.
命题与逆命题
在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.
定理与逆定理
如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.
