2024-2025学年山西省人教版六年级下册小升初备考真题分类汇编专题05图形计算数学试卷(含解析)
文档属性
| 名称 | 2024-2025学年山西省人教版六年级下册小升初备考真题分类汇编专题05图形计算数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 545.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-06 16:40:00 | ||
图片预览

文档简介
专题04 图形计算-2024-2025学年
小升初数学备考真题分类汇编(山西地区专版)
一、平面图形
(一)组合图形周长及面积计算
(2023·山西长治·小升初真题)
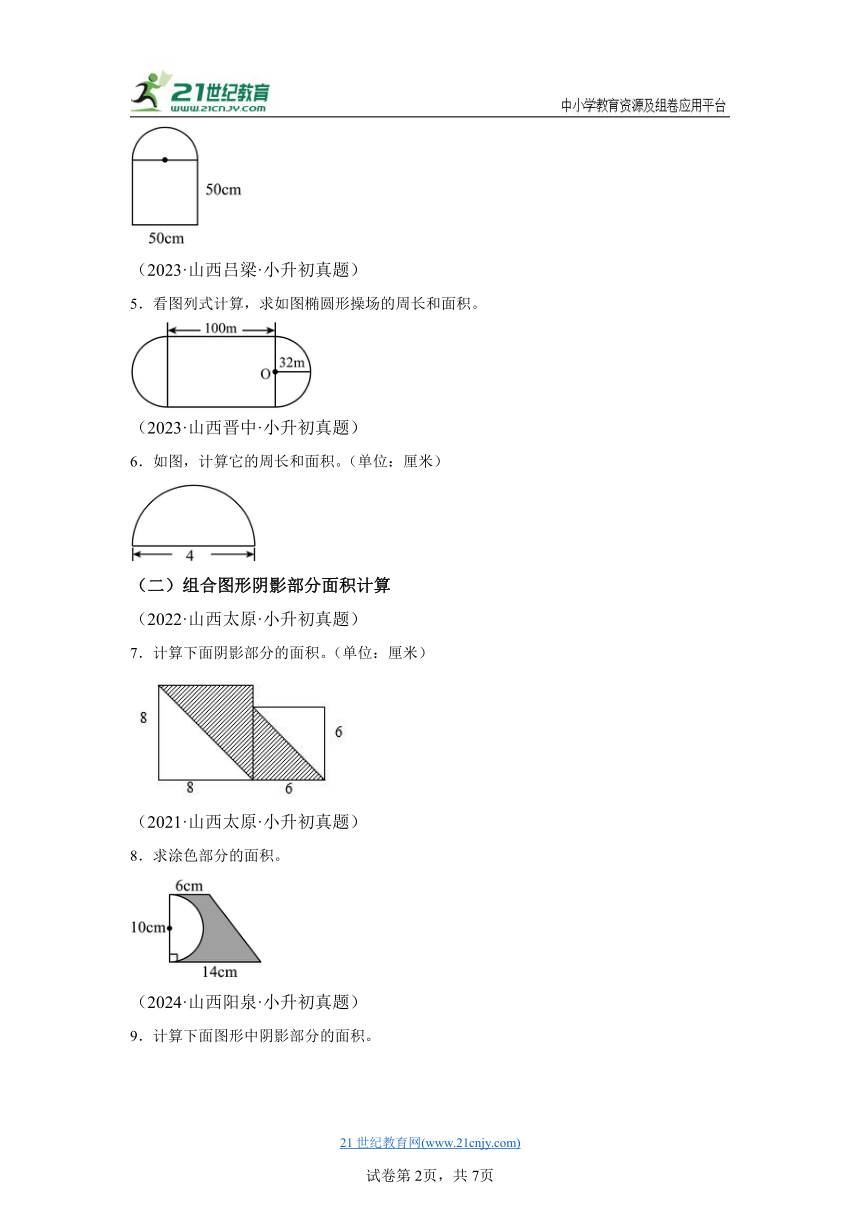
1.求下面梯形和半圆的面积(单位:厘米)。
(2024·山西长治·小升初真题)
2.计算下面图形的面积。(单位:cm)
(2024·山西太原·小升初真题)
3.求出下面两图形的周长。(单位:厘米)
(2024·山西大同·小升初真题)
4.求图的周长。
(2023·山西吕梁·小升初真题)
5.看图列式计算,求如图椭圆形操场的周长和面积。
(2023·山西晋中·小升初真题)
6.如图,计算它的周长和面积。(单位:厘米)
(二)组合图形阴影部分面积计算
(2022·山西太原·小升初真题)
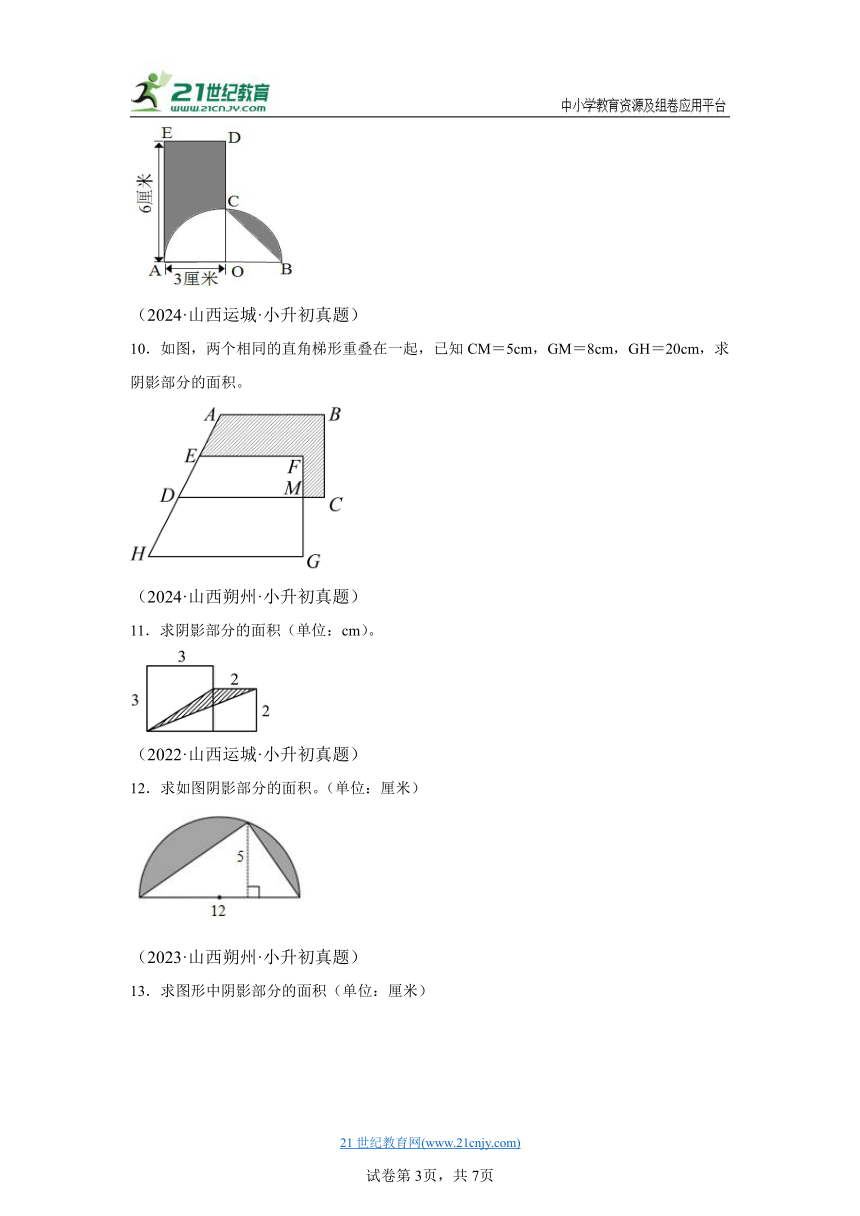
7.计算下面阴影部分的面积。(单位:厘米)
(2021·山西太原·小升初真题)
8.求涂色部分的面积。
(2024·山西阳泉·小升初真题)
9.计算下面图形中阴影部分的面积。
(2024·山西运城·小升初真题)
10.如图,两个相同的直角梯形重叠在一起,已知CM=5cm,GM=8cm,GH=20cm,求阴影部分的面积。
(2024·山西朔州·小升初真题)
11.求阴影部分的面积(单位:cm)。
(2022·山西运城·小升初真题)
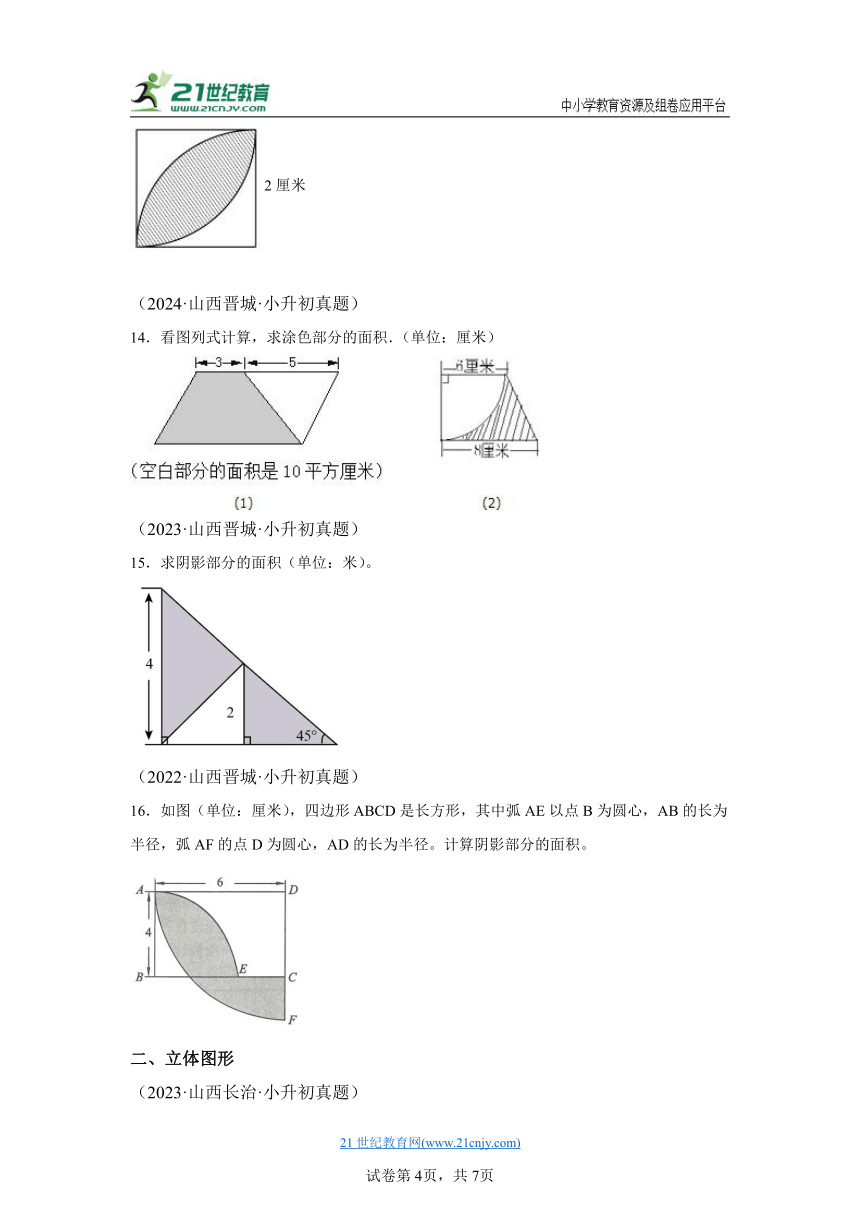
12.求如图阴影部分的面积。(单位:厘米)
(2023·山西朔州·小升初真题)
13.求图形中阴影部分的面积(单位:厘米)
2厘米
(2024·山西晋城·小升初真题)
14.看图列式计算,求涂色部分的面积.(单位:厘米)
(2023·山西晋城·小升初真题)
15.求阴影部分的面积(单位:米)。
(2022·山西晋城·小升初真题)
16.如图(单位:厘米),四边形ABCD是长方形,其中弧AE以点B为圆心,AB的长为半径,弧AF的点D为圆心,AD的长为半径。计算阴影部分的面积。
二、立体图形
(2023·山西长治·小升初真题)
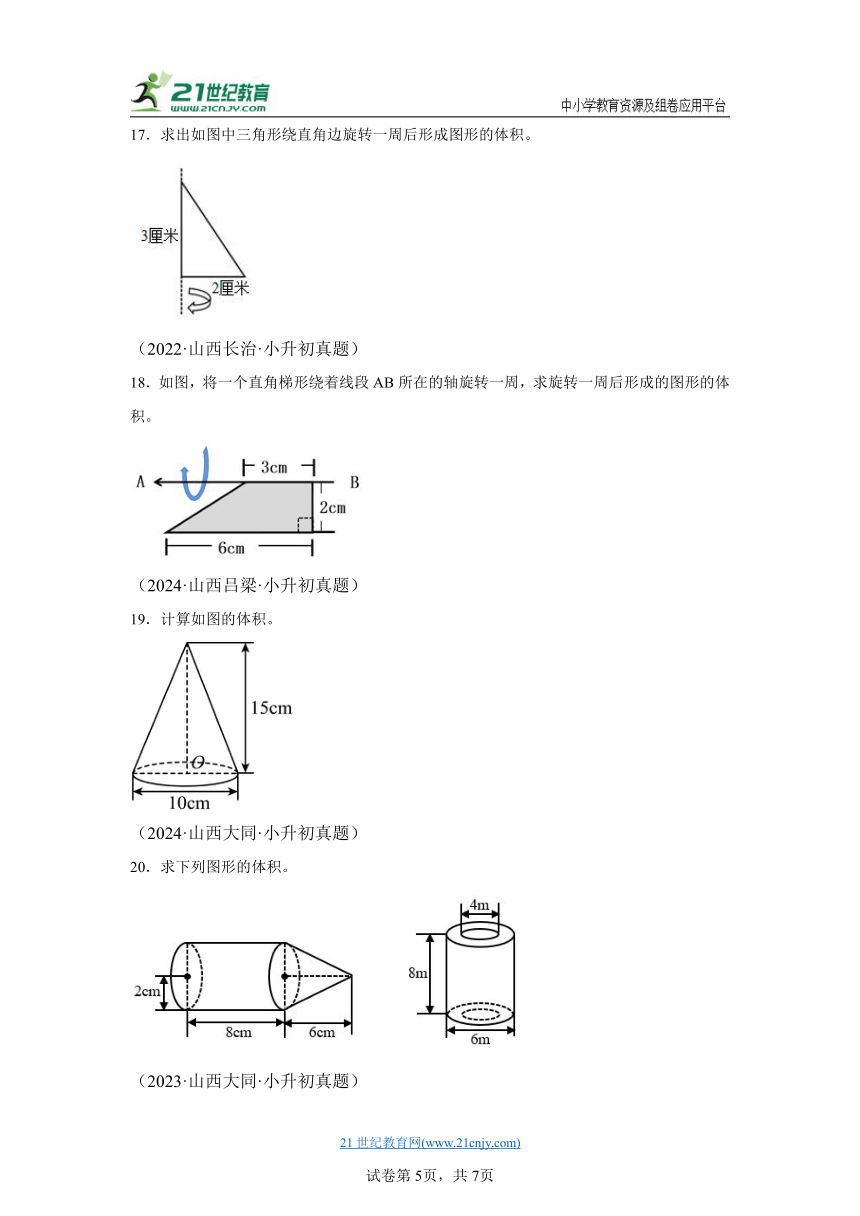
17.求出如图中三角形绕直角边旋转一周后形成图形的体积。
(2022·山西长治·小升初真题)
18.如图,将一个直角梯形绕着线段AB所在的轴旋转一周,求旋转一周后形成的图形的体积。
(2024·山西吕梁·小升初真题)
19.计算如图的体积。
(2024·山西大同·小升初真题)
20.求下列图形的体积。
(2023·山西大同·小升初真题)
21.一个零件的形状如下图所示,求这个零件的体积。
(2024·山西·小升初真题)
22.求下面立体图形的体积(单位:分米)
(2023·山西临汾·小升初真题)
23.如图是圆柱体的表面展开图,请计算出这个圆柱的表面积。
(2024·山西忻州·小升初真题)
24.计算下图的体积。(单位:cm)
(2023·山西忻州·小升初真题)
25.计算下面图形的表面积。
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
试卷第1页,共3页
《2024-2025学年山西省人教版六年级下册小升初备考真题分类汇编专题05 图形计算数学试卷》参考答案:
1.7平方厘米;25.12平方厘米
【详解】梯形的面积:
×2×(2+5)
=×2×7
=7(平方厘米)
圆的面积:
×3.14×()2
=×3.14×16
=25.12(平方厘米)
2.15.6
【详解】3.2×3.5÷2
=11.2÷2
=5.6()
(3.2+4.8)×2.5÷2
=8×2.5÷2
=10()
5.6+10=15.6()
3.37.68厘米;35.7厘米
【分析】根据圆的周长=πd,代入数据即可解答;
图形的周长=πr+4r,代入数据即可解答。
【详解】3.14×12=37.68(厘米)
3.14×5+5×4
=15.7+20
=35.7(厘米)
4.228.5厘米
【分析】观察图形可知,这个图形的周长等于3条50厘米的线段之和,再加上直径50厘米的圆的周长的一半,据此利用圆的周长公式计算即可解答。
【详解】50×3+3.14×50÷2
=150+78.5
=228.5(厘米)
图的周长是228.5厘米。
5.周长是400.96m,面积是9615.36m2
【分析】(1)椭圆形操场的周长等于两个圆弧的长加上长方形的两条长,即半径是32米的圆的周长加上长方形的两条长。
(2)椭圆形操场的面积等于长方形的面积加上两个半圆,即长方形的面积加上半径是32米的圆的面积。
【详解】(1)椭圆形操场的周长为:
2×3.14×32+100×2
=200.96+200
=400.96(m)
(2)椭圆形操场的面积为:
3.14×322+100×(32×2)
=3.14×1024+100×64
=3215.36+6400
=9615.36(m2)
椭圆形操场的周长是400.96m,面积是9615.36m2。
【点睛】此题主要考查了组合图形的周长和面积的求法,解答此题的关键是熟练掌握长方形、圆的周长和面积公式。
6.图形的周长是10.28厘米,面积是6.28平方厘米
【分析】图形的周长等于圆的周长的一半再加上一条直径的长度,直径的长度已知,从而问题得解。半圆的面积等于圆的面积的一半,利用圆的面积公式即可得解。
【详解】周长:3.14×4÷2+4
=12.56÷2+4
=6.28+4
=10.28(厘米)
面积:3.14×(4÷2)2÷2
=3.14×4÷2
=12.56÷2
=6.28(平方厘米)
图形的周长是10.28厘米,面积是6.28平方厘米。
【点睛】此题主要考查圆的周长和面积的计算方法,关键是计算周长时别忘了加直径。
7.50
【详解】8×8÷2+6×6÷2
=32+18
=50()
答:阴影部分的面积是50。
8.60.75cm2
【分析】涂色部分的面积=梯形面积-半圆的面积,根据梯形面积=(上底+下底)×高÷2,圆的面积公式:S=πr2,代入数据求解即可。
【详解】(6+14)×10÷2-3.14×(10÷2)2÷2
=100-39.25
=60.75(cm2)
9.13.5平方厘米
【分析】如下图,把右边的阴影部分移补到如箭头所示的左边空白部分,这样阴影部分合并成一个梯形,梯形的上底是(6-3)厘米,下底是6厘米,高是3厘米,根据梯形的面积=(上底+下底)×高÷2,代入数据计算求出阴影部分的面积。
【详解】(6-3+6)×3÷2
=9×3÷2
=13.5(平方厘米)
阴影部分的面积是13.5平方厘米。
10.140平方厘米
【分析】通过观察图形可知,阴影部分的面积=S梯形ABCD-S梯形EFMD,S梯形DMGH=S梯形EFGH-S梯形EFMD,S梯形ABCD和S梯形EFGH是两个相同的直角梯形,故阴影部分的面积和梯形DMGH的面积相等,阴影部分转化为梯形DMGH的面积,根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【详解】根据分析可得:
S阴影部分的面积=S梯形DMGH
(平方厘米)
因此,阴影部分的面积是140平方厘米。
11.2cm2
【分析】观察图形可知,阴影部分是一个底为2cm、高为2cm的三角形,根据三角形的面积=底×高÷2,代入数据计算求出阴影部分的面积。
【详解】2×2÷2=2(cm2)
阴影部分的面积是2cm2。
12.26.52平方厘米
【分析】由图可知:阴影部分的面积=半圆的面积-三角形的面积,代入数据计算即可。
【详解】
=3.14×36÷2
=113.04÷2
=56.52(平方厘米)
=60÷2
=30(平方厘米)
56.52-30=26.52(平方厘米)
13.2.28平方厘米
【分析】通过切拼(如下图),即可得阴影部分的面积=半圆的面积-三角形的面积,已知半圆的半径是2厘米,三角形的底是2+2=4(厘米),高是2厘米,根据半圆的面积:S=π22÷2,三角形的面积=底×高÷2,分别代入数据计算,再相减即可。
【详解】
2厘米
22×3.14÷2-4×2÷2
=4×3.14÷2-4×2÷2
=12.56÷2-4×2÷2
=6.28-4×2÷2
=6.28-8÷2
=6.28-4
=2.28(平方厘米)
阴影部分的面积是2.28平方厘米。
14.(1)22平方厘米.
(2)13.74平方厘米
【分析】(1)阴影部分是梯形,根据空白部分的面积和底,可求出空白部分的高,也就是梯形的高,代入梯形的面积公式即可求出阴影部分的面积.(2)梯形的面积减去四分之一圆的面积就是阴影部分的面积,梯形的上底和高等于四分之一圆的半径,下底是8厘米,代入公式计算即可.
【详解】(1)10×2÷5=4(厘米)
(3+3+5)×4÷2
=11×4÷2
=22(平方厘米)
答:涂色部分的面积是22平方厘米.
(2)(6+8)×6÷2﹣3.14×62÷4
=14×6÷2﹣28.26
=42﹣28.26
=13.74(平方厘米)
答:涂色部分的面积是13.74平方厘米
15.6平方米
【分析】根据等腰三角形的特征,等腰三角形的两条腰的长度相等,再根据三角形的面积公式:S=ah÷2,阴影部分的面积等于大三角形的面积与小三角形的面积差,把数据代入公式解答。
【详解】4×4÷2﹣2×2÷2
=8﹣2
=6(平方米)
答:阴影部分的面积是6平方米。
16.16.82平方厘米
【分析】阴影部分的面积等于两个扇形的面积和减去长方形的面积;据此解答即可。
【详解】3.14×62÷4+3.14×42÷4-6×4
=28.26+12.56-24
=16.82(平方厘米)
17.12.56立方厘米
【分析】通过观察图形可知,旋转后形成圆锥的底面半径是2厘米,高是3厘米,根据圆锥的体积公式:V=r2h,把数据代入公式解答。
【详解】×3.14×22×3
=×3.14×4×3
=12.56(立方厘米)
所以,形成图形的体积是12.56立方厘米。
18.62.8平方厘米
【分析】将一个直角梯形绕着线段AB所在的轴旋转一周,求旋转一周后形成的图形是外面是一个圆柱,里面有个倒放的圆锥,如图:,根据圆柱的体积公式:V=πr2h,圆锥的体积公式:V=πr2h,分别求出圆柱和圆锥的体积,然后相减即可。
【详解】3.14××6
=3.14×4×6
=12.56×6
=75.36(平方厘米)
×3.14××(6-3)
=×3.14×4×3
=×37.68
=12.56(平方厘米)
75.36-12.56=62.8(平方厘米)
19.392.5cm3
【分析】观察可知,已知圆锥的底面直径是10cm,高是15cm,根据半径=直径÷2,圆锥的体积公式,代入数据计算即可。
【详解】
(cm3)
20.125.6cm3;125.6cm3
【分析】左图:用圆柱的体积加上圆锥的体积,求出组合体的体积;
右图:将大圆柱的体积减去小圆柱的体积,求出这个几何体的体积。
【详解】3.14×22×8+×3.14×22×6
=100.48+25.12
=125.6(cm3)
3.14×(6÷2)2×8-3.14×(4÷2)2×8
=3.14×72-3.14×32
=3.14×(72-32)
=3.14×40
=125.6(cm3)
所以,这两个几何体的体积都是125.6cm3。
21.3925立方厘米
【分析】图中的零件可看作一个圆柱被斜着切成两段,两段的体积相等,所以这个圆柱的底面直径为10厘米,高为(54+46)厘米,利用圆柱的体积公式:V=,代入求出圆柱的体积,再除以2,即可求出这个零件的体积。
【详解】3.14×(10÷2)2×(54+46)÷2
=3.14×52×100÷2
=3.14×25×100÷2
=78.5×100÷2
=3925(立方厘米)
22.11140立方分米
【分析】根据图示,可以先求出下面正方体的体积,然后加上上面个圆柱的体积解答。上面圆柱的直径是20分米,高是20分米,根据圆柱的体积公式求出圆柱的体积后,再除以2,求出个圆柱的体积,再加上正方体的体积解答即可。
【详解】20×20×20+3.14×(20÷2)2×20÷2
=8000+3.14×100×20÷2
=8000+3140
=11140(立方分米)
23.25.12平方厘米
【分析】根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高,根据圆柱的表面积公式:S表=S侧+S底×2,把数据代入公式解答。
【详解】6.28×3+3.14×(6.28÷3.14÷2)2×2
=18.84+3.14×1×2
=18.84+6.28
=25.12(平方厘米)
所以,这个圆柱的表面积是25.12平方厘米。
24.1978.2立方厘米
【分析】由图意知:立体图形的体积是直径为10的圆柱体积减直径为4的同心圆柱的体积,据此解答。
【详解】3.14×(10÷2)2×30-3.14×(4÷2)2×30
=3.14×25×30-3.14×4×30
=2355-376.8
=1978.2(立方厘米)
【点睛】掌握圆柱体的体积计算公式是解答本题的关键。
25.295.36dm2
【分析】通过观察图形可知,由于上面的圆柱与下面的长方体粘合在一起,所以上面的圆柱只求它的侧面积,下面的长方体求它的表面积,然后合并起来。根据圆柱的侧面积公式:S=πdh,长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【详解】3.14×4×6+(10×4+10×5+4×5)×2
=12.56×6+(40+50+20)×2
=75.36+110×2
=75.36+220
=295.36(dm2)
答案第1页,共2页
21世纪教育网(www.21cnjy.com)
答案第1页,共2页
小升初数学备考真题分类汇编(山西地区专版)
一、平面图形
(一)组合图形周长及面积计算
(2023·山西长治·小升初真题)
1.求下面梯形和半圆的面积(单位:厘米)。
(2024·山西长治·小升初真题)
2.计算下面图形的面积。(单位:cm)
(2024·山西太原·小升初真题)
3.求出下面两图形的周长。(单位:厘米)
(2024·山西大同·小升初真题)
4.求图的周长。
(2023·山西吕梁·小升初真题)
5.看图列式计算,求如图椭圆形操场的周长和面积。
(2023·山西晋中·小升初真题)
6.如图,计算它的周长和面积。(单位:厘米)
(二)组合图形阴影部分面积计算
(2022·山西太原·小升初真题)
7.计算下面阴影部分的面积。(单位:厘米)
(2021·山西太原·小升初真题)
8.求涂色部分的面积。
(2024·山西阳泉·小升初真题)
9.计算下面图形中阴影部分的面积。
(2024·山西运城·小升初真题)
10.如图,两个相同的直角梯形重叠在一起,已知CM=5cm,GM=8cm,GH=20cm,求阴影部分的面积。
(2024·山西朔州·小升初真题)
11.求阴影部分的面积(单位:cm)。
(2022·山西运城·小升初真题)
12.求如图阴影部分的面积。(单位:厘米)
(2023·山西朔州·小升初真题)
13.求图形中阴影部分的面积(单位:厘米)
2厘米
(2024·山西晋城·小升初真题)
14.看图列式计算,求涂色部分的面积.(单位:厘米)
(2023·山西晋城·小升初真题)
15.求阴影部分的面积(单位:米)。
(2022·山西晋城·小升初真题)
16.如图(单位:厘米),四边形ABCD是长方形,其中弧AE以点B为圆心,AB的长为半径,弧AF的点D为圆心,AD的长为半径。计算阴影部分的面积。
二、立体图形
(2023·山西长治·小升初真题)
17.求出如图中三角形绕直角边旋转一周后形成图形的体积。
(2022·山西长治·小升初真题)
18.如图,将一个直角梯形绕着线段AB所在的轴旋转一周,求旋转一周后形成的图形的体积。
(2024·山西吕梁·小升初真题)
19.计算如图的体积。
(2024·山西大同·小升初真题)
20.求下列图形的体积。
(2023·山西大同·小升初真题)
21.一个零件的形状如下图所示,求这个零件的体积。
(2024·山西·小升初真题)
22.求下面立体图形的体积(单位:分米)
(2023·山西临汾·小升初真题)
23.如图是圆柱体的表面展开图,请计算出这个圆柱的表面积。
(2024·山西忻州·小升初真题)
24.计算下图的体积。(单位:cm)
(2023·山西忻州·小升初真题)
25.计算下面图形的表面积。
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
试卷第1页,共3页
《2024-2025学年山西省人教版六年级下册小升初备考真题分类汇编专题05 图形计算数学试卷》参考答案:
1.7平方厘米;25.12平方厘米
【详解】梯形的面积:
×2×(2+5)
=×2×7
=7(平方厘米)
圆的面积:
×3.14×()2
=×3.14×16
=25.12(平方厘米)
2.15.6
【详解】3.2×3.5÷2
=11.2÷2
=5.6()
(3.2+4.8)×2.5÷2
=8×2.5÷2
=10()
5.6+10=15.6()
3.37.68厘米;35.7厘米
【分析】根据圆的周长=πd,代入数据即可解答;
图形的周长=πr+4r,代入数据即可解答。
【详解】3.14×12=37.68(厘米)
3.14×5+5×4
=15.7+20
=35.7(厘米)
4.228.5厘米
【分析】观察图形可知,这个图形的周长等于3条50厘米的线段之和,再加上直径50厘米的圆的周长的一半,据此利用圆的周长公式计算即可解答。
【详解】50×3+3.14×50÷2
=150+78.5
=228.5(厘米)
图的周长是228.5厘米。
5.周长是400.96m,面积是9615.36m2
【分析】(1)椭圆形操场的周长等于两个圆弧的长加上长方形的两条长,即半径是32米的圆的周长加上长方形的两条长。
(2)椭圆形操场的面积等于长方形的面积加上两个半圆,即长方形的面积加上半径是32米的圆的面积。
【详解】(1)椭圆形操场的周长为:
2×3.14×32+100×2
=200.96+200
=400.96(m)
(2)椭圆形操场的面积为:
3.14×322+100×(32×2)
=3.14×1024+100×64
=3215.36+6400
=9615.36(m2)
椭圆形操场的周长是400.96m,面积是9615.36m2。
【点睛】此题主要考查了组合图形的周长和面积的求法,解答此题的关键是熟练掌握长方形、圆的周长和面积公式。
6.图形的周长是10.28厘米,面积是6.28平方厘米
【分析】图形的周长等于圆的周长的一半再加上一条直径的长度,直径的长度已知,从而问题得解。半圆的面积等于圆的面积的一半,利用圆的面积公式即可得解。
【详解】周长:3.14×4÷2+4
=12.56÷2+4
=6.28+4
=10.28(厘米)
面积:3.14×(4÷2)2÷2
=3.14×4÷2
=12.56÷2
=6.28(平方厘米)
图形的周长是10.28厘米,面积是6.28平方厘米。
【点睛】此题主要考查圆的周长和面积的计算方法,关键是计算周长时别忘了加直径。
7.50
【详解】8×8÷2+6×6÷2
=32+18
=50()
答:阴影部分的面积是50。
8.60.75cm2
【分析】涂色部分的面积=梯形面积-半圆的面积,根据梯形面积=(上底+下底)×高÷2,圆的面积公式:S=πr2,代入数据求解即可。
【详解】(6+14)×10÷2-3.14×(10÷2)2÷2
=100-39.25
=60.75(cm2)
9.13.5平方厘米
【分析】如下图,把右边的阴影部分移补到如箭头所示的左边空白部分,这样阴影部分合并成一个梯形,梯形的上底是(6-3)厘米,下底是6厘米,高是3厘米,根据梯形的面积=(上底+下底)×高÷2,代入数据计算求出阴影部分的面积。
【详解】(6-3+6)×3÷2
=9×3÷2
=13.5(平方厘米)
阴影部分的面积是13.5平方厘米。
10.140平方厘米
【分析】通过观察图形可知,阴影部分的面积=S梯形ABCD-S梯形EFMD,S梯形DMGH=S梯形EFGH-S梯形EFMD,S梯形ABCD和S梯形EFGH是两个相同的直角梯形,故阴影部分的面积和梯形DMGH的面积相等,阴影部分转化为梯形DMGH的面积,根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式解答。
【详解】根据分析可得:
S阴影部分的面积=S梯形DMGH
(平方厘米)
因此,阴影部分的面积是140平方厘米。
11.2cm2
【分析】观察图形可知,阴影部分是一个底为2cm、高为2cm的三角形,根据三角形的面积=底×高÷2,代入数据计算求出阴影部分的面积。
【详解】2×2÷2=2(cm2)
阴影部分的面积是2cm2。
12.26.52平方厘米
【分析】由图可知:阴影部分的面积=半圆的面积-三角形的面积,代入数据计算即可。
【详解】
=3.14×36÷2
=113.04÷2
=56.52(平方厘米)
=60÷2
=30(平方厘米)
56.52-30=26.52(平方厘米)
13.2.28平方厘米
【分析】通过切拼(如下图),即可得阴影部分的面积=半圆的面积-三角形的面积,已知半圆的半径是2厘米,三角形的底是2+2=4(厘米),高是2厘米,根据半圆的面积:S=π22÷2,三角形的面积=底×高÷2,分别代入数据计算,再相减即可。
【详解】
2厘米
22×3.14÷2-4×2÷2
=4×3.14÷2-4×2÷2
=12.56÷2-4×2÷2
=6.28-4×2÷2
=6.28-8÷2
=6.28-4
=2.28(平方厘米)
阴影部分的面积是2.28平方厘米。
14.(1)22平方厘米.
(2)13.74平方厘米
【分析】(1)阴影部分是梯形,根据空白部分的面积和底,可求出空白部分的高,也就是梯形的高,代入梯形的面积公式即可求出阴影部分的面积.(2)梯形的面积减去四分之一圆的面积就是阴影部分的面积,梯形的上底和高等于四分之一圆的半径,下底是8厘米,代入公式计算即可.
【详解】(1)10×2÷5=4(厘米)
(3+3+5)×4÷2
=11×4÷2
=22(平方厘米)
答:涂色部分的面积是22平方厘米.
(2)(6+8)×6÷2﹣3.14×62÷4
=14×6÷2﹣28.26
=42﹣28.26
=13.74(平方厘米)
答:涂色部分的面积是13.74平方厘米
15.6平方米
【分析】根据等腰三角形的特征,等腰三角形的两条腰的长度相等,再根据三角形的面积公式:S=ah÷2,阴影部分的面积等于大三角形的面积与小三角形的面积差,把数据代入公式解答。
【详解】4×4÷2﹣2×2÷2
=8﹣2
=6(平方米)
答:阴影部分的面积是6平方米。
16.16.82平方厘米
【分析】阴影部分的面积等于两个扇形的面积和减去长方形的面积;据此解答即可。
【详解】3.14×62÷4+3.14×42÷4-6×4
=28.26+12.56-24
=16.82(平方厘米)
17.12.56立方厘米
【分析】通过观察图形可知,旋转后形成圆锥的底面半径是2厘米,高是3厘米,根据圆锥的体积公式:V=r2h,把数据代入公式解答。
【详解】×3.14×22×3
=×3.14×4×3
=12.56(立方厘米)
所以,形成图形的体积是12.56立方厘米。
18.62.8平方厘米
【分析】将一个直角梯形绕着线段AB所在的轴旋转一周,求旋转一周后形成的图形是外面是一个圆柱,里面有个倒放的圆锥,如图:,根据圆柱的体积公式:V=πr2h,圆锥的体积公式:V=πr2h,分别求出圆柱和圆锥的体积,然后相减即可。
【详解】3.14××6
=3.14×4×6
=12.56×6
=75.36(平方厘米)
×3.14××(6-3)
=×3.14×4×3
=×37.68
=12.56(平方厘米)
75.36-12.56=62.8(平方厘米)
19.392.5cm3
【分析】观察可知,已知圆锥的底面直径是10cm,高是15cm,根据半径=直径÷2,圆锥的体积公式,代入数据计算即可。
【详解】
(cm3)
20.125.6cm3;125.6cm3
【分析】左图:用圆柱的体积加上圆锥的体积,求出组合体的体积;
右图:将大圆柱的体积减去小圆柱的体积,求出这个几何体的体积。
【详解】3.14×22×8+×3.14×22×6
=100.48+25.12
=125.6(cm3)
3.14×(6÷2)2×8-3.14×(4÷2)2×8
=3.14×72-3.14×32
=3.14×(72-32)
=3.14×40
=125.6(cm3)
所以,这两个几何体的体积都是125.6cm3。
21.3925立方厘米
【分析】图中的零件可看作一个圆柱被斜着切成两段,两段的体积相等,所以这个圆柱的底面直径为10厘米,高为(54+46)厘米,利用圆柱的体积公式:V=,代入求出圆柱的体积,再除以2,即可求出这个零件的体积。
【详解】3.14×(10÷2)2×(54+46)÷2
=3.14×52×100÷2
=3.14×25×100÷2
=78.5×100÷2
=3925(立方厘米)
22.11140立方分米
【分析】根据图示,可以先求出下面正方体的体积,然后加上上面个圆柱的体积解答。上面圆柱的直径是20分米,高是20分米,根据圆柱的体积公式求出圆柱的体积后,再除以2,求出个圆柱的体积,再加上正方体的体积解答即可。
【详解】20×20×20+3.14×(20÷2)2×20÷2
=8000+3.14×100×20÷2
=8000+3140
=11140(立方分米)
23.25.12平方厘米
【分析】根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高,根据圆柱的表面积公式:S表=S侧+S底×2,把数据代入公式解答。
【详解】6.28×3+3.14×(6.28÷3.14÷2)2×2
=18.84+3.14×1×2
=18.84+6.28
=25.12(平方厘米)
所以,这个圆柱的表面积是25.12平方厘米。
24.1978.2立方厘米
【分析】由图意知:立体图形的体积是直径为10的圆柱体积减直径为4的同心圆柱的体积,据此解答。
【详解】3.14×(10÷2)2×30-3.14×(4÷2)2×30
=3.14×25×30-3.14×4×30
=2355-376.8
=1978.2(立方厘米)
【点睛】掌握圆柱体的体积计算公式是解答本题的关键。
25.295.36dm2
【分析】通过观察图形可知,由于上面的圆柱与下面的长方体粘合在一起,所以上面的圆柱只求它的侧面积,下面的长方体求它的表面积,然后合并起来。根据圆柱的侧面积公式:S=πdh,长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【详解】3.14×4×6+(10×4+10×5+4×5)×2
=12.56×6+(40+50+20)×2
=75.36+110×2
=75.36+220
=295.36(dm2)
答案第1页,共2页
21世纪教育网(www.21cnjy.com)
答案第1页,共2页
同课章节目录
