人教版八年级数学下册 课件:16.2 二次根式的乘除(共44张PPT)
文档属性
| 名称 | 人教版八年级数学下册 课件:16.2 二次根式的乘除(共44张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 939.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-06 21:13:31 | ||
图片预览










文档简介
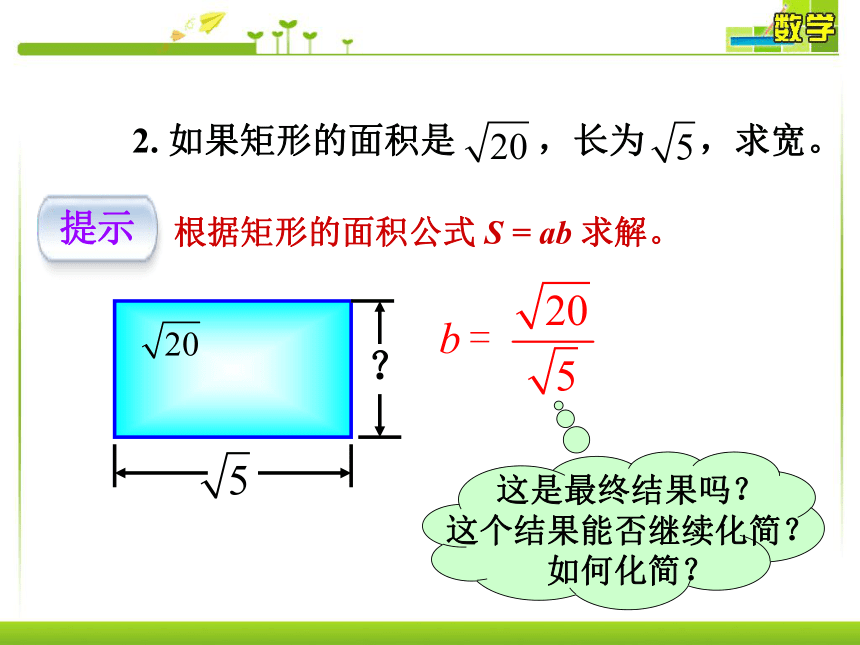
课件44张PPT。 1. 一个平行四边形的底为 ,高为 ,求这个平行四边形的面积。根据平行四边形的面积公式 S = ah 求解。提示这是最终结果吗?
这个结果能否继续化简?
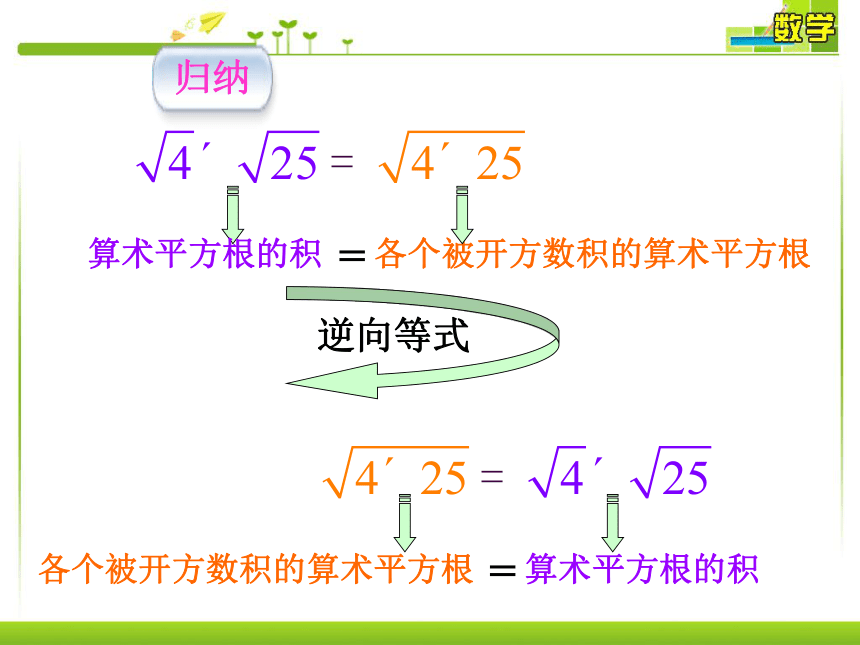
如何化简? 新课导入 2. 如果矩形的面积是 ,长为 ,求宽。根据矩形的面积公式 S = ab 求解。提示这是最终结果吗?
这个结果能否继续化简?
如何化简? 16.2二次根式的乘除 【知识与能力】
理解 (a≥0,b≥0),
( a≥0,b≥0),并利用它们进行计算和化简。
理解 (a≥0,b > 0) 和 ( a≥0,b > 0),及利用它们进行运算。
理解最简二次根式的概念,并运用它化简二次根式。 教学目标 【过程与方法】
利用具体数据探究,不完全归纳法得出二次根式的乘(除)法规律。
使用逆向思维,得出二次根式乘(除)法规律的逆向等式。
分析结果,抓住它们的共同点,给出最简二次根式的概念。 【情感态度与价值观】
利用规定准确计算和化简的严谨的科学精神。(a≥0,b≥0)(a≥0,b > 0)(a≥0,b≥0)(a≥0,b > 0)利用以上公式进行计算和化简。教学重难点1. 计算:有什么规律?有什么规律?利用计算器计算演示2. 填空:算术平方根的积各个被开方数积的算术平方根=各个被开方数积的算术平方根算术平方根的积=逆向等式归纳 下面的等式成立吗?为什么?×√×根号下不能出现负数!(a≥0,b≥0)(a≥0,b≥0)a、b必须都是非负数!二次根式的乘法规定:逆向等式:可以进行二次根式的化简。计算:(2)(1)化简:(1)(2)16 ,b2 ,c2 , 是开得尽的因数或因式。计算:(1)一题多解(2)一题多解1. 计算:有什么规律?有什么规律?利用计算器计算演示2. 填空:算术平方根的商各个被开方数商的算术平方根=各个被开方数商的算术平方根算术平方根的商=逆向等式归纳 下面的等式成立吗?为什么?×√根号下不能出现负数!×分母不能为0 !二次根式的除法规定:逆向等式:可以进行二次根式的化简。(a≥0,b > 0)(a≥0,b > 0)化简:(2)(1)计算:(1)一题多解(2)为了去掉分母中的根号最后结果的分母中不含二次根式。(3)(4)为了去掉分母中的根号最后结果的分母中不含二次根式。分母有理化 把分母中的根号化去,使分母变成有理数,这个过程叫做分母有理化。 2. 分母有理化的关键是要搞清分式的分子和分母都乘什么。注意 1. 在二次根式的运算中,一般先观察把能化简的二次根式化简,再考虑如何化去分母中的根号。最简二次根式的特点 被开方数不含分母。
被开方数中不含能开得尽方的因数或因式。以上各例题的最后结果: 分母中不含二次根式。
被开方数不能含有小数或分数。
分子分母不能约分。
最后结果中的二次根式要求化成最简二次根式。在二次根式的运算中, 最后结果的一般要求×××× 看谁算得快化简 。1.将被开方数尽可能分解成几个平方数.2.应用 3.将平方式(或平方数)应用 把这个因式(或因数)开出来,将二次根式化简。化简二次根式的步骤 在Rt△ABC中,∠C = 90°, BC = 1.5 cm ,AC = 3 cm,求斜边 AB 的长。解答:CAB3 cm?1.5 cm解:由勾股定理AB2 = AC2+BC2 ,∴ AB = CAB3 cm?1.5 cm(cm)1. 二次根式的乘法:课堂小结2. 二次根式的除法有两种常用方法:(1)利用公式: (2)把除法先写成分式的形式,再进行分母有理化运算。(1)将被开方数尽可能分解成几个平方数。(2)应用 。 (3)将平方式(或平方数)应用 把这个因式(或因数)开出来,将二次根式化简。3. 化简二次根式的步骤: 1. 判断下列算法是否正确,不正确的请予以改正。××随堂练习正确的算法如下:m > 5 2. 等式 成立的条件是____________。解:要想等式成立,必须满足:m-3 ≥0m-5 > 0m ≥3m > 5m > 5 3. 已知: =1.732,如何求出 的近似值?一题多解计算繁琐。计算简便。(4) 4.在括号内填写适当的数或式子使等式成立。 5. 化简。6. 已知实数 a、b 满足求 的值。解:要想原等式有意义,必须满足:将 a、b 代入 7. 判断下列各式是否为最简二次根式?√习题答案(1) (2) (3) (4)
(1) (2) (3) (4)
(1) (2) (3) (4)
(1) (2)
这个结果能否继续化简?
如何化简? 新课导入 2. 如果矩形的面积是 ,长为 ,求宽。根据矩形的面积公式 S = ab 求解。提示这是最终结果吗?
这个结果能否继续化简?
如何化简? 16.2二次根式的乘除 【知识与能力】
理解 (a≥0,b≥0),
( a≥0,b≥0),并利用它们进行计算和化简。
理解 (a≥0,b > 0) 和 ( a≥0,b > 0),及利用它们进行运算。
理解最简二次根式的概念,并运用它化简二次根式。 教学目标 【过程与方法】
利用具体数据探究,不完全归纳法得出二次根式的乘(除)法规律。
使用逆向思维,得出二次根式乘(除)法规律的逆向等式。
分析结果,抓住它们的共同点,给出最简二次根式的概念。 【情感态度与价值观】
利用规定准确计算和化简的严谨的科学精神。(a≥0,b≥0)(a≥0,b > 0)(a≥0,b≥0)(a≥0,b > 0)利用以上公式进行计算和化简。教学重难点1. 计算:有什么规律?有什么规律?利用计算器计算演示2. 填空:算术平方根的积各个被开方数积的算术平方根=各个被开方数积的算术平方根算术平方根的积=逆向等式归纳 下面的等式成立吗?为什么?×√×根号下不能出现负数!(a≥0,b≥0)(a≥0,b≥0)a、b必须都是非负数!二次根式的乘法规定:逆向等式:可以进行二次根式的化简。计算:(2)(1)化简:(1)(2)16 ,b2 ,c2 , 是开得尽的因数或因式。计算:(1)一题多解(2)一题多解1. 计算:有什么规律?有什么规律?利用计算器计算演示2. 填空:算术平方根的商各个被开方数商的算术平方根=各个被开方数商的算术平方根算术平方根的商=逆向等式归纳 下面的等式成立吗?为什么?×√根号下不能出现负数!×分母不能为0 !二次根式的除法规定:逆向等式:可以进行二次根式的化简。(a≥0,b > 0)(a≥0,b > 0)化简:(2)(1)计算:(1)一题多解(2)为了去掉分母中的根号最后结果的分母中不含二次根式。(3)(4)为了去掉分母中的根号最后结果的分母中不含二次根式。分母有理化 把分母中的根号化去,使分母变成有理数,这个过程叫做分母有理化。 2. 分母有理化的关键是要搞清分式的分子和分母都乘什么。注意 1. 在二次根式的运算中,一般先观察把能化简的二次根式化简,再考虑如何化去分母中的根号。最简二次根式的特点 被开方数不含分母。
被开方数中不含能开得尽方的因数或因式。以上各例题的最后结果: 分母中不含二次根式。
被开方数不能含有小数或分数。
分子分母不能约分。
最后结果中的二次根式要求化成最简二次根式。在二次根式的运算中, 最后结果的一般要求×××× 看谁算得快化简 。1.将被开方数尽可能分解成几个平方数.2.应用 3.将平方式(或平方数)应用 把这个因式(或因数)开出来,将二次根式化简。化简二次根式的步骤 在Rt△ABC中,∠C = 90°, BC = 1.5 cm ,AC = 3 cm,求斜边 AB 的长。解答:CAB3 cm?1.5 cm解:由勾股定理AB2 = AC2+BC2 ,∴ AB = CAB3 cm?1.5 cm(cm)1. 二次根式的乘法:课堂小结2. 二次根式的除法有两种常用方法:(1)利用公式: (2)把除法先写成分式的形式,再进行分母有理化运算。(1)将被开方数尽可能分解成几个平方数。(2)应用 。 (3)将平方式(或平方数)应用 把这个因式(或因数)开出来,将二次根式化简。3. 化简二次根式的步骤: 1. 判断下列算法是否正确,不正确的请予以改正。××随堂练习正确的算法如下:m > 5 2. 等式 成立的条件是____________。解:要想等式成立,必须满足:m-3 ≥0m-5 > 0m ≥3m > 5m > 5 3. 已知: =1.732,如何求出 的近似值?一题多解计算繁琐。计算简便。(4) 4.在括号内填写适当的数或式子使等式成立。 5. 化简。6. 已知实数 a、b 满足求 的值。解:要想原等式有意义,必须满足:将 a、b 代入 7. 判断下列各式是否为最简二次根式?√习题答案(1) (2) (3) (4)
(1) (2) (3) (4)
(1) (2) (3) (4)
(1) (2)
