24.4《三角形的中位线》
图片预览



文档简介
课件19张PPT。 明江中学副校长 黄灿喜 课题 §24.4三角形的中位线华师大九年级数学(上) 执教者:黄灿喜学习重点:三角形中位线定理的探究过程及应用。
学习难点:三角形中位线性质定理证明中添加补助线的思想方法。学习目标:
1.理解三角形中位线的定义,并掌握它的性质定理。
2. 初步运用三角形的中位线定理进行求解与推理。 在△ABC 中,D是BC的中点,则AD是△ABC的 ; △ABC的中线有 ,请你把它们画出来。
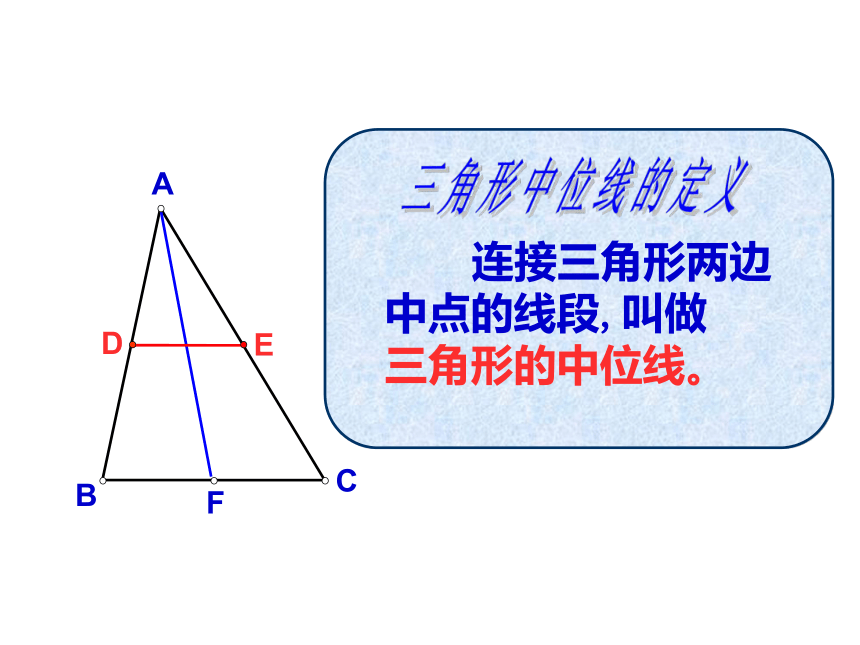
你还记得吗?DABC中线三条CBAFED 连接三角形两边中点的线段,叫做 三角形的中位线。
三角形中位线的定义
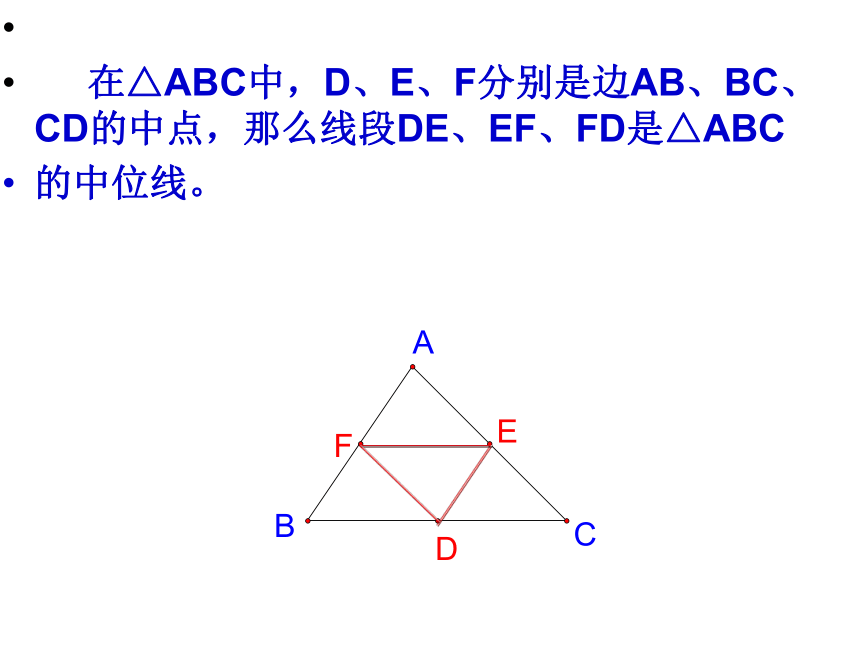
在△ABC中,D、E、F分别是边AB、BC、CD的中点,那么线段DE、EF、FD是△ABC
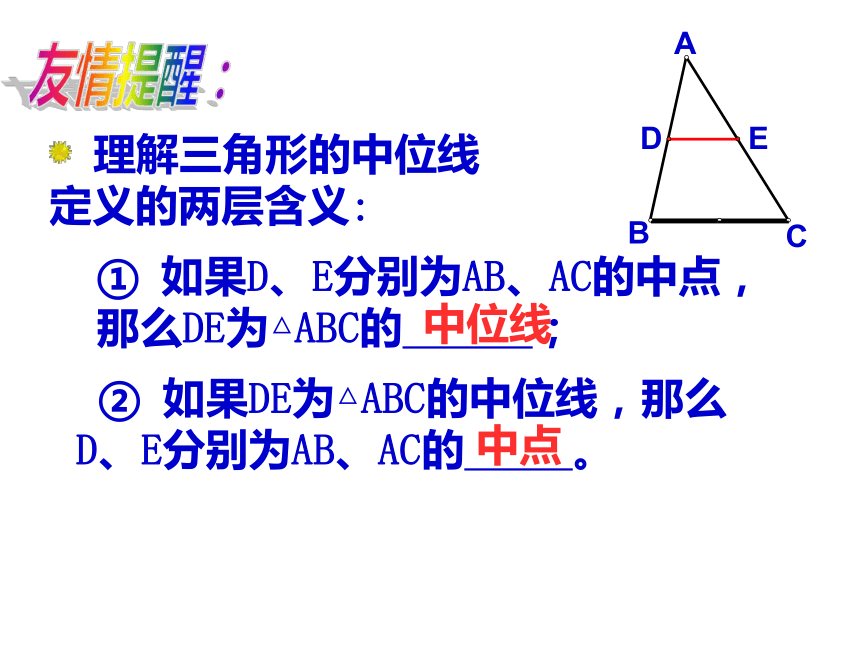
的中位线。EFDABC友情提醒: 理解三角形的中位线定义的两层含义: ② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。① 如果D、E分别为AB、AC的中点, 那么DE为△ABC的 ;CBAED中位线中点 怎样将一张三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形??ABCDEFABCDEF 四边形BCFD是平行四边形吗?为什么? 三角形的中位线平行于第三边,并且等于它的一半。 DE是△ABC的中位线,猜想DE与BC有怎样的位置关系和数量关系?为什么?ABCDEF三角形中位线定理 A、B两点被池塘隔开,如何才能知道它们之间的距离呢? 在AB外选一点C,连结AC和BC,并分别找出AC和BC的中点M、N,如果测得MN = 20m,那么A、B两点的距离是多少?为什么?说一说CBA2040如图1:在△ABC中,DE是中位线
(1)若∠ADE=56°,
则∠B= 度,为什么?
(2)若BC=10cm,
则DE= cm,为什么? 如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm图1图256512ABCD EBACD EF543例1 求证三角形的一条中位线与第三边上的中线互相平分.已知: 如图24.4.3所示,在△ABC中,AD=DB,BE=EC,AF=FC.
求证: AE、DF互相平分.证明 连结DE、EF.
∵ AD=DB,BE=EC,
∴ DE∥AC(三角形的中位线平行于第三边并且等于第三边的一半).
同理EF∥AB.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分(平行四边形的对角线互相平分). 例2 如图24.4.4,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.
求证: 证明 :连结ED, ∵ D、E分别是边BC、AB的中点,∴ DE∥AC,(三角形的中位线平行于第三边并且等于第三边的一半), ∴ △ACG∽△DEG,∴ ∴ 拓展如果在图24.4.4中,取AC的中点F,假设BF与AD交于G′,如图24.4.5,那么我们
同理有 ,所以
有 ,即两图中的点G与G′是重合的. 三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线
的长是对应中线长的
.请思考:
(1)在△ABC中,AD是BC边上的中线,G是重心。如果AG=6 ,那么线段DG的长是多少?
(2)已知 △ABC的三条中位线组成的三角形的周长为26厘米,则 △ABC的周长为 是多少? 说一说你学到了什么?布置作业1、练习 第1题
2、习题24.4 第1题 祝同学们学习愉快
学习难点:三角形中位线性质定理证明中添加补助线的思想方法。学习目标:
1.理解三角形中位线的定义,并掌握它的性质定理。
2. 初步运用三角形的中位线定理进行求解与推理。 在△ABC 中,D是BC的中点,则AD是△ABC的 ; △ABC的中线有 ,请你把它们画出来。
你还记得吗?DABC中线三条CBAFED 连接三角形两边中点的线段,叫做 三角形的中位线。
三角形中位线的定义
在△ABC中,D、E、F分别是边AB、BC、CD的中点,那么线段DE、EF、FD是△ABC
的中位线。EFDABC友情提醒: 理解三角形的中位线定义的两层含义: ② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。① 如果D、E分别为AB、AC的中点, 那么DE为△ABC的 ;CBAED中位线中点 怎样将一张三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形??ABCDEFABCDEF 四边形BCFD是平行四边形吗?为什么? 三角形的中位线平行于第三边,并且等于它的一半。 DE是△ABC的中位线,猜想DE与BC有怎样的位置关系和数量关系?为什么?ABCDEF三角形中位线定理 A、B两点被池塘隔开,如何才能知道它们之间的距离呢? 在AB外选一点C,连结AC和BC,并分别找出AC和BC的中点M、N,如果测得MN = 20m,那么A、B两点的距离是多少?为什么?说一说CBA2040如图1:在△ABC中,DE是中位线
(1)若∠ADE=56°,
则∠B= 度,为什么?
(2)若BC=10cm,
则DE= cm,为什么? 如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm图1图256512ABCD EBACD EF543例1 求证三角形的一条中位线与第三边上的中线互相平分.已知: 如图24.4.3所示,在△ABC中,AD=DB,BE=EC,AF=FC.
求证: AE、DF互相平分.证明 连结DE、EF.
∵ AD=DB,BE=EC,
∴ DE∥AC(三角形的中位线平行于第三边并且等于第三边的一半).
同理EF∥AB.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分(平行四边形的对角线互相平分). 例2 如图24.4.4,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.
求证: 证明 :连结ED, ∵ D、E分别是边BC、AB的中点,∴ DE∥AC,(三角形的中位线平行于第三边并且等于第三边的一半), ∴ △ACG∽△DEG,∴ ∴ 拓展如果在图24.4.4中,取AC的中点F,假设BF与AD交于G′,如图24.4.5,那么我们
同理有 ,所以
有 ,即两图中的点G与G′是重合的. 三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线
的长是对应中线长的
.请思考:
(1)在△ABC中,AD是BC边上的中线,G是重心。如果AG=6 ,那么线段DG的长是多少?
(2)已知 △ABC的三条中位线组成的三角形的周长为26厘米,则 △ABC的周长为 是多少? 说一说你学到了什么?布置作业1、练习 第1题
2、习题24.4 第1题 祝同学们学习愉快
