24.1.2 垂直于弦的直径 同步练习(含答案)
文档属性
| 名称 | 24.1.2 垂直于弦的直径 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-09 10:47:19 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
24.1.2 垂直于弦的直径
一、单选题
1.(2022九上·婺城月考)如图,为的直径.弦于点E,,,则的值为( )
A. B. C. D.
2.(2024九上·湖北月考)如图,的直径,弦于点,若,则的长为( )
A.4 B.3 C.2 D.1
3.(2023九上·大石桥期中)已知:如图,是的直径,弦交于E点,,则的长为( )
A. B. C. D.4
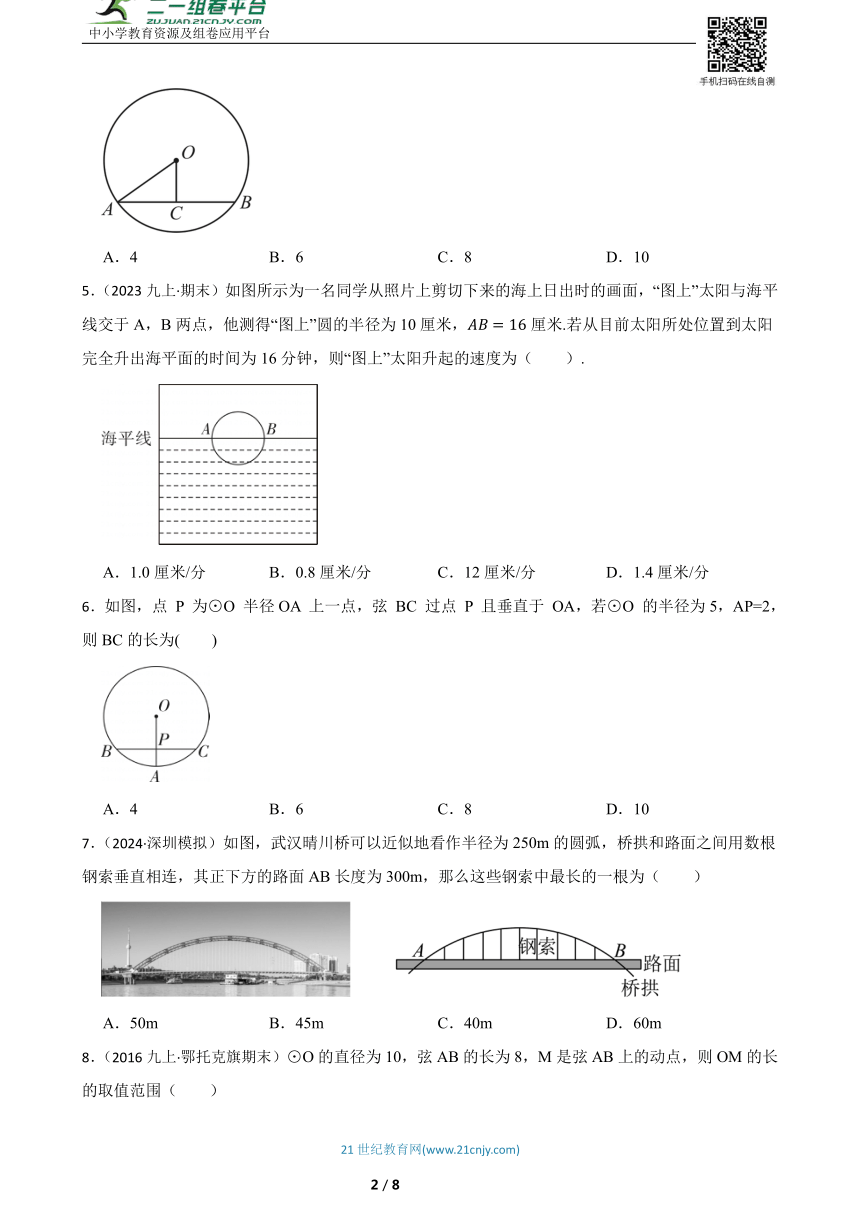
4.(2024九下·北京市开学考)如图,是的弦,若的半径,圆心到弦的距离,则弦的长为( )
A.4 B.6 C.8 D.10
5.(2023九上·期末)如图所示为一名同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A,B两点,他测得“图上”圆的半径为10厘米,厘米.若从目前太阳所处位置到太阳完全升出海平面的时间为16分钟,则“图上”太阳升起的速度为( ).
A.1.0厘米/分 B.0.8厘米/分 C.12厘米/分 D.1.4厘米/分
6.如图,点 P 为⊙O 半径OA 上一点,弦 BC 过点 P 且垂直于 OA,若⊙O 的半径为5,AP=2,则BC的长为( )
A.4 B.6 C.8 D.10
7.(2024·深圳模拟)如图,武汉晴川桥可以近似地看作半径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB长度为300m,那么这些钢索中最长的一根为( )
A.50m B.45m C.40m D.60m
8.(2016九上·鄂托克旗期末)⊙O的直径为10,弦AB的长为8,M是弦AB上的动点,则OM的长的取值范围( )
A.3≤OM≤5 B.4≤OM≤5 C.3<OM<5 D.4<OM<5
9.(2024九上·南京月考)如图,在平面直角坐标系中,的圆心坐标是,半径为3,函数的图像被截得的弦的长为,则a的值是( )
A.4 B. C. D.
10.⊙o的半径是13,弦AB∥CD,AB=24,CD=10,则AB与CD的距离是( )
A.7 B.17 C.7或17 D.4
二、填空题
11.(2024·成都模拟)已知的半径为13,弦,则上到弦所在直线的距离为1的点有 个.
12.(2024九上·东城期中)如图1所示,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图2是一款拱门的示意图,其中拱门最下端分米,为中点,为拱门最高点,圆心在线段上,分米,则拱门所在圆半径的长为 分米.
13.(2024九下·邵东模拟)如图,在半径为的中,是的弦,是的中点,交于点.若,则 .
14.(2021九上·高港月考)如图, 的直径为 ,弦 长为 ,点P在 上运动,则 的最小值是 .
15.(2017·大冶模拟)如图,⊙O的直径AB垂直于弦CD,若∠B=30°,BC=7,则CD的长为 .
16.(2017九上·东丽期末)如图, 是半径为 的⊙ 的直径, 是圆上异于 , 的任意一点, 的平分线交⊙ 于点 ,连接 和 ,△ 的中位线所在的直线与⊙ 相交于点 、 ,则 的长是
三、计算题
17.(2024九上·昆明期末)建水紫陶,别名滇南琼玉,为中国四大名陶之一.2008年建水紫陶烧制技艺被列入第二批国家级非物质文化遗产名录.其制作过程需要几十种不同的工具,其中在一种工具名为“带刻度嘴巴架”,其形状及使用方法如图1,当制作艺人把“带刻度嘴巴架”上圆弧部分恰好贴在壶口边界时,就可以保证需要粘贴的壶嘴、壶把、壶口中心在一条直线上,图2是符合题意使用该工具时的示意图,如图3,为某紫陶壶的壶口,已知A,B两点在上,直线l过圆心O,且于点D,交于点C.若,,求这个紫砂壶的壶口半径r的长.
18.(2025九上·安定期末)如图,是的直径,弦于点E,,.求的半径.
四、解答题
19.(2023九上·天桥期中)如图,在中,直径,弦,弦,垂足分别为.
(1)求弦的长;
(2)如果,求的度数.
20.(2024九上·江源期末)点A,B,C都在上,且,若,的半径为5,连接,求的长.
21.(2020九上·赣榆期中)如图1是某奢侈品牌的香水瓶,从正面看上去(如图2),它可以近似看作⊙O割去两个弓形(由弦及其所对的弧组成的图形叫做弓形)后余下的部分与矩形ABCD组合而成的图形(点B、C在⊙O上),其中BC∥EF;从侧面看,它是扁平的,厚度为1.3cm.已知⊙O的半径为2.5cm,BC=1.4cm,AB=3.1cm,EF=3cm,求香水瓶的高度h.
22.(2023九下·三水月考)二次函数.
(1)当时,函数图象与轴交于点、,与轴交于点.
①写出函数的一个性质;
②如图1,点是第四象限内函数图象上一动点,求出点坐标,使得的面积最大;
③如图2,点为第一象限内函数图象上一动点,过点作.轴,垂足为,的外接圆与交于点,求的长度;
(2)点、为函数图象上任意两点,且.若对于时,都有,求的取值范围.
答案解析部分
1.【答案】D
【知识点】勾股定理;垂径定理
2.【答案】C
【知识点】勾股定理;垂径定理
3.【答案】A
【知识点】含30°角的直角三角形;勾股定理;垂径定理
4.【答案】C
【知识点】勾股定理;垂径定理
5.【答案】A
【知识点】垂径定理的实际应用
6.【答案】C
【知识点】勾股定理;垂径定理
7.【答案】A
【知识点】勾股定理;垂径定理的实际应用
8.【答案】A
【知识点】垂径定理的实际应用
9.【答案】B
【知识点】一次函数的概念;等腰三角形的判定与性质;勾股定理;垂径定理
10.【答案】C
【知识点】勾股定理;垂径定理
11.【答案】3
【知识点】垂径定理
12.【答案】15
【知识点】勾股定理;垂径定理的实际应用
13.【答案】
【知识点】勾股定理;垂径定理
14.【答案】3
【知识点】垂线段最短及其应用;垂径定理
15.【答案】7
【知识点】勾股定理;垂径定理
16.【答案】4
【知识点】垂径定理的实际应用
17.【答案】
【知识点】勾股定理;垂径定理
18.【答案】的半径是5.
【知识点】勾股定理;垂径定理
19.【答案】(1)8
(2)
【知识点】直角三角形全等的判定-HL;勾股定理;垂径定理
20.【答案】
【知识点】勾股定理;垂径定理
21.【答案】解:如图,过点O作 于点G,延长GO交EF于点H,连接BO、EO,
∵ ,
∴ ,
∴ , ,
根据勾股定理, , ,
∴ .
【知识点】勾股定理;垂径定理的实际应用
22.【答案】(1)①函数图象的顶点坐标为;②;③
(2)
【知识点】待定系数法求一次函数解析式;垂径定理
21世纪教育网(www.21cnjy.com)
2 / 8
24.1.2 垂直于弦的直径
一、单选题
1.(2022九上·婺城月考)如图,为的直径.弦于点E,,,则的值为( )
A. B. C. D.
2.(2024九上·湖北月考)如图,的直径,弦于点,若,则的长为( )
A.4 B.3 C.2 D.1
3.(2023九上·大石桥期中)已知:如图,是的直径,弦交于E点,,则的长为( )
A. B. C. D.4
4.(2024九下·北京市开学考)如图,是的弦,若的半径,圆心到弦的距离,则弦的长为( )
A.4 B.6 C.8 D.10
5.(2023九上·期末)如图所示为一名同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A,B两点,他测得“图上”圆的半径为10厘米,厘米.若从目前太阳所处位置到太阳完全升出海平面的时间为16分钟,则“图上”太阳升起的速度为( ).
A.1.0厘米/分 B.0.8厘米/分 C.12厘米/分 D.1.4厘米/分
6.如图,点 P 为⊙O 半径OA 上一点,弦 BC 过点 P 且垂直于 OA,若⊙O 的半径为5,AP=2,则BC的长为( )
A.4 B.6 C.8 D.10
7.(2024·深圳模拟)如图,武汉晴川桥可以近似地看作半径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB长度为300m,那么这些钢索中最长的一根为( )
A.50m B.45m C.40m D.60m
8.(2016九上·鄂托克旗期末)⊙O的直径为10,弦AB的长为8,M是弦AB上的动点,则OM的长的取值范围( )
A.3≤OM≤5 B.4≤OM≤5 C.3<OM<5 D.4<OM<5
9.(2024九上·南京月考)如图,在平面直角坐标系中,的圆心坐标是,半径为3,函数的图像被截得的弦的长为,则a的值是( )
A.4 B. C. D.
10.⊙o的半径是13,弦AB∥CD,AB=24,CD=10,则AB与CD的距离是( )
A.7 B.17 C.7或17 D.4
二、填空题
11.(2024·成都模拟)已知的半径为13,弦,则上到弦所在直线的距离为1的点有 个.
12.(2024九上·东城期中)如图1所示,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图2是一款拱门的示意图,其中拱门最下端分米,为中点,为拱门最高点,圆心在线段上,分米,则拱门所在圆半径的长为 分米.
13.(2024九下·邵东模拟)如图,在半径为的中,是的弦,是的中点,交于点.若,则 .
14.(2021九上·高港月考)如图, 的直径为 ,弦 长为 ,点P在 上运动,则 的最小值是 .
15.(2017·大冶模拟)如图,⊙O的直径AB垂直于弦CD,若∠B=30°,BC=7,则CD的长为 .
16.(2017九上·东丽期末)如图, 是半径为 的⊙ 的直径, 是圆上异于 , 的任意一点, 的平分线交⊙ 于点 ,连接 和 ,△ 的中位线所在的直线与⊙ 相交于点 、 ,则 的长是
三、计算题
17.(2024九上·昆明期末)建水紫陶,别名滇南琼玉,为中国四大名陶之一.2008年建水紫陶烧制技艺被列入第二批国家级非物质文化遗产名录.其制作过程需要几十种不同的工具,其中在一种工具名为“带刻度嘴巴架”,其形状及使用方法如图1,当制作艺人把“带刻度嘴巴架”上圆弧部分恰好贴在壶口边界时,就可以保证需要粘贴的壶嘴、壶把、壶口中心在一条直线上,图2是符合题意使用该工具时的示意图,如图3,为某紫陶壶的壶口,已知A,B两点在上,直线l过圆心O,且于点D,交于点C.若,,求这个紫砂壶的壶口半径r的长.
18.(2025九上·安定期末)如图,是的直径,弦于点E,,.求的半径.
四、解答题
19.(2023九上·天桥期中)如图,在中,直径,弦,弦,垂足分别为.
(1)求弦的长;
(2)如果,求的度数.
20.(2024九上·江源期末)点A,B,C都在上,且,若,的半径为5,连接,求的长.
21.(2020九上·赣榆期中)如图1是某奢侈品牌的香水瓶,从正面看上去(如图2),它可以近似看作⊙O割去两个弓形(由弦及其所对的弧组成的图形叫做弓形)后余下的部分与矩形ABCD组合而成的图形(点B、C在⊙O上),其中BC∥EF;从侧面看,它是扁平的,厚度为1.3cm.已知⊙O的半径为2.5cm,BC=1.4cm,AB=3.1cm,EF=3cm,求香水瓶的高度h.
22.(2023九下·三水月考)二次函数.
(1)当时,函数图象与轴交于点、,与轴交于点.
①写出函数的一个性质;
②如图1,点是第四象限内函数图象上一动点,求出点坐标,使得的面积最大;
③如图2,点为第一象限内函数图象上一动点,过点作.轴,垂足为,的外接圆与交于点,求的长度;
(2)点、为函数图象上任意两点,且.若对于时,都有,求的取值范围.
答案解析部分
1.【答案】D
【知识点】勾股定理;垂径定理
2.【答案】C
【知识点】勾股定理;垂径定理
3.【答案】A
【知识点】含30°角的直角三角形;勾股定理;垂径定理
4.【答案】C
【知识点】勾股定理;垂径定理
5.【答案】A
【知识点】垂径定理的实际应用
6.【答案】C
【知识点】勾股定理;垂径定理
7.【答案】A
【知识点】勾股定理;垂径定理的实际应用
8.【答案】A
【知识点】垂径定理的实际应用
9.【答案】B
【知识点】一次函数的概念;等腰三角形的判定与性质;勾股定理;垂径定理
10.【答案】C
【知识点】勾股定理;垂径定理
11.【答案】3
【知识点】垂径定理
12.【答案】15
【知识点】勾股定理;垂径定理的实际应用
13.【答案】
【知识点】勾股定理;垂径定理
14.【答案】3
【知识点】垂线段最短及其应用;垂径定理
15.【答案】7
【知识点】勾股定理;垂径定理
16.【答案】4
【知识点】垂径定理的实际应用
17.【答案】
【知识点】勾股定理;垂径定理
18.【答案】的半径是5.
【知识点】勾股定理;垂径定理
19.【答案】(1)8
(2)
【知识点】直角三角形全等的判定-HL;勾股定理;垂径定理
20.【答案】
【知识点】勾股定理;垂径定理
21.【答案】解:如图,过点O作 于点G,延长GO交EF于点H,连接BO、EO,
∵ ,
∴ ,
∴ , ,
根据勾股定理, , ,
∴ .
【知识点】勾股定理;垂径定理的实际应用
22.【答案】(1)①函数图象的顶点坐标为;②;③
(2)
【知识点】待定系数法求一次函数解析式;垂径定理
21世纪教育网(www.21cnjy.com)
2 / 8
同课章节目录
