24.2 点和圆、直线和圆的位置关系本节综合题(含答案)
文档属性
| 名称 | 24.2 点和圆、直线和圆的位置关系本节综合题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 511.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-09 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
24.2 点和圆、直线和圆的位置关系本节综合题
一、单选题
1.(2023九上·海宁月考)如图,在的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
A.点P B.点Q C.点R D.点M
2.应用反证法推出矛盾的推导过程中要把下列哪些作为条件使用( )
①结论的否定;②已知条件;③公理、定理、定义等;④原结论.
A.①② B.②③ C.①②③ D.①②④
3.(2023·龙港模拟)如图,与相切于点,若的半径为,,则的长为( )
A. B. C. D.4
4.若⊙O的直径为20cm,点O到直线l的距离为10cm,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法确定
5.(2024九上·遵化期末)已知⊙O的半径为4cm,A为线段OP的中点,当OP=6cm时,点A与⊙O的位置关系是( )
A.A在⊙O内 B.A在⊙O上 C.A在⊙O外 D.不能确定
6.(2023八下·高碑店期中)用反证法证明命题“在中,若,则”,首先应假设( )
A. B. C. D.
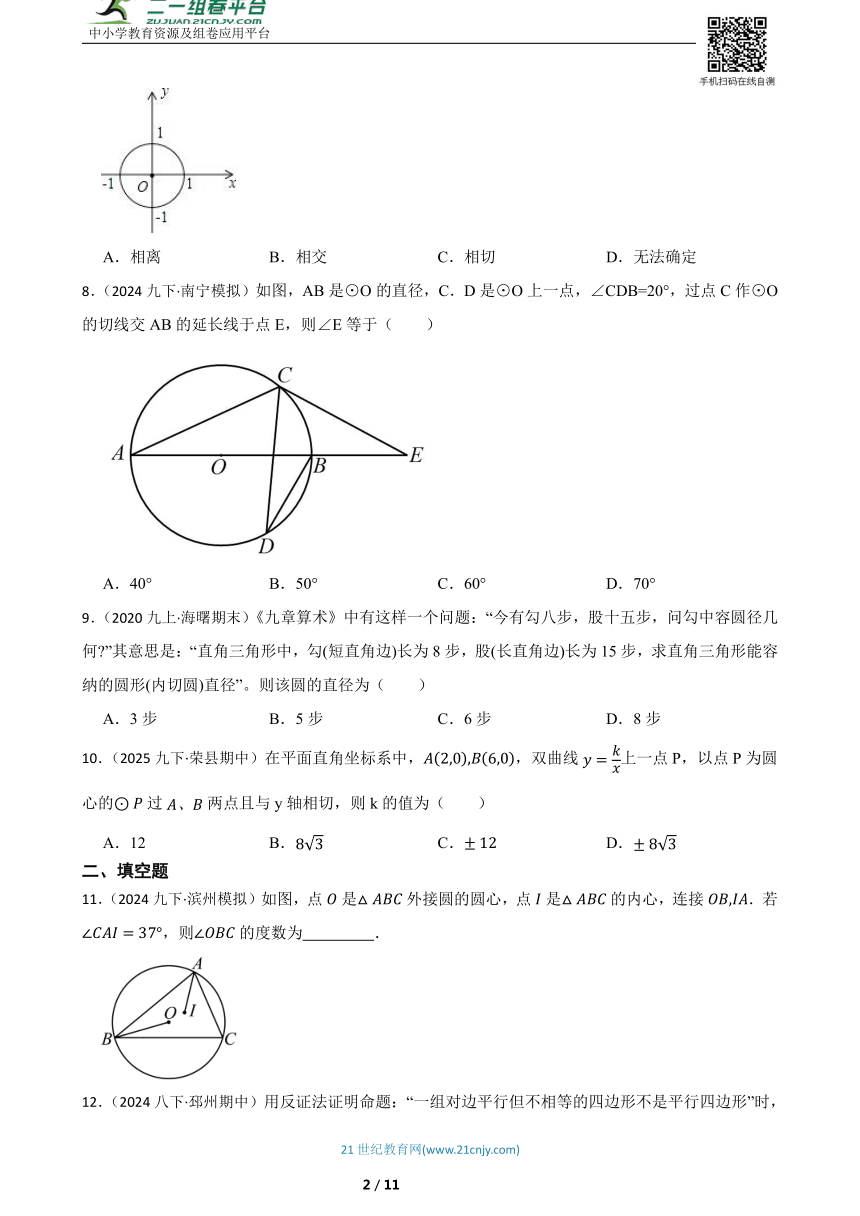
7.如图,在直角坐标系中,⊙O的半径为1,则直线y=﹣2x+ 与⊙O的位置关系是( )
A.相离 B.相交 C.相切 D.无法确定
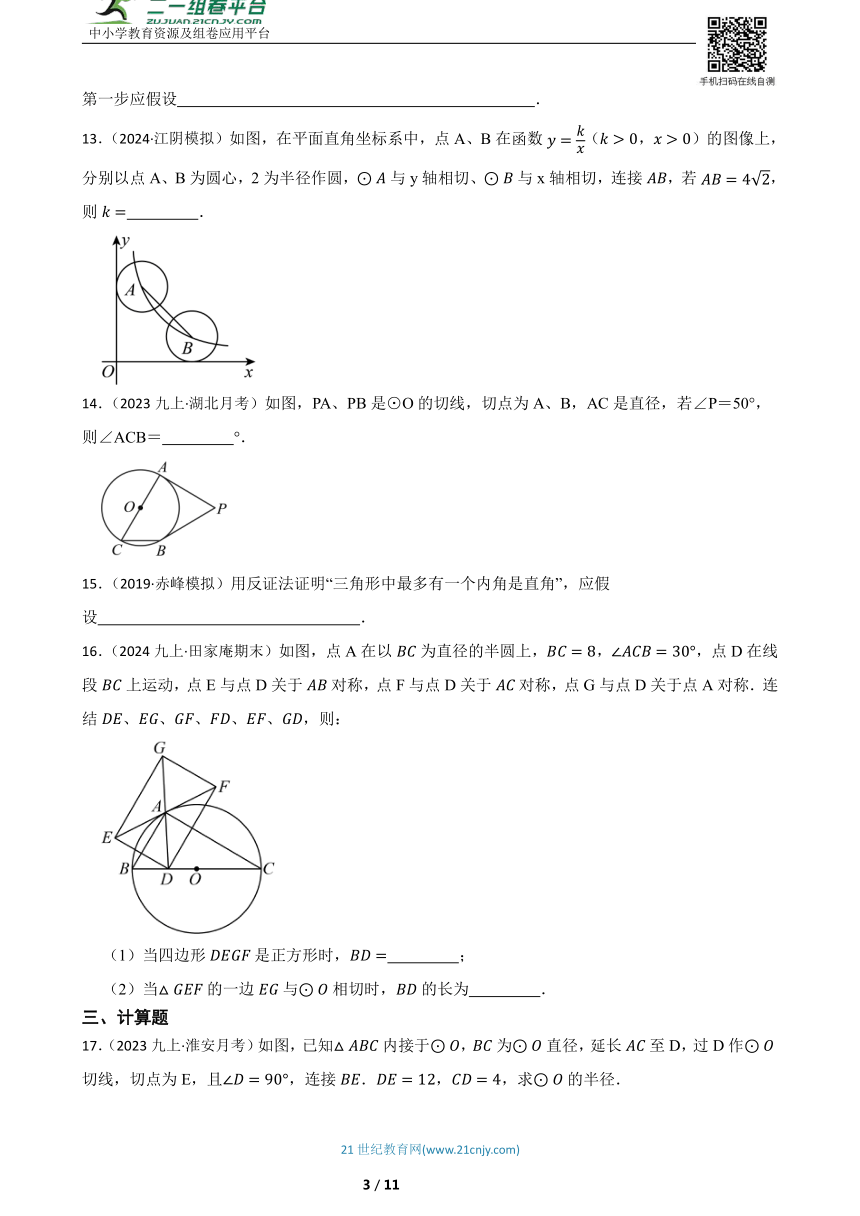
8.(2024九下·南宁模拟)如图,AB是⊙O的直径,C.D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( )
A.40° B.50° C.60° D.70°
9.(2020九上·海曙期末)《九章算术》中有这样一个问题:“今有勾八步,股十五步,问勾中容圆径几何 ”其意思是:“直角三角形中,勾(短直角边)长为8步,股(长直角边)长为15步,求直角三角形能容纳的圆形(内切圆)直径”。则该圆的直径为( )
A.3步 B.5步 C.6步 D.8步
10.(2025九下·荣县期中)在平面直角坐标系中,,双曲线上一点P,以点P为圆心的过两点且与y轴相切,则k的值为( )
A.12 B. C. D.
二、填空题
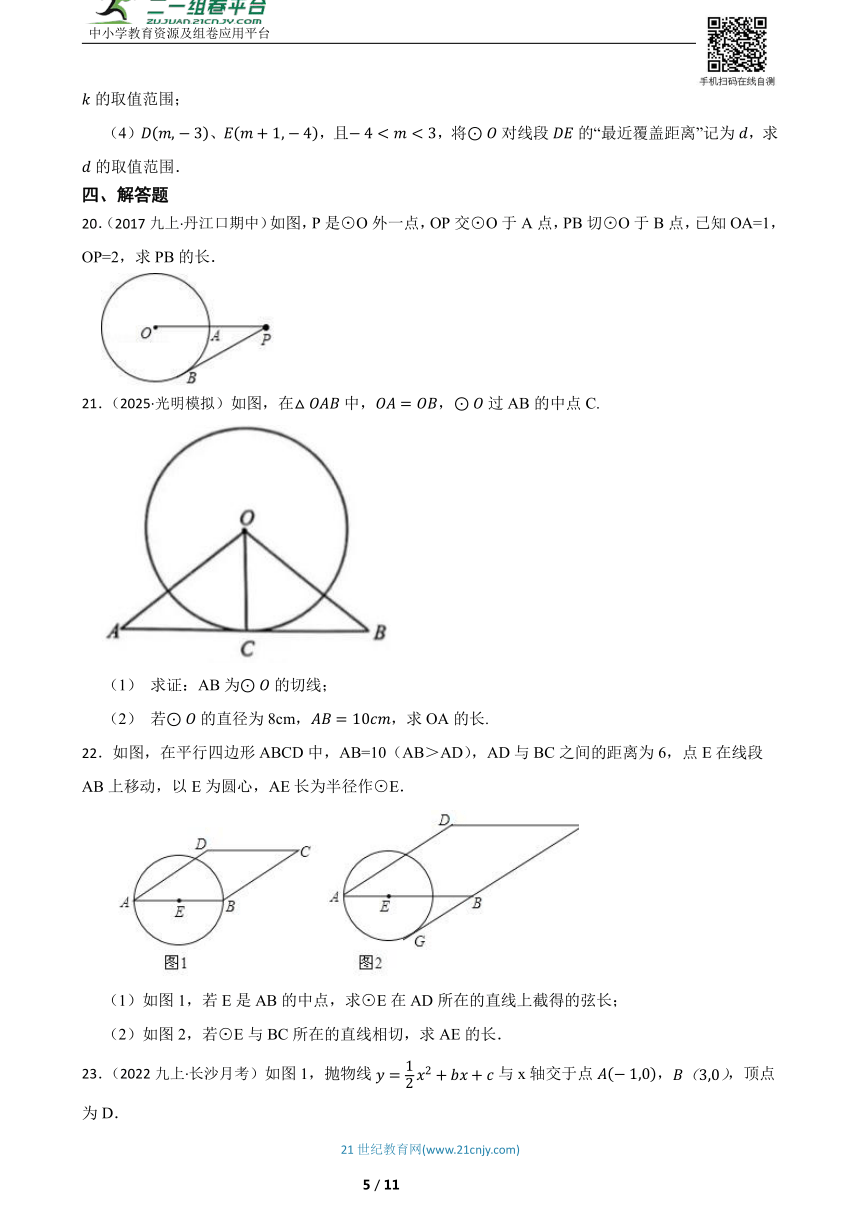
11.(2024九下·滨州模拟)如图,点是外接圆的圆心,点是的内心,连接.若,则的度数为 .
12.(2024八下·邳州期中)用反证法证明命题:“一组对边平行但不相等的四边形不是平行四边形”时,第一步应假设 .
13.(2024·江阴模拟)如图,在平面直角坐标系中,点A、B在函数(,)的图像上,分别以点A、B为圆心,2为半径作圆,与y轴相切、与x轴相切,连接,若,则 .
14.(2023九上·湖北月考)如图,PA、PB是⊙O的切线,切点为A、B,AC是直径,若∠P=50°,则∠ACB= °.
15.(2019·赤峰模拟)用反证法证明“三角形中最多有一个内角是直角”,应假设 .
16.(2024九上·田家庵期末)如图,点A在以为直径的半圆上,,,点D在线段上运动,点E与点D关于对称,点F与点D关于对称,点G与点D关于点A对称.连结、、、、、,则:
(1)当四边形是正方形时, ;
(2)当的一边与相切时,的长为 .
三、计算题
17.(2023九上·淮安月考)如图,已知内接于,为直径,延长至D,过D作切线,切点为E,且,连接.,,求的半径.
18.(2025九上·泸州期末)如图,为的切线,为切点,是上一点,过点作,垂足为,交于点.
(1)如图①,若,求的度数;
(2)如图②,连接并延长交于点,连接,,若,的半径为,求的长.
19.(2024九上·北京市月考)【概念学习】
在平面直角坐标系中,的半径为1,若平移个单位后,使某图形上所有点在内或上,则称的最小值为对该图形的“最近覆盖距离”.例如,如图,,,则对线段的“最近覆盖距离”为3.
【概念理解】
(1)对点的“最近覆盖距离”为______________;
(2)点是函数图像上一点,且对点的“最近覆盖距离”为2,则点的坐标为________________;
【拓展应用】
(3)若一次函数的图像上存在点,使对点的“最近覆盖距离”为,求的取值范围;
(4)、,且,将对线段的“最近覆盖距离”记为,求的取值范围.
四、解答题
20.(2017九上·丹江口期中)如图,P是⊙O外一点,OP交⊙O于A点,PB切⊙O于B点,已知OA=1,OP=2,求PB的长.
21.(2025·光明模拟)如图,在中,,过AB的中点C.
(1) 求证:AB为的切线;
(2) 若的直径为8cm,,求OA的长.
22.如图,在平行四边形ABCD中,AB=10(AB>AD),AD与BC之间的距离为6,点E在线段AB上移动,以E为圆心,AE长为半径作⊙E.
(1)如图1,若E是AB的中点,求⊙E在AD所在的直线上截得的弦长;
(2)如图2,若⊙E与BC所在的直线相切,求AE的长.
23.(2022九上·长沙月考)如图1,抛物线与x轴交于点,,顶点为D.
(1)求抛物线的解析式;
(2)如图2,以为直径在x轴上方画半圆交y轴于点E,圆心为G,连接,点Q为的中点.
①判断点C、D与的位置关系,并说明原因;
②当点P沿半圆从点B运动到点A时,求线段的最小值.
答案解析部分
1.【答案】B
【知识点】确定圆的条件
2.【答案】C
【知识点】反证法
3.【答案】C
【知识点】勾股定理;切线的性质
4.【答案】B
【知识点】直线与圆的位置关系
5.【答案】A
【知识点】点与圆的位置关系
6.【答案】A
【知识点】反证法
7.【答案】C
【知识点】坐标与图形性质;切线的判定
8.【答案】B
【知识点】圆周角定理;切线的性质
9.【答案】C
【知识点】切线的性质;三角形的内切圆与内心
10.【答案】D
【知识点】勾股定理;垂径定理;切线的性质
11.【答案】
【知识点】三角形内角和定理;等腰三角形的性质;圆周角定理;三角形的内切圆与内心
12.【答案】一组对边平行但不相等的四边形是平行四边形
【知识点】反证法
13.【答案】12
【知识点】勾股定理;切线的性质
14.【答案】65
【知识点】切线的性质
15.【答案】三角形中最少有两个内角是直角
【知识点】反证法
16.【答案】;
【知识点】含30°角的直角三角形;圆周角定理;切线的性质;坐标与图形变化﹣对称
17.【答案】半径
【知识点】勾股定理;矩形的判定;切线的性质
18.【答案】(1)
(2)
【知识点】等边三角形的判定与性质;含30°角的直角三角形;圆周角定理;切线的性质
19.【答案】(1)(2)或(3)或(4)
【知识点】等腰三角形的判定与性质;直线与圆的位置关系;一次函数的实际应用-几何问题;等腰三角形的概念
20.【答案】解:连接OB,
∵PB切⊙O于点B,
∴∠B=90°,
∵OA=1,
∴OB=OA=R=1,
∴OP=2,
∴PB= .
【知识点】勾股定理;切线的性质
21.【答案】(1)证明:
经过点C
是的切线.
(2)解:的直径为8cm
在 中,由勾股定理可得
【知识点】勾股定理;切线的判定;等腰三角形的性质-三线合一
22.【答案】解:(1)设AD和圆相交于F,连接BF,
∵AB是圆的直径,
∴∠AFB=90°,
∴BF⊥AD,
∵AD与BC之间的距离为6,
∴BF=6,
∴AB=10,
∴AF==8;
(2)过点B作BM⊥AD于点M,连接EG.
∵AD与BC之间的距离为6,
∴BM=6;
∴sin∠DAB==;
又∵CG是⊙E的切线,
∴EG⊥CG,
∴cos∠BEG=;
∵四边形ABCD是平行四边形,
∴AD∥BC(平行四边形的对边相互平行),
∴∠DAB=∠ABG(两直线平行,内错角相等);
∵AE=EG(⊙E的半径),
∴
即,
∴AE=.
【知识点】切线的性质
23.【答案】(1)解:将,代入,∴,
解得:,所以;
(2)解:①令,则,∴,
因为,
所以,
因为,,
所以,圆的半径为,
因为,,
所以,,
所以C点在圆G的内部,D点在圆上;
②连接并延长与圆交于点N,连接,
所以,
因为G是的中点,Q是的中点,
所以,
所以,
所以Q点在以为圆心,1为半径的圆上,
因为,
所以的最小值为,
所以线段的最小值为.
【知识点】待定系数法求二次函数解析式;勾股定理;点与圆的位置关系
21世纪教育网(www.21cnjy.com)
2 / 11
24.2 点和圆、直线和圆的位置关系本节综合题
一、单选题
1.(2023九上·海宁月考)如图,在的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
A.点P B.点Q C.点R D.点M
2.应用反证法推出矛盾的推导过程中要把下列哪些作为条件使用( )
①结论的否定;②已知条件;③公理、定理、定义等;④原结论.
A.①② B.②③ C.①②③ D.①②④
3.(2023·龙港模拟)如图,与相切于点,若的半径为,,则的长为( )
A. B. C. D.4
4.若⊙O的直径为20cm,点O到直线l的距离为10cm,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法确定
5.(2024九上·遵化期末)已知⊙O的半径为4cm,A为线段OP的中点,当OP=6cm时,点A与⊙O的位置关系是( )
A.A在⊙O内 B.A在⊙O上 C.A在⊙O外 D.不能确定
6.(2023八下·高碑店期中)用反证法证明命题“在中,若,则”,首先应假设( )
A. B. C. D.
7.如图,在直角坐标系中,⊙O的半径为1,则直线y=﹣2x+ 与⊙O的位置关系是( )
A.相离 B.相交 C.相切 D.无法确定
8.(2024九下·南宁模拟)如图,AB是⊙O的直径,C.D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( )
A.40° B.50° C.60° D.70°
9.(2020九上·海曙期末)《九章算术》中有这样一个问题:“今有勾八步,股十五步,问勾中容圆径几何 ”其意思是:“直角三角形中,勾(短直角边)长为8步,股(长直角边)长为15步,求直角三角形能容纳的圆形(内切圆)直径”。则该圆的直径为( )
A.3步 B.5步 C.6步 D.8步
10.(2025九下·荣县期中)在平面直角坐标系中,,双曲线上一点P,以点P为圆心的过两点且与y轴相切,则k的值为( )
A.12 B. C. D.
二、填空题
11.(2024九下·滨州模拟)如图,点是外接圆的圆心,点是的内心,连接.若,则的度数为 .
12.(2024八下·邳州期中)用反证法证明命题:“一组对边平行但不相等的四边形不是平行四边形”时,第一步应假设 .
13.(2024·江阴模拟)如图,在平面直角坐标系中,点A、B在函数(,)的图像上,分别以点A、B为圆心,2为半径作圆,与y轴相切、与x轴相切,连接,若,则 .
14.(2023九上·湖北月考)如图,PA、PB是⊙O的切线,切点为A、B,AC是直径,若∠P=50°,则∠ACB= °.
15.(2019·赤峰模拟)用反证法证明“三角形中最多有一个内角是直角”,应假设 .
16.(2024九上·田家庵期末)如图,点A在以为直径的半圆上,,,点D在线段上运动,点E与点D关于对称,点F与点D关于对称,点G与点D关于点A对称.连结、、、、、,则:
(1)当四边形是正方形时, ;
(2)当的一边与相切时,的长为 .
三、计算题
17.(2023九上·淮安月考)如图,已知内接于,为直径,延长至D,过D作切线,切点为E,且,连接.,,求的半径.
18.(2025九上·泸州期末)如图,为的切线,为切点,是上一点,过点作,垂足为,交于点.
(1)如图①,若,求的度数;
(2)如图②,连接并延长交于点,连接,,若,的半径为,求的长.
19.(2024九上·北京市月考)【概念学习】
在平面直角坐标系中,的半径为1,若平移个单位后,使某图形上所有点在内或上,则称的最小值为对该图形的“最近覆盖距离”.例如,如图,,,则对线段的“最近覆盖距离”为3.
【概念理解】
(1)对点的“最近覆盖距离”为______________;
(2)点是函数图像上一点,且对点的“最近覆盖距离”为2,则点的坐标为________________;
【拓展应用】
(3)若一次函数的图像上存在点,使对点的“最近覆盖距离”为,求的取值范围;
(4)、,且,将对线段的“最近覆盖距离”记为,求的取值范围.
四、解答题
20.(2017九上·丹江口期中)如图,P是⊙O外一点,OP交⊙O于A点,PB切⊙O于B点,已知OA=1,OP=2,求PB的长.
21.(2025·光明模拟)如图,在中,,过AB的中点C.
(1) 求证:AB为的切线;
(2) 若的直径为8cm,,求OA的长.
22.如图,在平行四边形ABCD中,AB=10(AB>AD),AD与BC之间的距离为6,点E在线段AB上移动,以E为圆心,AE长为半径作⊙E.
(1)如图1,若E是AB的中点,求⊙E在AD所在的直线上截得的弦长;
(2)如图2,若⊙E与BC所在的直线相切,求AE的长.
23.(2022九上·长沙月考)如图1,抛物线与x轴交于点,,顶点为D.
(1)求抛物线的解析式;
(2)如图2,以为直径在x轴上方画半圆交y轴于点E,圆心为G,连接,点Q为的中点.
①判断点C、D与的位置关系,并说明原因;
②当点P沿半圆从点B运动到点A时,求线段的最小值.
答案解析部分
1.【答案】B
【知识点】确定圆的条件
2.【答案】C
【知识点】反证法
3.【答案】C
【知识点】勾股定理;切线的性质
4.【答案】B
【知识点】直线与圆的位置关系
5.【答案】A
【知识点】点与圆的位置关系
6.【答案】A
【知识点】反证法
7.【答案】C
【知识点】坐标与图形性质;切线的判定
8.【答案】B
【知识点】圆周角定理;切线的性质
9.【答案】C
【知识点】切线的性质;三角形的内切圆与内心
10.【答案】D
【知识点】勾股定理;垂径定理;切线的性质
11.【答案】
【知识点】三角形内角和定理;等腰三角形的性质;圆周角定理;三角形的内切圆与内心
12.【答案】一组对边平行但不相等的四边形是平行四边形
【知识点】反证法
13.【答案】12
【知识点】勾股定理;切线的性质
14.【答案】65
【知识点】切线的性质
15.【答案】三角形中最少有两个内角是直角
【知识点】反证法
16.【答案】;
【知识点】含30°角的直角三角形;圆周角定理;切线的性质;坐标与图形变化﹣对称
17.【答案】半径
【知识点】勾股定理;矩形的判定;切线的性质
18.【答案】(1)
(2)
【知识点】等边三角形的判定与性质;含30°角的直角三角形;圆周角定理;切线的性质
19.【答案】(1)(2)或(3)或(4)
【知识点】等腰三角形的判定与性质;直线与圆的位置关系;一次函数的实际应用-几何问题;等腰三角形的概念
20.【答案】解:连接OB,
∵PB切⊙O于点B,
∴∠B=90°,
∵OA=1,
∴OB=OA=R=1,
∴OP=2,
∴PB= .
【知识点】勾股定理;切线的性质
21.【答案】(1)证明:
经过点C
是的切线.
(2)解:的直径为8cm
在 中,由勾股定理可得
【知识点】勾股定理;切线的判定;等腰三角形的性质-三线合一
22.【答案】解:(1)设AD和圆相交于F,连接BF,
∵AB是圆的直径,
∴∠AFB=90°,
∴BF⊥AD,
∵AD与BC之间的距离为6,
∴BF=6,
∴AB=10,
∴AF==8;
(2)过点B作BM⊥AD于点M,连接EG.
∵AD与BC之间的距离为6,
∴BM=6;
∴sin∠DAB==;
又∵CG是⊙E的切线,
∴EG⊥CG,
∴cos∠BEG=;
∵四边形ABCD是平行四边形,
∴AD∥BC(平行四边形的对边相互平行),
∴∠DAB=∠ABG(两直线平行,内错角相等);
∵AE=EG(⊙E的半径),
∴
即,
∴AE=.
【知识点】切线的性质
23.【答案】(1)解:将,代入,∴,
解得:,所以;
(2)解:①令,则,∴,
因为,
所以,
因为,,
所以,圆的半径为,
因为,,
所以,,
所以C点在圆G的内部,D点在圆上;
②连接并延长与圆交于点N,连接,
所以,
因为G是的中点,Q是的中点,
所以,
所以,
所以Q点在以为圆心,1为半径的圆上,
因为,
所以的最小值为,
所以线段的最小值为.
【知识点】待定系数法求二次函数解析式;勾股定理;点与圆的位置关系
21世纪教育网(www.21cnjy.com)
2 / 11
同课章节目录
