24.3 正多边形和圆 同步练习(含答案)
文档属性
| 名称 | 24.3 正多边形和圆 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 458.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-09 10:53:39 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
24.3 正多边形和圆
一、单选题
1.(2022·平谷模拟)如图,四边形ABCD内接于⊙O,∠D=110°,则∠AOC的度数是( )
A.55° B.110° C.130° D.140°
2.如图①是我国古建筑墙上采用的八角形空窗, 其轮廓是一个正八边形, 窗外之境如同镶嵌于一个画框之中. 如图②是八角形空窗的示意图, 它的一个外角 ( )
A. B. C.. D.
3.正多边形的中心角是36°,那么这个正多边形的边数是( )
A.10 B.8 C.6 D.5
4.(2022九上·香洲期末)圆的内接正多边形中,正多边形的一条边所对的圆心角是,则正多边形的边数是( )
A.4 B.5 C.6 D.8
5.(2024九下·渠县月考)正六边形的半径为,则它的边心距是( )
A. B. C. D.
6.(2024八下·石阡月考)已知一个正n边形的一个外角为,则n=( )
A.10 B.9 C.8 D.7
7.(2018·桐乡模拟)如图,四边形OBCD中,若 则 等于( )
A. B. C. D.
8.(2024九下·霍邱月考)如图,圆内接正九边形两条对角线相交,则的度数是( )
A. B. C. D.
9.(2024九上·兰溪期中)如图,正六边形与正方形有两个顶点重合,且中心都是点O.若是某正n边形的一个外角,则n的值为( )
A.16 B.12 C.10 D.8
10.(2022九下·黄石模拟)如图是由三个大小相同的正方形组成的“品”字型轴对称图案,测得顶点A,B之间的距离为5.现用一个半径为r的圆形纸片将其完全覆盖,则r的最小值是( )
A. B. C. D.
二、填空题
11.(2021九上·拱墅期中)已知一个正多边形内角的度数为108°,则它的边数为 .
12.(2024九下·建邺模拟)边长为2的正六边形的面积为 .
13.(2023九上·句容期中)如图所示,四边形ABCD内接于,如果它的一个外角∠DCE=65°,那么∠BOD等于 .
14.已知正六边形ABCDEF的边心距为cm,则正六边形的半径为 cm.
15.(2024·临夏)“香渡栏干屈曲,红妆映、薄绮疏棂.”图1窗棂的外边框为正六边形(如图2),则该正六边形的每个内角为 .
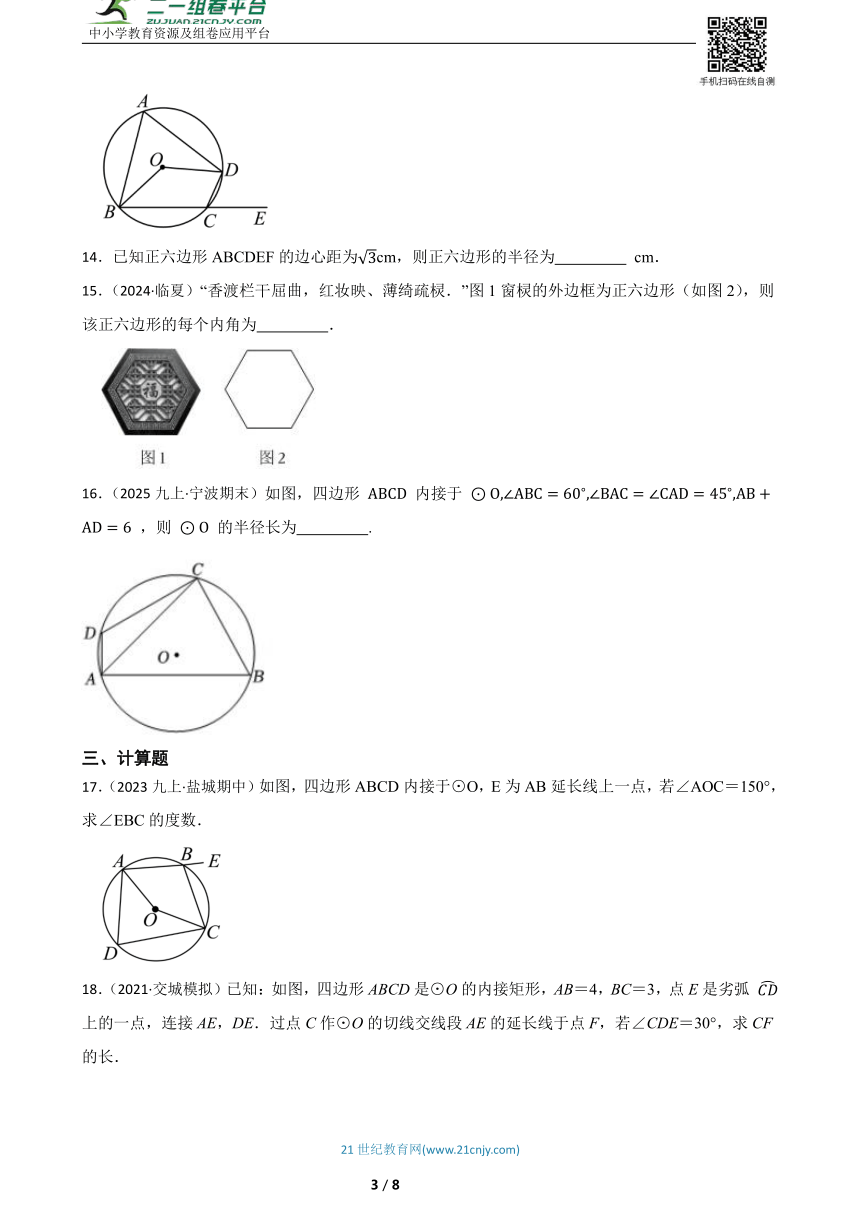
16.(2025九上·宁波期末)如图,四边形 内接于 ,则 的半径长为 .
三、计算题
17.(2023九上·盐城期中)如图,四边形ABCD内接于⊙O,E为AB延长线上一点,若∠AOC=150°,求∠EBC的度数.
18.(2021·交城模拟)已知:如图,四边形ABCD是⊙O的内接矩形,AB=4,BC=3,点E是劣弧 上的一点,连接AE,DE.过点C作⊙O的切线交线段AE的延长线于点F,若∠CDE=30°,求CF的长.
四、解答题
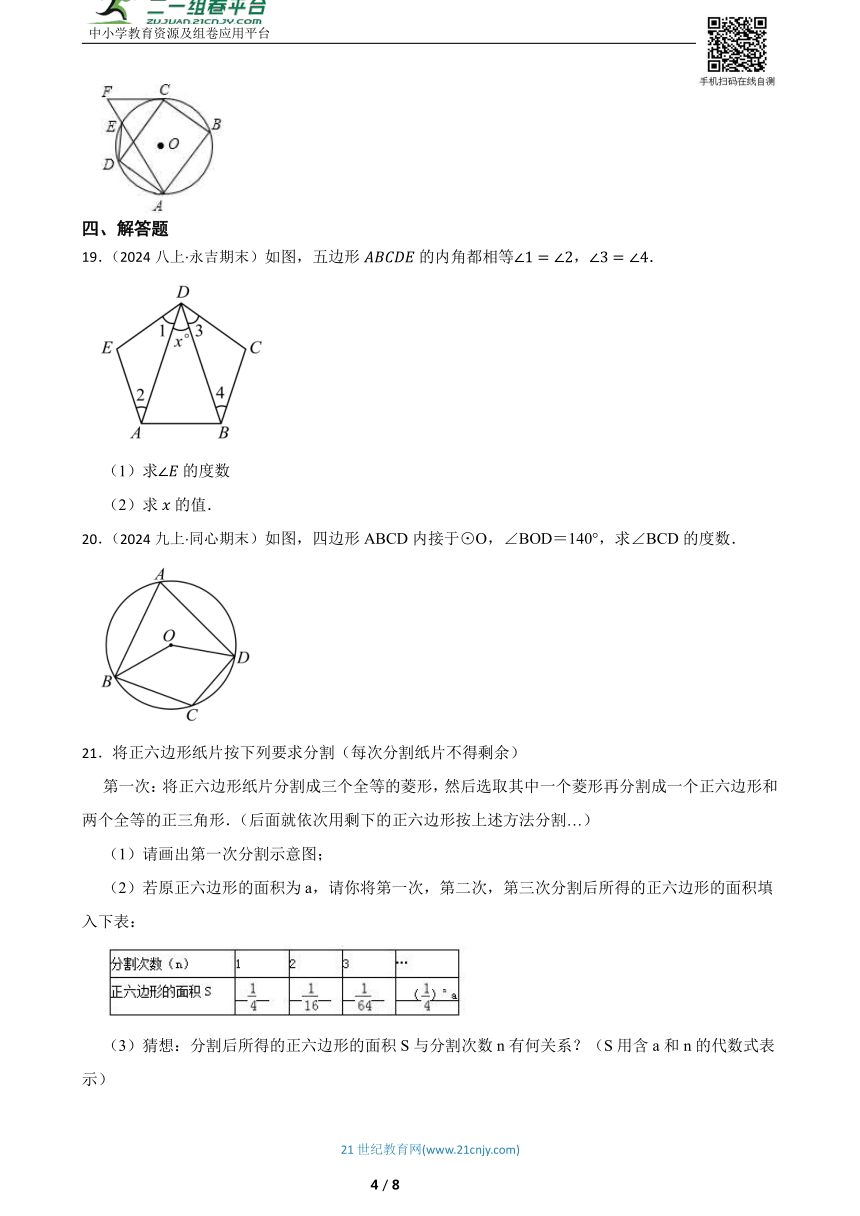
19.(2024八上·永吉期末)如图,五边形的内角都相等,.
(1)求的度数
(2)求的值.
20.(2024九上·同心期末)如图,四边形ABCD内接于⊙O,∠BOD=140°,求∠BCD的度数.
21.将正六边形纸片按下列要求分割(每次分割纸片不得剩余)
第一次:将正六边形纸片分割成三个全等的菱形,然后选取其中一个菱形再分割成一个正六边形和两个全等的正三角形.(后面就依次用剩下的正六边形按上述方法分割…)
(1)请画出第一次分割示意图;
(2)若原正六边形的面积为a,请你将第一次,第二次,第三次分割后所得的正六边形的面积填入下表:
(3)猜想:分割后所得的正六边形的面积S与分割次数n有何关系?(S用含a和n的代数式表示)
22.(2024九上·江北开学考)如图正方形内接于,为任意一点,连接、.
(1)求的度数.
(2)如图2,过点作交于点,连接,,,,求的长度.
答案解析部分
1.【答案】D
【知识点】圆周角定理;圆内接四边形的性质
2.【答案】A
【知识点】正多边形的性质;多边形的外角和公式
3.【答案】A
【知识点】圆内接正多边形
4.【答案】B
【知识点】圆内接正多边形
5.【答案】C
【知识点】圆内接正多边形
6.【答案】B
【知识点】多边形内角与外角;正多边形的性质
7.【答案】C
【知识点】圆周角定理;圆内接四边形的性质
8.【答案】C
【知识点】三角形的外角性质;圆周角定理;圆内接正多边形
9.【答案】B
【知识点】圆内接正多边形
10.【答案】B
【知识点】勾股定理;圆内接正多边形
11.【答案】5
【知识点】正多边形的性质
12.【答案】
【知识点】等边三角形的判定与性质;圆内接正多边形
13.【答案】130°
【知识点】圆周角定理;圆内接四边形的性质
14.【答案】2
【知识点】圆内接正多边形
15.【答案】120°
【知识点】正多边形的性质;多边形的内角和公式
16.【答案】
【知识点】含30°角的直角三角形;勾股定理;圆内接四边形的性质;三角形全等的判定-AAS
17.【答案】
【知识点】圆周角定理;圆内接四边形的性质
18.【答案】解:连接AC,如图,
∵四边形ABCD是⊙O的内接矩形,
∴∠ABC=90°,AC= ,
∴AC为⊙O的直径,
∵CF为切线,
∴AC⊥CF,
∵∠CAE=∠CDE=30°,
∴CF= AC= .
【知识点】含30°角的直角三角形;圆内接四边形的性质;切线的性质
19.【答案】(1)解:∵五边形的内角都相等,
∴.
(2)解:由(1)可知,
∵,
∴,
同理可得:,
∴,
∴.
【知识点】三角形内角和定理;多边形内角与外角;正多边形的性质
20.【答案】110°
【知识点】圆周角定理;圆内接四边形的性质
21.【答案】解:
;
(2)S1=a S2=a S3=a;
(3)Sn=()n a.
【知识点】圆内接正多边形
22.【答案】(1)
(2)
【知识点】勾股定理;圆内接正多边形
21世纪教育网(www.21cnjy.com)
1 / 8
24.3 正多边形和圆
一、单选题
1.(2022·平谷模拟)如图,四边形ABCD内接于⊙O,∠D=110°,则∠AOC的度数是( )
A.55° B.110° C.130° D.140°
2.如图①是我国古建筑墙上采用的八角形空窗, 其轮廓是一个正八边形, 窗外之境如同镶嵌于一个画框之中. 如图②是八角形空窗的示意图, 它的一个外角 ( )
A. B. C.. D.
3.正多边形的中心角是36°,那么这个正多边形的边数是( )
A.10 B.8 C.6 D.5
4.(2022九上·香洲期末)圆的内接正多边形中,正多边形的一条边所对的圆心角是,则正多边形的边数是( )
A.4 B.5 C.6 D.8
5.(2024九下·渠县月考)正六边形的半径为,则它的边心距是( )
A. B. C. D.
6.(2024八下·石阡月考)已知一个正n边形的一个外角为,则n=( )
A.10 B.9 C.8 D.7
7.(2018·桐乡模拟)如图,四边形OBCD中,若 则 等于( )
A. B. C. D.
8.(2024九下·霍邱月考)如图,圆内接正九边形两条对角线相交,则的度数是( )
A. B. C. D.
9.(2024九上·兰溪期中)如图,正六边形与正方形有两个顶点重合,且中心都是点O.若是某正n边形的一个外角,则n的值为( )
A.16 B.12 C.10 D.8
10.(2022九下·黄石模拟)如图是由三个大小相同的正方形组成的“品”字型轴对称图案,测得顶点A,B之间的距离为5.现用一个半径为r的圆形纸片将其完全覆盖,则r的最小值是( )
A. B. C. D.
二、填空题
11.(2021九上·拱墅期中)已知一个正多边形内角的度数为108°,则它的边数为 .
12.(2024九下·建邺模拟)边长为2的正六边形的面积为 .
13.(2023九上·句容期中)如图所示,四边形ABCD内接于,如果它的一个外角∠DCE=65°,那么∠BOD等于 .
14.已知正六边形ABCDEF的边心距为cm,则正六边形的半径为 cm.
15.(2024·临夏)“香渡栏干屈曲,红妆映、薄绮疏棂.”图1窗棂的外边框为正六边形(如图2),则该正六边形的每个内角为 .
16.(2025九上·宁波期末)如图,四边形 内接于 ,则 的半径长为 .
三、计算题
17.(2023九上·盐城期中)如图,四边形ABCD内接于⊙O,E为AB延长线上一点,若∠AOC=150°,求∠EBC的度数.
18.(2021·交城模拟)已知:如图,四边形ABCD是⊙O的内接矩形,AB=4,BC=3,点E是劣弧 上的一点,连接AE,DE.过点C作⊙O的切线交线段AE的延长线于点F,若∠CDE=30°,求CF的长.
四、解答题
19.(2024八上·永吉期末)如图,五边形的内角都相等,.
(1)求的度数
(2)求的值.
20.(2024九上·同心期末)如图,四边形ABCD内接于⊙O,∠BOD=140°,求∠BCD的度数.
21.将正六边形纸片按下列要求分割(每次分割纸片不得剩余)
第一次:将正六边形纸片分割成三个全等的菱形,然后选取其中一个菱形再分割成一个正六边形和两个全等的正三角形.(后面就依次用剩下的正六边形按上述方法分割…)
(1)请画出第一次分割示意图;
(2)若原正六边形的面积为a,请你将第一次,第二次,第三次分割后所得的正六边形的面积填入下表:
(3)猜想:分割后所得的正六边形的面积S与分割次数n有何关系?(S用含a和n的代数式表示)
22.(2024九上·江北开学考)如图正方形内接于,为任意一点,连接、.
(1)求的度数.
(2)如图2,过点作交于点,连接,,,,求的长度.
答案解析部分
1.【答案】D
【知识点】圆周角定理;圆内接四边形的性质
2.【答案】A
【知识点】正多边形的性质;多边形的外角和公式
3.【答案】A
【知识点】圆内接正多边形
4.【答案】B
【知识点】圆内接正多边形
5.【答案】C
【知识点】圆内接正多边形
6.【答案】B
【知识点】多边形内角与外角;正多边形的性质
7.【答案】C
【知识点】圆周角定理;圆内接四边形的性质
8.【答案】C
【知识点】三角形的外角性质;圆周角定理;圆内接正多边形
9.【答案】B
【知识点】圆内接正多边形
10.【答案】B
【知识点】勾股定理;圆内接正多边形
11.【答案】5
【知识点】正多边形的性质
12.【答案】
【知识点】等边三角形的判定与性质;圆内接正多边形
13.【答案】130°
【知识点】圆周角定理;圆内接四边形的性质
14.【答案】2
【知识点】圆内接正多边形
15.【答案】120°
【知识点】正多边形的性质;多边形的内角和公式
16.【答案】
【知识点】含30°角的直角三角形;勾股定理;圆内接四边形的性质;三角形全等的判定-AAS
17.【答案】
【知识点】圆周角定理;圆内接四边形的性质
18.【答案】解:连接AC,如图,
∵四边形ABCD是⊙O的内接矩形,
∴∠ABC=90°,AC= ,
∴AC为⊙O的直径,
∵CF为切线,
∴AC⊥CF,
∵∠CAE=∠CDE=30°,
∴CF= AC= .
【知识点】含30°角的直角三角形;圆内接四边形的性质;切线的性质
19.【答案】(1)解:∵五边形的内角都相等,
∴.
(2)解:由(1)可知,
∵,
∴,
同理可得:,
∴,
∴.
【知识点】三角形内角和定理;多边形内角与外角;正多边形的性质
20.【答案】110°
【知识点】圆周角定理;圆内接四边形的性质
21.【答案】解:
;
(2)S1=a S2=a S3=a;
(3)Sn=()n a.
【知识点】圆内接正多边形
22.【答案】(1)
(2)
【知识点】勾股定理;圆内接正多边形
21世纪教育网(www.21cnjy.com)
1 / 8
同课章节目录
