24.4 弧长及扇形的面积 同步练习(含答案)
文档属性
| 名称 | 24.4 弧长及扇形的面积 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 818.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-09 10:55:05 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
24.4 弧长及扇形的面积
一、单选题
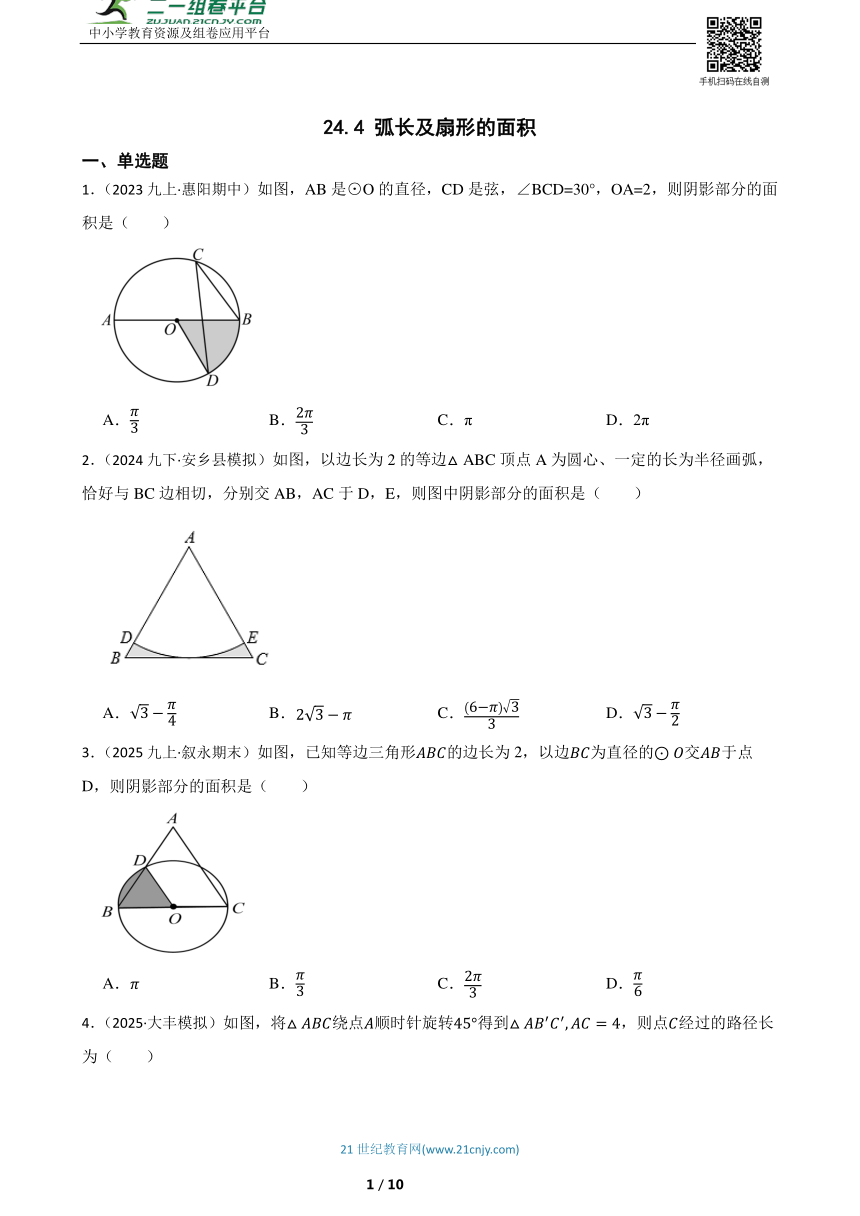
1.(2023九上·惠阳期中)如图,AB是⊙O的直径,CD是弦,∠BCD=30°,OA=2,则阴影部分的面积是( )
A. B. C.π D.2π
2.(2024九下·安乡县模拟)如图,以边长为2的等边△ABC顶点A为圆心、一定的长为半径画弧,恰好与BC边相切,分别交AB,AC于D,E,则图中阴影部分的面积是( )
A. B. C. D.
3.(2025九上·叙永期末)如图,已知等边三角形的边长为2,以边为直径的交于点D,则阴影部分的面积是( )
A. B. C. D.
4.(2025·大丰模拟)如图,将绕点顺时针旋转得到,则点经过的路径长为( )
A. B. C. D.
5.(2024九上·西湖月考)如图,是的内接三角形,,,连接、,则弧的长是( )
A. B. C. D.
6.一个扇形的圆心角是120°,它的面积为3πcm2,那么这个扇形的半径是( )
A.cm B.3cm C.6cm D.9cm
7.(2021九上·南宁期末)如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A,B,与⊙O1分别交于C,D,则 与 的弧长之和为( )
A. B. C. D.
8.如图,在Rt△ABC中,∠ABC=40°,AB=6,斜边AB是半圆O的直径,点D是半圆上的一个动点,连结CD与AB交于点E,若△BCE是等腰三角形,则的长为( )
A.π B.π或π C.π或π D.π或π
9.如图是一个圆形的街心花园,A、B、C是圆周上的三个娱乐点,且A、B、C三等分圆周,街心花园内除了沿圆周的一条主要道路外还有经过圆心的, , 三条道路,一天早晨,有甲、乙两位晨练者同时从A点出发,其中甲沿着圆走回原处A,乙沿着 , , 也走回原处,假设他们行走的速度相同,则下列结论正确的是( ).
A.甲先回到A B.乙先回到A C.同时回到A D.无法确定
10.(2019·沈丘模拟)如图,在矩形ABCD中AB= ,BC=1,将矩形ABCD绕顶点B旋转得到矩形A'BC'D,点A恰好落在矩形ABCD的边CD上,则AD扫过的部分(即阴影部分)面积为( )
A. B. C. D.
二、填空题
11.(2024九下·桐柏模拟)图,等腰直角三角形中,,,为上一点,,以为圆心,为半径画弧交于点,交的延长线于点,则图中阴影部分面积为 .
12.(2023·香坊模拟)某扇形的圆心角是45°,面积为 ,该扇形的半径是 .
13.(2024九上·雨花台期中)已知扇形的圆心角为,半径是,则扇形的面积为 .
14.抖空竹在我国有着悠久的历史,是国家级非物质文化遗产之一.如图,AC,BD 分别与⊙O相切于点C,D,延长AC,BD相交于点P.若∠P=120° ⊙O 的半径为 6cm,则图中CD的长为 cm.(结果保留π)
15.(2016·贵港)如图,在Rt△ABC中,∠C=90°,∠BAC=60°,将△ABC绕点A逆时针旋转60°后得到△ADE,若AC=1,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 (结果保留π).
16.(2021·姑苏模拟)一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘,如图所示,AB与CD水平,BC与水平面的夹角为60°,其中AB=60cm,CD=40cm,BC=40cm,那么该小朋友将圆盘从A点滚动到D点其圆心所经过的路线长为 cm.
三、计算题
17.(2023九上·昭阳月考)如图,在中,,,,若以点为圆心,长为半径的弧交于点,以为圆心,长为半径的弧交于点,求图中阴影部分图形的面积.
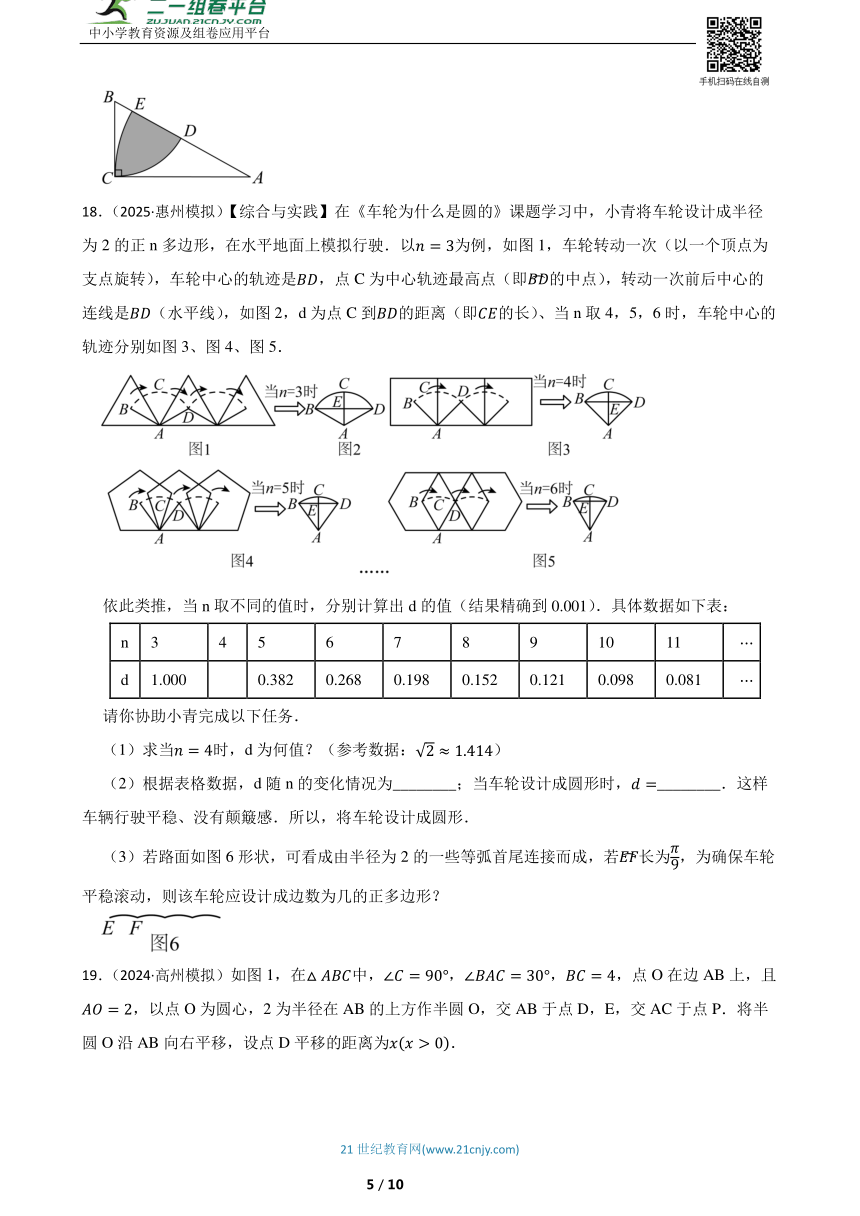
18.(2025·惠州模拟)【综合与实践】在《车轮为什么是圆的》课题学习中,小青将车轮设计成半径为2的正n多边形,在水平地面上模拟行驶.以为例,如图1,车轮转动一次(以一个顶点为支点旋转),车轮中心的轨迹是,点C为中心轨迹最高点(即的中点),转动一次前后中心的连线是(水平线),如图2,d为点C到的距离(即的长)、当n取4,5,6时,车轮中心的轨迹分别如图3、图4、图5.
依此类推,当n取不同的值时,分别计算出d的值(结果精确到0.001).具体数据如下表:
n 3 4 5 6 7 8 9 10 11
d 1.000 0.382 0.268 0.198 0.152 0.121 0.098 0.081
请你协助小青完成以下任务.
(1)求当时,d为何值?(参考数据:)
(2)根据表格数据,d随n的变化情况为________;当车轮设计成圆形时,________.这样车辆行驶平稳、没有颠簸感.所以,将车轮设计成圆形.
(3)若路面如图6形状,可看成由半径为2的一些等弧首尾连接而成,若长为,为确保车轮平稳滚动,则该车轮应设计成边数为几的正多边形?
19.(2024·高州模拟)如图1,在中,,,,点O在边AB上,且,以点O为圆心,2为半径在AB的上方作半圆O,交AB于点D,E,交AC于点P.将半圆O沿AB向右平移,设点D平移的距离为.
(1)在图1中,劣弧的长为________;
(2)当半圆O平移到与边AC相切时,如图2所示.
①求x的值;
②已知M,N分别是边BC与上的动点,连接MN,求MN的最小值和最大值之和;
(3)在半圆O沿边AB向右平移的过程中,当半圆O与的重叠部分是半圆O时,直接写出x的取值范围.
四、解答题
20.(2024九上·新余月考)如图,点D在⊙O的直径的延长线上,与相切于点C.若的半径为1,求阴影部分的面积.
21.(2024九下·阎良开学考)如图,为的直径,是上的一点,连接,若,求的长.(结果保留)
22.(2019九上·延安期中)如图,AB是圆O的直径,AC切圆O于点A,BC交圆O于点D,已知圆O的半径为6, =40°,求弧AD的长.(结果保留 )
23.(2024七下·成都开学考)(组合图形求面积)如图是平行四边形,,,,高,弧、分别以、为半径,弧、分别以、为半径,阴影部分的面积为多少?(取)
答案解析部分
1.【答案】B
【知识点】扇形面积的计算
2.【答案】D
【知识点】等边三角形的性质;勾股定理;扇形面积的计算
3.【答案】D
【知识点】等边三角形的判定与性质;扇形面积的计算
4.【答案】A
【知识点】弧长的计算;旋转的性质
5.【答案】C
【知识点】圆周角定理;圆内接四边形的性质;弧长的计算
6.【答案】B
【知识点】扇形面积的计算
7.【答案】A
【知识点】切线的性质;弧长的计算
8.【答案】C
【知识点】等腰三角形的性质;弧长的计算
9.【答案】C
【知识点】弧长的计算
10.【答案】A
【知识点】三角形的面积;矩形的性质;扇形面积的计算;旋转的性质
11.【答案】
【知识点】勾股定理;扇形面积的计算
12.【答案】12
【知识点】扇形面积的计算
13.【答案】
【知识点】扇形面积的计算
14.【答案】2π
【知识点】切线的性质;弧长的计算;多边形的内角和公式
15.【答案】
【知识点】扇形面积的计算;旋转的性质
16.【答案】
【知识点】平行线的性质;三角形全等及其性质;矩形的性质;弧长的计算
17.【答案】
【知识点】含30°角的直角三角形;勾股定理;扇形面积的计算
18.【答案】(1)0.586
(2)d随n的增大而减小;0
(3)36
【知识点】勾股定理;正方形的性质;弧长的计算
19.【答案】(1)
(2)①;②MN的最小值和最大值之和为
(3)半圆O与的重叠部分是半圆O时,x的取值范围是
【知识点】含30°角的直角三角形;勾股定理;切线的性质;弧长的计算
20.【答案】
【知识点】切线的性质;扇形面积的计算
21.【答案】解:,
,
,
的长.
【知识点】弧长的计算
22.【答案】解:连接OD,
∵AC是⊙O的切线,
∴∠BAC=90°,
∵∠C=40°,
∴∠B=50°,
由圆周角定理得,∠AOD=2∠B=100°,
∴弧AD的长= =
【知识点】圆周角定理;切线的性质;弧长的计算
23.【答案】
【知识点】扇形面积的计算
21世纪教育网(www.21cnjy.com)
2 / 10
24.4 弧长及扇形的面积
一、单选题
1.(2023九上·惠阳期中)如图,AB是⊙O的直径,CD是弦,∠BCD=30°,OA=2,则阴影部分的面积是( )
A. B. C.π D.2π
2.(2024九下·安乡县模拟)如图,以边长为2的等边△ABC顶点A为圆心、一定的长为半径画弧,恰好与BC边相切,分别交AB,AC于D,E,则图中阴影部分的面积是( )
A. B. C. D.
3.(2025九上·叙永期末)如图,已知等边三角形的边长为2,以边为直径的交于点D,则阴影部分的面积是( )
A. B. C. D.
4.(2025·大丰模拟)如图,将绕点顺时针旋转得到,则点经过的路径长为( )
A. B. C. D.
5.(2024九上·西湖月考)如图,是的内接三角形,,,连接、,则弧的长是( )
A. B. C. D.
6.一个扇形的圆心角是120°,它的面积为3πcm2,那么这个扇形的半径是( )
A.cm B.3cm C.6cm D.9cm
7.(2021九上·南宁期末)如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A,B,与⊙O1分别交于C,D,则 与 的弧长之和为( )
A. B. C. D.
8.如图,在Rt△ABC中,∠ABC=40°,AB=6,斜边AB是半圆O的直径,点D是半圆上的一个动点,连结CD与AB交于点E,若△BCE是等腰三角形,则的长为( )
A.π B.π或π C.π或π D.π或π
9.如图是一个圆形的街心花园,A、B、C是圆周上的三个娱乐点,且A、B、C三等分圆周,街心花园内除了沿圆周的一条主要道路外还有经过圆心的, , 三条道路,一天早晨,有甲、乙两位晨练者同时从A点出发,其中甲沿着圆走回原处A,乙沿着 , , 也走回原处,假设他们行走的速度相同,则下列结论正确的是( ).
A.甲先回到A B.乙先回到A C.同时回到A D.无法确定
10.(2019·沈丘模拟)如图,在矩形ABCD中AB= ,BC=1,将矩形ABCD绕顶点B旋转得到矩形A'BC'D,点A恰好落在矩形ABCD的边CD上,则AD扫过的部分(即阴影部分)面积为( )
A. B. C. D.
二、填空题
11.(2024九下·桐柏模拟)图,等腰直角三角形中,,,为上一点,,以为圆心,为半径画弧交于点,交的延长线于点,则图中阴影部分面积为 .
12.(2023·香坊模拟)某扇形的圆心角是45°,面积为 ,该扇形的半径是 .
13.(2024九上·雨花台期中)已知扇形的圆心角为,半径是,则扇形的面积为 .
14.抖空竹在我国有着悠久的历史,是国家级非物质文化遗产之一.如图,AC,BD 分别与⊙O相切于点C,D,延长AC,BD相交于点P.若∠P=120° ⊙O 的半径为 6cm,则图中CD的长为 cm.(结果保留π)
15.(2016·贵港)如图,在Rt△ABC中,∠C=90°,∠BAC=60°,将△ABC绕点A逆时针旋转60°后得到△ADE,若AC=1,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 (结果保留π).
16.(2021·姑苏模拟)一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘,如图所示,AB与CD水平,BC与水平面的夹角为60°,其中AB=60cm,CD=40cm,BC=40cm,那么该小朋友将圆盘从A点滚动到D点其圆心所经过的路线长为 cm.
三、计算题
17.(2023九上·昭阳月考)如图,在中,,,,若以点为圆心,长为半径的弧交于点,以为圆心,长为半径的弧交于点,求图中阴影部分图形的面积.
18.(2025·惠州模拟)【综合与实践】在《车轮为什么是圆的》课题学习中,小青将车轮设计成半径为2的正n多边形,在水平地面上模拟行驶.以为例,如图1,车轮转动一次(以一个顶点为支点旋转),车轮中心的轨迹是,点C为中心轨迹最高点(即的中点),转动一次前后中心的连线是(水平线),如图2,d为点C到的距离(即的长)、当n取4,5,6时,车轮中心的轨迹分别如图3、图4、图5.
依此类推,当n取不同的值时,分别计算出d的值(结果精确到0.001).具体数据如下表:
n 3 4 5 6 7 8 9 10 11
d 1.000 0.382 0.268 0.198 0.152 0.121 0.098 0.081
请你协助小青完成以下任务.
(1)求当时,d为何值?(参考数据:)
(2)根据表格数据,d随n的变化情况为________;当车轮设计成圆形时,________.这样车辆行驶平稳、没有颠簸感.所以,将车轮设计成圆形.
(3)若路面如图6形状,可看成由半径为2的一些等弧首尾连接而成,若长为,为确保车轮平稳滚动,则该车轮应设计成边数为几的正多边形?
19.(2024·高州模拟)如图1,在中,,,,点O在边AB上,且,以点O为圆心,2为半径在AB的上方作半圆O,交AB于点D,E,交AC于点P.将半圆O沿AB向右平移,设点D平移的距离为.
(1)在图1中,劣弧的长为________;
(2)当半圆O平移到与边AC相切时,如图2所示.
①求x的值;
②已知M,N分别是边BC与上的动点,连接MN,求MN的最小值和最大值之和;
(3)在半圆O沿边AB向右平移的过程中,当半圆O与的重叠部分是半圆O时,直接写出x的取值范围.
四、解答题
20.(2024九上·新余月考)如图,点D在⊙O的直径的延长线上,与相切于点C.若的半径为1,求阴影部分的面积.
21.(2024九下·阎良开学考)如图,为的直径,是上的一点,连接,若,求的长.(结果保留)
22.(2019九上·延安期中)如图,AB是圆O的直径,AC切圆O于点A,BC交圆O于点D,已知圆O的半径为6, =40°,求弧AD的长.(结果保留 )
23.(2024七下·成都开学考)(组合图形求面积)如图是平行四边形,,,,高,弧、分别以、为半径,弧、分别以、为半径,阴影部分的面积为多少?(取)
答案解析部分
1.【答案】B
【知识点】扇形面积的计算
2.【答案】D
【知识点】等边三角形的性质;勾股定理;扇形面积的计算
3.【答案】D
【知识点】等边三角形的判定与性质;扇形面积的计算
4.【答案】A
【知识点】弧长的计算;旋转的性质
5.【答案】C
【知识点】圆周角定理;圆内接四边形的性质;弧长的计算
6.【答案】B
【知识点】扇形面积的计算
7.【答案】A
【知识点】切线的性质;弧长的计算
8.【答案】C
【知识点】等腰三角形的性质;弧长的计算
9.【答案】C
【知识点】弧长的计算
10.【答案】A
【知识点】三角形的面积;矩形的性质;扇形面积的计算;旋转的性质
11.【答案】
【知识点】勾股定理;扇形面积的计算
12.【答案】12
【知识点】扇形面积的计算
13.【答案】
【知识点】扇形面积的计算
14.【答案】2π
【知识点】切线的性质;弧长的计算;多边形的内角和公式
15.【答案】
【知识点】扇形面积的计算;旋转的性质
16.【答案】
【知识点】平行线的性质;三角形全等及其性质;矩形的性质;弧长的计算
17.【答案】
【知识点】含30°角的直角三角形;勾股定理;扇形面积的计算
18.【答案】(1)0.586
(2)d随n的增大而减小;0
(3)36
【知识点】勾股定理;正方形的性质;弧长的计算
19.【答案】(1)
(2)①;②MN的最小值和最大值之和为
(3)半圆O与的重叠部分是半圆O时,x的取值范围是
【知识点】含30°角的直角三角形;勾股定理;切线的性质;弧长的计算
20.【答案】
【知识点】切线的性质;扇形面积的计算
21.【答案】解:,
,
,
的长.
【知识点】弧长的计算
22.【答案】解:连接OD,
∵AC是⊙O的切线,
∴∠BAC=90°,
∵∠C=40°,
∴∠B=50°,
由圆周角定理得,∠AOD=2∠B=100°,
∴弧AD的长= =
【知识点】圆周角定理;切线的性质;弧长的计算
23.【答案】
【知识点】扇形面积的计算
21世纪教育网(www.21cnjy.com)
2 / 10
同课章节目录
