13.2.1 三角形的边 课件(共33张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 13.2.1 三角形的边 课件(共33张PPT) 2025-2026学年数学人教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 00:00:00 | ||
图片预览








文档简介
(共33张PPT)
第13章 三角形
13.2 与三角形有关的线段
13.2.1 三角形的边
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
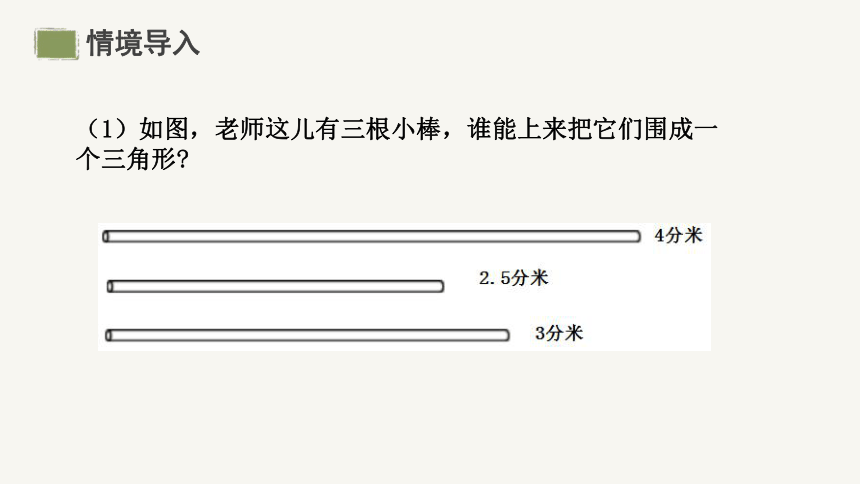
(1)如图,老师这儿有三根小棒,谁能上来把它们围成一个三角形
(2)如图,换三根小棒,谁能上来把它们围成一个三角形
思考:
(2)你能得到什么结论?
(1)为什么有时三根木棒能围成三角形,有时三根木棒不能围成三角形?
新知初探
贰
新知初探
任务一 探究三角形的三边关系
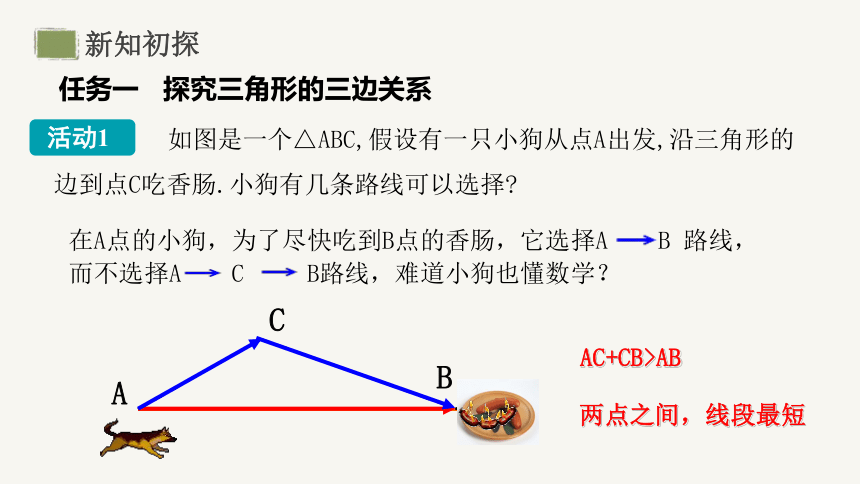
如图是一个△ABC,假设有一只小狗从点A出发,沿三角形的边到点C吃香肠.小狗有几条路线可以选择
在A点的小狗,为了尽快吃到B点的香肠,它选择A B 路线,而不选择A C B路线,难道小狗也懂数学?
C
B
A
AC+CB>AB
两点之间,线段最短
活动1
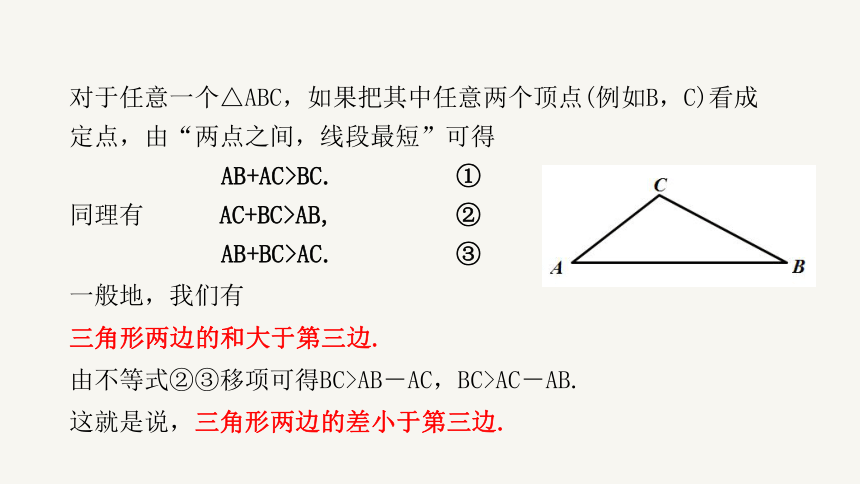
对于任意一个△ABC,如果把其中任意两个顶点(例如B,C)看成定点,由“两点之间,线段最短”可得
AB+AC>BC. ①
同理有 AC+BC>AB, ②
AB+BC>AC. ③
一般地,我们有
三角形两边的和大于第三边.
由不等式②③移项可得BC>AB-AC,BC>AC-AB.
这就是说,三角形两边的差小于第三边.
三角形两边的和大于第三边.
三角形两边的差小于第三边.
归纳总结:
对于三条线段,当它们满足什么条件时,这三
条线段能组成三角形?
(1)现有两根小棒,一根长3厘米,一根长5厘米,再配一根多长的小棒,就能围成一个三角形 猜想一下结果?
活动2
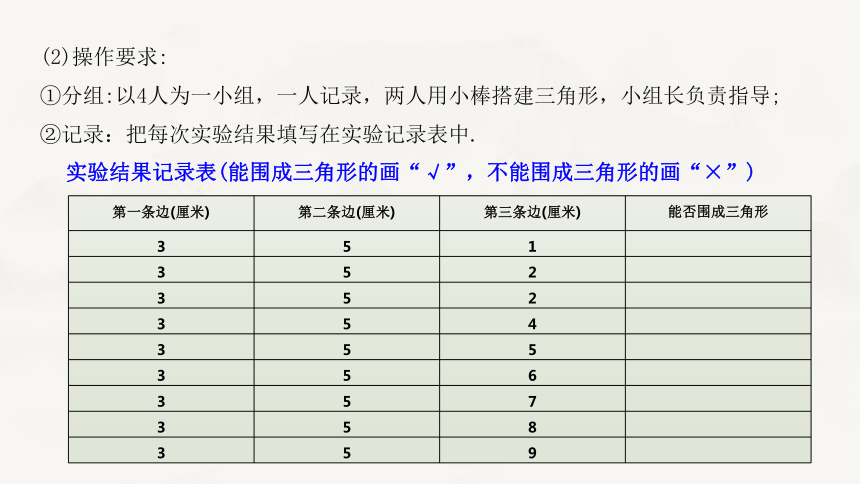
(2)操作要求:
①分组:以4人为一小组,一人记录,两人用小棒搭建三角形,小组长负责指导;
②记录:把每次实验结果填写在实验记录表中.
第一条边(厘米) 第二条边(厘米) 第三条边(厘米) 能否围成三角形
3 5 1
3 5 2
3 5 2
3 5 4
3 5 5
3 5 6
3 5 7
3 5 8
3 5 9
实验结果记录表(能围成三角形的画“√”,不能围成三角形的画“×”)
问题1 如果三条线段能围成三角形,那么这三条线段满足什么关系?
问题2 如果三条线段不能围成三角形,那么这三条线段满足什么关系?
一般地,如果三条线段中任意两条线段的和大于第三条线段,那么这三条线段能组成三角形;如果三条线段中有两条线段的和小于或等于第三条线段,那么这三条线段不能组成三角形.
归纳总结:
范例应用
例1 下列长度的三条线段能否组成三角形 为什么
(1) 3,4,5;(2)5,6,11;(3)10,6,3.
解:(1)能.因为3+4>5,3+5>4,4+5>3,
符合三角形两边的和大于第三边.
(2)不能.因为5+ 6 =11,
不符合三角形两边的和大于第三边.
(3)不能.因为6+3<10,
不符合三角形两边的和大于第三边.
只要满足较小的两条线段之和大于第三条线段,或较长线段与最短线段之差小于中间线段,便可构成三角形;若不满足,则不能构成三角形.
方法点拨
例2 用一条长为18 cm的细绳围成一个等腰三角形.
(1) 如果腰长是底边长的2倍,那么各边的长是多少?
(2) 能围成有一边的长是4 cm的等腰三角形吗?为什么?
解:(1)设底边长为x cm,则腰长为2x cm.
x+2x+2x = 18,解得x=3.6.
所以,三边长分别为3. 6 cm,7.2 cm,7.2 cm.
例题讲解
(2)因为长为4 cm的边可能是腰,也可能是底边,所以需要分情况讨论.
如果4 cm长的边为底边,设腰长为x cm,则 4+2x = 18.
解得x = 7.
如果4 cm长的边为腰,设底边长为 x cm,则
2×4+x = 18.
解得x = 10.
因为4+4<10,不符合三角形两边的和大于第三边,所以不能围成腰长 是4 cm的等腰三角形.
由以上讨论可知,可以围成底边长是4 cm的等腰三角形.
归纳:等腰三角形与三角形的三边关系结合时,若腰和底不明确,需要分类讨论,再检验是否符合三边关系.
即时测评
3.以长为3cm、5cm、7cm、10cm的四条线段中的 三条线段为边,可构成_____个三角形.
(1)任何三条线段都能组成一个三角形 . ( )
(2)因为a+b>c,所以a、b、c三边可以构成三角形. ( )
×
×
2
1.判断
2.已知等腰三角形的两边长分别为8cm,3cm,则这三角形的周长为 ( )
A. 14cm B.19cm C. 14cm或19cm D. 不确定
B
任务二 三角形的稳定性
工程建筑中经常采用三角形的结构,如屋顶钢架,其中的道理是什么?盖房子,在窗框未安装好之前,木工师傅常常在窗框上斜钉一根木条,为什么要这样做呢?
把同学们四人分成一组,发给3张硬纸条,3枚钉子,分组合作探究实验.如图所示,把三张硬纸条用钉子钉成一个三角形,然后扭动它,它的形状会改变吗 这说明什么问题
分析:
不会改变,也就是说,三角形的三条边长确定后,三角形的形状就确定了.
如果一个三角形的三条边固定了,那么三角形的形状和大小也就完全确定了,在数学上把三角形的这个性质叫作三角形的稳定性.
归纳总结:
活动1
同学们想一想,在现实生活中,三角形的稳定性有哪些方面的应用呢 举例子说明.
(3)房顶钢架做成三角形.
起重机的力臂
钢架
房顶钢架
三角形的稳定性:
(1)钢架桥的钢架做成三角形;
(2)起重机的力臂做成三角形;
活动2
当堂达标
叁
当堂达标
1. 用木棒钉成一个三角架,两根小棒长分别是
7 cm 和 10 cm,第三根小棒长可取 ( )
A. 2 cm B. 3 cm C. 11 cm D. 20 cm
C
2. 如图,工人师傅砌门时,常用木条EF固定门框ABCD,使其不变形,这种做法的根据是( )
A.两点之间线段最短
B.三角形两边之和大于第三边
C.长方形的四个角都是直角
D.三角形的稳定性
D
3. 已知等腰三角形的两边长分别为 5 cm,3 cm,则这个三角形的周长为 .
13 cm或11cm
注:等腰三角形中常要用到分类讨论思想,在涉及周长问题时要养成检验三边关系的好习惯哦!
4. 若三角形的两边长分别是 3 和 8,第三边长为奇数,求第三边的长.
解:设第三边长为 x,根据三角形的三边关系,可得
8 - 3<x<8 + 3,即 5<x<11
又因为 x 为奇数,所以 x = 7 或 9,
即第三边的长为 7 或 9.
5. 已知 a、b、c 为三角形的三边长,
化简:|b + c - a| + |b - c - a| - |c - a - b| - |a - b + c|.
∴ 原式 = |(b+c)-a| + |b-(c+a)| - |c-(a+b)| - |(a+c)-b|
= b + c - a + a + c - b - a - b + c + b - a – c
= 2c - 2a.
解:∵ a、b、c 为三角形三边的长,
∴ a + b>c,a + c>b,b + c>a.
解:有三条路可以走,走中间的路最近,理由是两点之间线段最短,或三角形的两边之和大于第三边.
6.如图所示,观察小明上学的示意图,有几条路可以走 你会选哪条路 请说说你选择的依据
课堂小结
肆
课堂小结
三角形
三边关系
原理
两点之间线段最短
内容
两边之和大于第三边
两边之差小于第三边
|a-b|b,x为第三边)
应用
分类讨论+检验
三角形的稳定性
课后作业
基础题:1.课后习题 第 1,2,5题。
提高题:2.请学有余力的同学完成课后习题第6题
谢
谢
第13章 三角形
13.2 与三角形有关的线段
13.2.1 三角形的边
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
(1)如图,老师这儿有三根小棒,谁能上来把它们围成一个三角形
(2)如图,换三根小棒,谁能上来把它们围成一个三角形
思考:
(2)你能得到什么结论?
(1)为什么有时三根木棒能围成三角形,有时三根木棒不能围成三角形?
新知初探
贰
新知初探
任务一 探究三角形的三边关系
如图是一个△ABC,假设有一只小狗从点A出发,沿三角形的边到点C吃香肠.小狗有几条路线可以选择
在A点的小狗,为了尽快吃到B点的香肠,它选择A B 路线,而不选择A C B路线,难道小狗也懂数学?
C
B
A
AC+CB>AB
两点之间,线段最短
活动1
对于任意一个△ABC,如果把其中任意两个顶点(例如B,C)看成定点,由“两点之间,线段最短”可得
AB+AC>BC. ①
同理有 AC+BC>AB, ②
AB+BC>AC. ③
一般地,我们有
三角形两边的和大于第三边.
由不等式②③移项可得BC>AB-AC,BC>AC-AB.
这就是说,三角形两边的差小于第三边.
三角形两边的和大于第三边.
三角形两边的差小于第三边.
归纳总结:
对于三条线段,当它们满足什么条件时,这三
条线段能组成三角形?
(1)现有两根小棒,一根长3厘米,一根长5厘米,再配一根多长的小棒,就能围成一个三角形 猜想一下结果?
活动2
(2)操作要求:
①分组:以4人为一小组,一人记录,两人用小棒搭建三角形,小组长负责指导;
②记录:把每次实验结果填写在实验记录表中.
第一条边(厘米) 第二条边(厘米) 第三条边(厘米) 能否围成三角形
3 5 1
3 5 2
3 5 2
3 5 4
3 5 5
3 5 6
3 5 7
3 5 8
3 5 9
实验结果记录表(能围成三角形的画“√”,不能围成三角形的画“×”)
问题1 如果三条线段能围成三角形,那么这三条线段满足什么关系?
问题2 如果三条线段不能围成三角形,那么这三条线段满足什么关系?
一般地,如果三条线段中任意两条线段的和大于第三条线段,那么这三条线段能组成三角形;如果三条线段中有两条线段的和小于或等于第三条线段,那么这三条线段不能组成三角形.
归纳总结:
范例应用
例1 下列长度的三条线段能否组成三角形 为什么
(1) 3,4,5;(2)5,6,11;(3)10,6,3.
解:(1)能.因为3+4>5,3+5>4,4+5>3,
符合三角形两边的和大于第三边.
(2)不能.因为5+ 6 =11,
不符合三角形两边的和大于第三边.
(3)不能.因为6+3<10,
不符合三角形两边的和大于第三边.
只要满足较小的两条线段之和大于第三条线段,或较长线段与最短线段之差小于中间线段,便可构成三角形;若不满足,则不能构成三角形.
方法点拨
例2 用一条长为18 cm的细绳围成一个等腰三角形.
(1) 如果腰长是底边长的2倍,那么各边的长是多少?
(2) 能围成有一边的长是4 cm的等腰三角形吗?为什么?
解:(1)设底边长为x cm,则腰长为2x cm.
x+2x+2x = 18,解得x=3.6.
所以,三边长分别为3. 6 cm,7.2 cm,7.2 cm.
例题讲解
(2)因为长为4 cm的边可能是腰,也可能是底边,所以需要分情况讨论.
如果4 cm长的边为底边,设腰长为x cm,则 4+2x = 18.
解得x = 7.
如果4 cm长的边为腰,设底边长为 x cm,则
2×4+x = 18.
解得x = 10.
因为4+4<10,不符合三角形两边的和大于第三边,所以不能围成腰长 是4 cm的等腰三角形.
由以上讨论可知,可以围成底边长是4 cm的等腰三角形.
归纳:等腰三角形与三角形的三边关系结合时,若腰和底不明确,需要分类讨论,再检验是否符合三边关系.
即时测评
3.以长为3cm、5cm、7cm、10cm的四条线段中的 三条线段为边,可构成_____个三角形.
(1)任何三条线段都能组成一个三角形 . ( )
(2)因为a+b>c,所以a、b、c三边可以构成三角形. ( )
×
×
2
1.判断
2.已知等腰三角形的两边长分别为8cm,3cm,则这三角形的周长为 ( )
A. 14cm B.19cm C. 14cm或19cm D. 不确定
B
任务二 三角形的稳定性
工程建筑中经常采用三角形的结构,如屋顶钢架,其中的道理是什么?盖房子,在窗框未安装好之前,木工师傅常常在窗框上斜钉一根木条,为什么要这样做呢?
把同学们四人分成一组,发给3张硬纸条,3枚钉子,分组合作探究实验.如图所示,把三张硬纸条用钉子钉成一个三角形,然后扭动它,它的形状会改变吗 这说明什么问题
分析:
不会改变,也就是说,三角形的三条边长确定后,三角形的形状就确定了.
如果一个三角形的三条边固定了,那么三角形的形状和大小也就完全确定了,在数学上把三角形的这个性质叫作三角形的稳定性.
归纳总结:
活动1
同学们想一想,在现实生活中,三角形的稳定性有哪些方面的应用呢 举例子说明.
(3)房顶钢架做成三角形.
起重机的力臂
钢架
房顶钢架
三角形的稳定性:
(1)钢架桥的钢架做成三角形;
(2)起重机的力臂做成三角形;
活动2
当堂达标
叁
当堂达标
1. 用木棒钉成一个三角架,两根小棒长分别是
7 cm 和 10 cm,第三根小棒长可取 ( )
A. 2 cm B. 3 cm C. 11 cm D. 20 cm
C
2. 如图,工人师傅砌门时,常用木条EF固定门框ABCD,使其不变形,这种做法的根据是( )
A.两点之间线段最短
B.三角形两边之和大于第三边
C.长方形的四个角都是直角
D.三角形的稳定性
D
3. 已知等腰三角形的两边长分别为 5 cm,3 cm,则这个三角形的周长为 .
13 cm或11cm
注:等腰三角形中常要用到分类讨论思想,在涉及周长问题时要养成检验三边关系的好习惯哦!
4. 若三角形的两边长分别是 3 和 8,第三边长为奇数,求第三边的长.
解:设第三边长为 x,根据三角形的三边关系,可得
8 - 3<x<8 + 3,即 5<x<11
又因为 x 为奇数,所以 x = 7 或 9,
即第三边的长为 7 或 9.
5. 已知 a、b、c 为三角形的三边长,
化简:|b + c - a| + |b - c - a| - |c - a - b| - |a - b + c|.
∴ 原式 = |(b+c)-a| + |b-(c+a)| - |c-(a+b)| - |(a+c)-b|
= b + c - a + a + c - b - a - b + c + b - a – c
= 2c - 2a.
解:∵ a、b、c 为三角形三边的长,
∴ a + b>c,a + c>b,b + c>a.
解:有三条路可以走,走中间的路最近,理由是两点之间线段最短,或三角形的两边之和大于第三边.
6.如图所示,观察小明上学的示意图,有几条路可以走 你会选哪条路 请说说你选择的依据
课堂小结
肆
课堂小结
三角形
三边关系
原理
两点之间线段最短
内容
两边之和大于第三边
两边之差小于第三边
|a-b|
应用
分类讨论+检验
三角形的稳定性
课后作业
基础题:1.课后习题 第 1,2,5题。
提高题:2.请学有余力的同学完成课后习题第6题
谢
谢
同课章节目录
