第二十四章 圆综合检测题(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十四章 圆综合检测题
一、单选题
1.(2024九下·兰陵模拟)如图,△ABC内接于⊙O,若∠A=45°,OC=2,则BC的长为( )
A. B. C. D.4
2.下面四个判断中正确的是( ).
A.过圆内一点(非圆心)的无数条弦中,有最长的弦,没有最短的弦
B.过圆内一点(非圆心)的无数条弦中,有最短的弦,没有最长的弦
C.过圆内一点(非圆心)的无数条弦中,有且只有一条最长的弦,也有且只有一条最短的弦
D.过圆内一点(非圆心)的无数条弦中,既没有最长的弦,也没有最短的弦
3.(2021九上·南京月考)已知AB是⊙O的直径,过点A的弦AD平行于半径OC,若∠A=70°,则∠B等于( )
A.30° B.35° C.40° D.60°
4.(2021九上·长沙期中)下列四个命题:①直角三角形斜边上的中线等于斜边的一半;②对角线相等的平行四边形是菱形;⑨一组邻边相等的矩形是正方形;④三角形三条角平分线的交点是三角形的外心.其中真命题共有( )
A.1个 B.2个 C.3个 D.4个
5.(2024九上·吉林期中)如图,在中,弦于点C,,,则的长为( )
A.17 B.15 C. D.3
6.(2024九上·滨湖期末)若等腰△ABC内接于⊙O,AB=AC,∠BOC=100°,则△ABC底角的度数为( )
A.65° B.25° C.65°或25° D.65°或30°
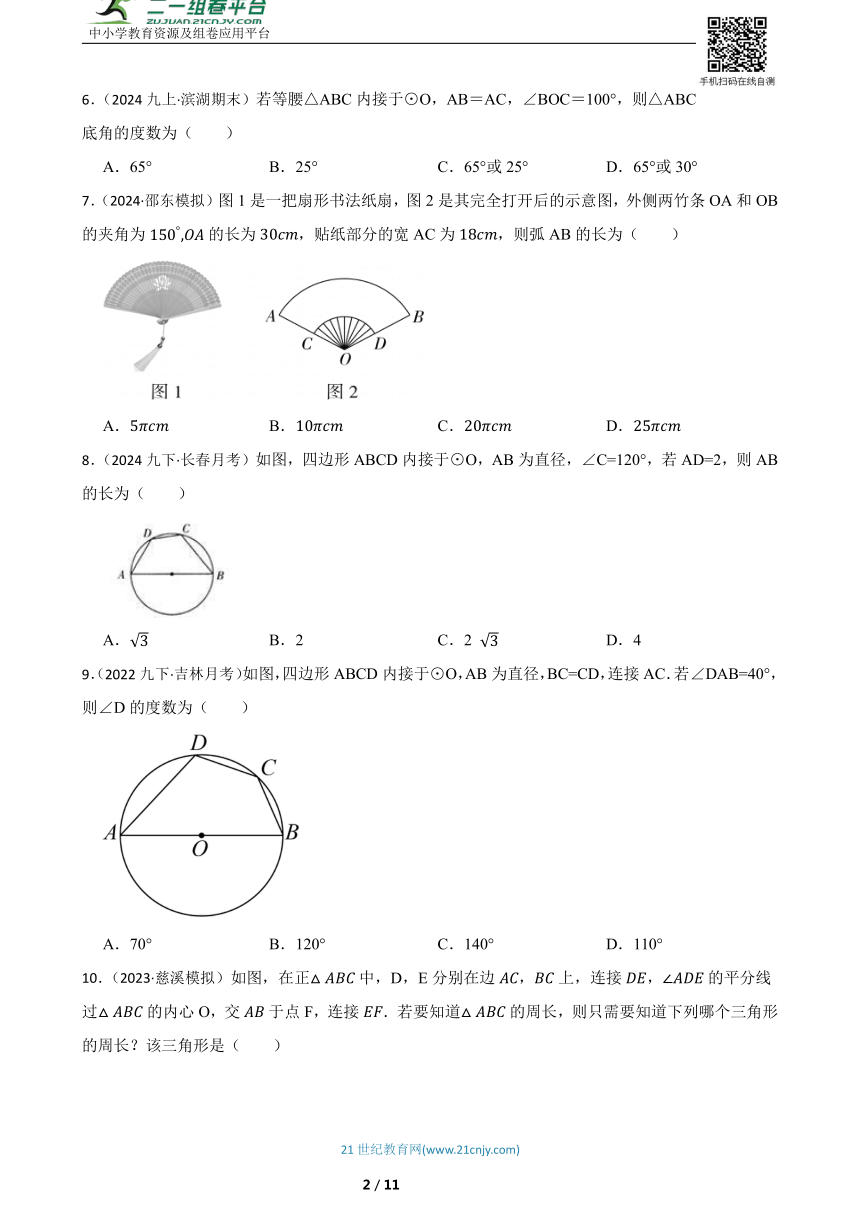
7.(2024·邵东模拟)图1是一把扇形书法纸扇,图2是其完全打开后的示意图,外侧两竹条OA和OB的夹角为的长为,贴纸部分的宽AC为,则弧AB的长为( )
A. B. C. D.
8.(2024九下·长春月考)如图,四边形ABCD内接于⊙O,AB为直径,∠C=120°,若AD=2,则AB的长为( )
A. B.2 C.2 D.4
9.(2022九下·吉林月考)如图,四边形ABCD内接于⊙O,AB为直径,BC=CD,连接AC.若∠DAB=40°,则∠D的度数为( )
A.70° B.120° C.140° D.110°
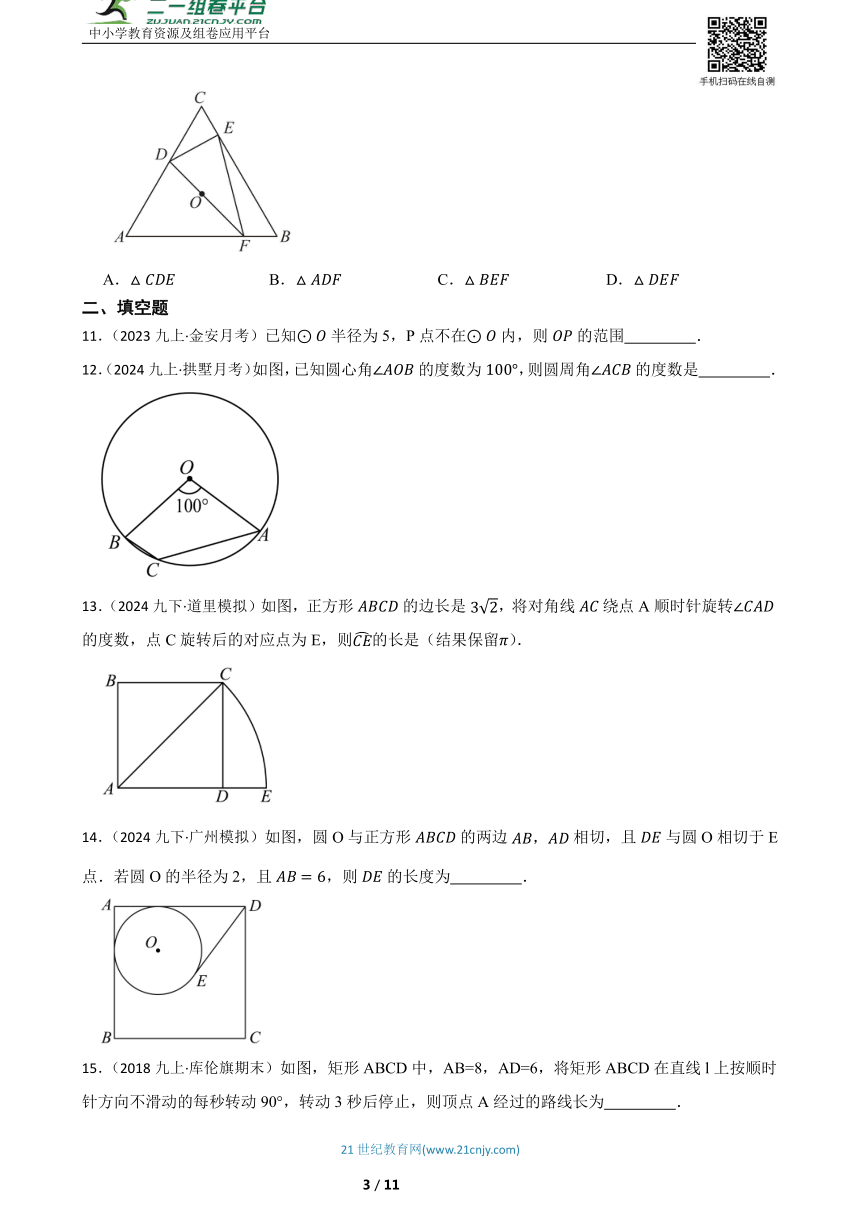
10.(2023·慈溪模拟)如图,在正中,D,E分别在边,上,连接,的平分线过的内心O,交于点F,连接.若要知道的周长,则只需要知道下列哪个三角形的周长?该三角形是( )
A. B. C. D.
二、填空题
11.(2023九上·金安月考)已知半径为5,P点不在内,则的范围 .
12.(2024九上·拱墅月考)如图,已知圆心角的度数为,则圆周角的度数是 .
13.(2024九下·道里模拟)如图,正方形的边长是,将对角线绕点A顺时针旋转的度数,点C旋转后的对应点为E,则的长是(结果保留).
14.(2024九下·广州模拟)如图,圆O与正方形的两边相切,且与圆O相切于E点.若圆O的半径为2,且,则的长度为 .
15.(2018九上·库伦旗期末)如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD在直线l上按顺时针方向不滑动的每秒转动90°,转动3秒后停止,则顶点A经过的路线长为 .
16.(2022九下·重庆开学考)已知:如图,在Rt△ABC中,∠ABC=90°,AC=12,BC=6,以AB为直径的圆与以BC为直径的圆交AC于点D,则图中阴影部分的面积为 .
三、计算题
17.(2024九上·分宜月考)如图,正三角形、正方形、正六边形等正n边形与圆的形状有差异,我们将正n边形与圆的接近程度称为“接近度”.
(1)角的“接近度”定义:设正n边形的每个内角的度数为,将正n边形的“接近度”定义为.于是越小,该正n边形就越接近于圆,
①若,则该正n边形的“接近度”等于 .
②若,则该正n边形的“接近度”等于______.
③当“接近度”等于______.时,正n边形就成了圆.
(2)边的“接近度”定义:设一个正n边形的外接圆的半径为R,正n边形的中心到各边的距离为d,将正n边形的“接近度”定义为.分别计算时边的“接近度”,并猜测当边的“接近度”等于多少时,正n边形就成了圆?
18.(2023九上·吴兴期中)根据以下素材,探索完成任务.
【问题】如何设计隧道内车道的限高及车道宽方案?
【素材一】图1隧道是一段圆弧拱形结构,图2是它的示意图.经测量,拱形跨度16m,拱顶离地面4m.
【素材二】如图3,某道路规划部门计划将左侧公路分为非机动车道、机动车道一、机动车道二及绿化带四部分,原计划设计非机动车道宽2m,每条机动车道宽均2.5m.为了保证车辆的行驶安全,高架下方需要设置限高标志以警示车辆驾驶员.(限高即图中的高度)
【素材三】如图4,由于城市道路绿化需求,道路规划部门确定新方案为在非机动车道和机动车道一之间增加一条0.5m的绿化带,非机动车道最高高度不低于1.8m,中间绿化带宽度不变,每条机动车道道宽相等.
【任务一】确定隧道所在圆弧的半径.
【任务二】探究原计划该隧道下方机动车道一的限高要求.
【任务三】新方案下当机动车宽度最大的情况下,机动车道的宽度与原来相比是变宽了还是变窄了?求出新方案下机动车道的最大宽度.
19.(2023九上·青秀期中)【综合与实践】
【问题情境】在学习了数学活动《车轮做成圆形的数学道理》后,数学学习小组的同学们利用计算机软件继续模拟并探讨各种不同类型的图形的滚动问题.
【实践探究】同学们首先选择了以下四种正多边形沿水平地面的滚动,研究了以一个顶点为支点完成一次完整旋转的过程.例如,在图一中,等边三角形围绕顶点,中心从顺时针旋转到再到的过程.我们定义这个旋转过程为正多边形绕一个顶点的一次旋转.
(1)我们学习了图二中正方形绕一个顶点的一次旋转角度为,即是正方形的中心角度数,也是外角度数.那么等边三角形绕一个顶点的一次旋转角度为______;正五边形绕一个顶点的一次旋转角度为______;正边形绕一个顶点的一次旋转角度为______;
【深入探究】同学们继续模拟并探究,如果不是沿着水平地面滚动又会是怎样的情况?
(2)如图五,半径为2的正五边形在另一个相同半径的正五边形的边上顺时针滚动,初始时正五边形绕顶点的一次旋转中,中心旋转到,则这一次旋转的旋转角度是多大?沿正五边形滚动一周后回到原来的位置,中心的运动路径长为多少?
【问题解决】如果将正多边形变化为其他图形又会是怎样的情况呢?
(3)如图六,点为上的点,,,由弦及弧组成的类似扇形的图形沿着水平地面顺时针滚动一周,直接写出圆心的运动路径的长.
四、解答题
20.如图所示,在一个长度为8的梯子AB的顶点向点滑动的过程中,梯子的两端A,B与墙的底端构成的三角形的外心与点的距离是否发生变化 若发生变化,请说明理由;若不发生变化,请求出其长度.
21.(2024九上·苏州月考)如图,是⊙O的弦,C是⊙O上的一点,且,于点E,交⊙O于点D.若⊙O的半径为6,求弦的长.
22.(2019九上·江夏期末)每个小方格是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系的位置如图所示.将菱形OABC绕原点O顺时针旋转90°菱形OA1B1C1,请画出菱形OA1B1C1,并求出点B旋转到点B1的路径长.
23.(2024·坪山模拟)如图,在中,点O,D分别为AB,BC的中点,连接OD,作与AC相切于点,在AC边上取一点,使,连接DF.
(1)判断直线DF与的位置关系,并说明理由;
(2)当时,求的半径.
答案解析部分
1.【答案】B
【知识点】勾股定理;圆周角定理
2.【答案】C
【知识点】圆的相关概念;垂径定理
3.【答案】B
【知识点】平行线的性质;圆周角定理
4.【答案】B
【知识点】矩形的判定;正方形的判定;三角形的内切圆与内心;直角三角形斜边上的中线;真命题与假命题
5.【答案】C
【知识点】勾股定理;垂径定理
6.【答案】C
【知识点】圆周角定理;圆内接四边形的性质
7.【答案】D
【知识点】弧长的计算
8.【答案】D
【知识点】圆内接四边形的性质
9.【答案】D
【知识点】圆周角定理;圆内接四边形的性质
10.【答案】A
【知识点】直角三角形全等的判定-HL;角平分线的性质;等边三角形的判定与性质;三角形的内切圆与内心
11.【答案】
【知识点】点与圆的位置关系
12.【答案】
【知识点】圆周角定理;圆内接四边形的性质
13.【答案】
【知识点】勾股定理;正方形的性质;弧长的计算
14.【答案】4
【知识点】正方形的判定与性质;切线的性质;切线长定理
15.【答案】
【知识点】弧长的计算;旋转的性质
16.【答案】 -3
【知识点】三角形的面积;等边三角形的判定与性质;勾股定理;扇形面积的计算;直角三角形斜边上的中线
17.【答案】(1)①120;②18;③0
(2)时,;时,,当边的“接近度”等于0时,正n边形就成了圆
【知识点】多边形内角与外角;圆内接正多边形
18.【答案】【一】10m
【二】2m
【三】变窄了,
【知识点】勾股定理;垂径定理
19.【答案】(1);(2);;(3)
【知识点】多边形内角与外角;圆内接正多边形;弧长的计算
20.【答案】解:不发生变化,理由如下:
∵梯子的两端A,B与墙的底端C构成的三角形为直角三角形,
∴外心和与点C的距离始终为AB,
∴不发生变化,其长度为×8=4.
【知识点】三角形的外接圆与外心;直角三角形斜边上的中线
21.【答案】
【知识点】含30°角的直角三角形;勾股定理;垂径定理;圆周角定理
22.【答案】解:如图,菱形OA1B1C1即为所求;
∵OB= =4 ,
∴点B旋转到点B1的路径长= =2 π.
【知识点】弧长的计算;旋转的性质;坐标与图形变化﹣旋转
23.【答案】(1)解:直线与相切,理由如下:
如图,连接OE,过点O作于点P
相切于点
,OE为的半径
点,分别为,的中点
四边形ODCE是矩形
在和中,
,即OP为的半径
则直线与相切;
(2)解:设的半径为,则,
点,分别为,的中点
在中,
由(1)已证:
在中,,即
解得或(不符题意,舍去)
故的半径为1.
【知识点】勾股定理;矩形的判定与性质;切线的判定与性质;三角形全等的判定-SAS;三角形的中位线定理
21世纪教育网(www.21cnjy.com)
1 / 11
第二十四章 圆综合检测题
一、单选题
1.(2024九下·兰陵模拟)如图,△ABC内接于⊙O,若∠A=45°,OC=2,则BC的长为( )
A. B. C. D.4
2.下面四个判断中正确的是( ).
A.过圆内一点(非圆心)的无数条弦中,有最长的弦,没有最短的弦
B.过圆内一点(非圆心)的无数条弦中,有最短的弦,没有最长的弦
C.过圆内一点(非圆心)的无数条弦中,有且只有一条最长的弦,也有且只有一条最短的弦
D.过圆内一点(非圆心)的无数条弦中,既没有最长的弦,也没有最短的弦
3.(2021九上·南京月考)已知AB是⊙O的直径,过点A的弦AD平行于半径OC,若∠A=70°,则∠B等于( )
A.30° B.35° C.40° D.60°
4.(2021九上·长沙期中)下列四个命题:①直角三角形斜边上的中线等于斜边的一半;②对角线相等的平行四边形是菱形;⑨一组邻边相等的矩形是正方形;④三角形三条角平分线的交点是三角形的外心.其中真命题共有( )
A.1个 B.2个 C.3个 D.4个
5.(2024九上·吉林期中)如图,在中,弦于点C,,,则的长为( )
A.17 B.15 C. D.3
6.(2024九上·滨湖期末)若等腰△ABC内接于⊙O,AB=AC,∠BOC=100°,则△ABC底角的度数为( )
A.65° B.25° C.65°或25° D.65°或30°
7.(2024·邵东模拟)图1是一把扇形书法纸扇,图2是其完全打开后的示意图,外侧两竹条OA和OB的夹角为的长为,贴纸部分的宽AC为,则弧AB的长为( )
A. B. C. D.
8.(2024九下·长春月考)如图,四边形ABCD内接于⊙O,AB为直径,∠C=120°,若AD=2,则AB的长为( )
A. B.2 C.2 D.4
9.(2022九下·吉林月考)如图,四边形ABCD内接于⊙O,AB为直径,BC=CD,连接AC.若∠DAB=40°,则∠D的度数为( )
A.70° B.120° C.140° D.110°
10.(2023·慈溪模拟)如图,在正中,D,E分别在边,上,连接,的平分线过的内心O,交于点F,连接.若要知道的周长,则只需要知道下列哪个三角形的周长?该三角形是( )
A. B. C. D.
二、填空题
11.(2023九上·金安月考)已知半径为5,P点不在内,则的范围 .
12.(2024九上·拱墅月考)如图,已知圆心角的度数为,则圆周角的度数是 .
13.(2024九下·道里模拟)如图,正方形的边长是,将对角线绕点A顺时针旋转的度数,点C旋转后的对应点为E,则的长是(结果保留).
14.(2024九下·广州模拟)如图,圆O与正方形的两边相切,且与圆O相切于E点.若圆O的半径为2,且,则的长度为 .
15.(2018九上·库伦旗期末)如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD在直线l上按顺时针方向不滑动的每秒转动90°,转动3秒后停止,则顶点A经过的路线长为 .
16.(2022九下·重庆开学考)已知:如图,在Rt△ABC中,∠ABC=90°,AC=12,BC=6,以AB为直径的圆与以BC为直径的圆交AC于点D,则图中阴影部分的面积为 .
三、计算题
17.(2024九上·分宜月考)如图,正三角形、正方形、正六边形等正n边形与圆的形状有差异,我们将正n边形与圆的接近程度称为“接近度”.
(1)角的“接近度”定义:设正n边形的每个内角的度数为,将正n边形的“接近度”定义为.于是越小,该正n边形就越接近于圆,
①若,则该正n边形的“接近度”等于 .
②若,则该正n边形的“接近度”等于______.
③当“接近度”等于______.时,正n边形就成了圆.
(2)边的“接近度”定义:设一个正n边形的外接圆的半径为R,正n边形的中心到各边的距离为d,将正n边形的“接近度”定义为.分别计算时边的“接近度”,并猜测当边的“接近度”等于多少时,正n边形就成了圆?
18.(2023九上·吴兴期中)根据以下素材,探索完成任务.
【问题】如何设计隧道内车道的限高及车道宽方案?
【素材一】图1隧道是一段圆弧拱形结构,图2是它的示意图.经测量,拱形跨度16m,拱顶离地面4m.
【素材二】如图3,某道路规划部门计划将左侧公路分为非机动车道、机动车道一、机动车道二及绿化带四部分,原计划设计非机动车道宽2m,每条机动车道宽均2.5m.为了保证车辆的行驶安全,高架下方需要设置限高标志以警示车辆驾驶员.(限高即图中的高度)
【素材三】如图4,由于城市道路绿化需求,道路规划部门确定新方案为在非机动车道和机动车道一之间增加一条0.5m的绿化带,非机动车道最高高度不低于1.8m,中间绿化带宽度不变,每条机动车道道宽相等.
【任务一】确定隧道所在圆弧的半径.
【任务二】探究原计划该隧道下方机动车道一的限高要求.
【任务三】新方案下当机动车宽度最大的情况下,机动车道的宽度与原来相比是变宽了还是变窄了?求出新方案下机动车道的最大宽度.
19.(2023九上·青秀期中)【综合与实践】
【问题情境】在学习了数学活动《车轮做成圆形的数学道理》后,数学学习小组的同学们利用计算机软件继续模拟并探讨各种不同类型的图形的滚动问题.
【实践探究】同学们首先选择了以下四种正多边形沿水平地面的滚动,研究了以一个顶点为支点完成一次完整旋转的过程.例如,在图一中,等边三角形围绕顶点,中心从顺时针旋转到再到的过程.我们定义这个旋转过程为正多边形绕一个顶点的一次旋转.
(1)我们学习了图二中正方形绕一个顶点的一次旋转角度为,即是正方形的中心角度数,也是外角度数.那么等边三角形绕一个顶点的一次旋转角度为______;正五边形绕一个顶点的一次旋转角度为______;正边形绕一个顶点的一次旋转角度为______;
【深入探究】同学们继续模拟并探究,如果不是沿着水平地面滚动又会是怎样的情况?
(2)如图五,半径为2的正五边形在另一个相同半径的正五边形的边上顺时针滚动,初始时正五边形绕顶点的一次旋转中,中心旋转到,则这一次旋转的旋转角度是多大?沿正五边形滚动一周后回到原来的位置,中心的运动路径长为多少?
【问题解决】如果将正多边形变化为其他图形又会是怎样的情况呢?
(3)如图六,点为上的点,,,由弦及弧组成的类似扇形的图形沿着水平地面顺时针滚动一周,直接写出圆心的运动路径的长.
四、解答题
20.如图所示,在一个长度为8的梯子AB的顶点向点滑动的过程中,梯子的两端A,B与墙的底端构成的三角形的外心与点的距离是否发生变化 若发生变化,请说明理由;若不发生变化,请求出其长度.
21.(2024九上·苏州月考)如图,是⊙O的弦,C是⊙O上的一点,且,于点E,交⊙O于点D.若⊙O的半径为6,求弦的长.
22.(2019九上·江夏期末)每个小方格是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系的位置如图所示.将菱形OABC绕原点O顺时针旋转90°菱形OA1B1C1,请画出菱形OA1B1C1,并求出点B旋转到点B1的路径长.
23.(2024·坪山模拟)如图,在中,点O,D分别为AB,BC的中点,连接OD,作与AC相切于点,在AC边上取一点,使,连接DF.
(1)判断直线DF与的位置关系,并说明理由;
(2)当时,求的半径.
答案解析部分
1.【答案】B
【知识点】勾股定理;圆周角定理
2.【答案】C
【知识点】圆的相关概念;垂径定理
3.【答案】B
【知识点】平行线的性质;圆周角定理
4.【答案】B
【知识点】矩形的判定;正方形的判定;三角形的内切圆与内心;直角三角形斜边上的中线;真命题与假命题
5.【答案】C
【知识点】勾股定理;垂径定理
6.【答案】C
【知识点】圆周角定理;圆内接四边形的性质
7.【答案】D
【知识点】弧长的计算
8.【答案】D
【知识点】圆内接四边形的性质
9.【答案】D
【知识点】圆周角定理;圆内接四边形的性质
10.【答案】A
【知识点】直角三角形全等的判定-HL;角平分线的性质;等边三角形的判定与性质;三角形的内切圆与内心
11.【答案】
【知识点】点与圆的位置关系
12.【答案】
【知识点】圆周角定理;圆内接四边形的性质
13.【答案】
【知识点】勾股定理;正方形的性质;弧长的计算
14.【答案】4
【知识点】正方形的判定与性质;切线的性质;切线长定理
15.【答案】
【知识点】弧长的计算;旋转的性质
16.【答案】 -3
【知识点】三角形的面积;等边三角形的判定与性质;勾股定理;扇形面积的计算;直角三角形斜边上的中线
17.【答案】(1)①120;②18;③0
(2)时,;时,,当边的“接近度”等于0时,正n边形就成了圆
【知识点】多边形内角与外角;圆内接正多边形
18.【答案】【一】10m
【二】2m
【三】变窄了,
【知识点】勾股定理;垂径定理
19.【答案】(1);(2);;(3)
【知识点】多边形内角与外角;圆内接正多边形;弧长的计算
20.【答案】解:不发生变化,理由如下:
∵梯子的两端A,B与墙的底端C构成的三角形为直角三角形,
∴外心和与点C的距离始终为AB,
∴不发生变化,其长度为×8=4.
【知识点】三角形的外接圆与外心;直角三角形斜边上的中线
21.【答案】
【知识点】含30°角的直角三角形;勾股定理;垂径定理;圆周角定理
22.【答案】解:如图,菱形OA1B1C1即为所求;
∵OB= =4 ,
∴点B旋转到点B1的路径长= =2 π.
【知识点】弧长的计算;旋转的性质;坐标与图形变化﹣旋转
23.【答案】(1)解:直线与相切,理由如下:
如图,连接OE,过点O作于点P
相切于点
,OE为的半径
点,分别为,的中点
四边形ODCE是矩形
在和中,
,即OP为的半径
则直线与相切;
(2)解:设的半径为,则,
点,分别为,的中点
在中,
由(1)已证:
在中,,即
解得或(不符题意,舍去)
故的半径为1.
【知识点】勾股定理;矩形的判定与性质;切线的判定与性质;三角形全等的判定-SAS;三角形的中位线定理
21世纪教育网(www.21cnjy.com)
1 / 11
同课章节目录
