25.3 用频率估计概率 同步练习(含答案)
文档属性
| 名称 | 25.3 用频率估计概率 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 234.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-09 11:02:54 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
25.3 用频率估计概率
一、单选题
1.(2019九上·城固期中)已知不透明的袋中只装有黑、白两种球,这些球除颜色外都相同,其中白球有2个,黑球有n个.随机地从袋子中摸出一个球,记录下颜色后,放回袋子中并摇匀.经过大量重复试验发现摸出白球的频率稳定在0.4附近,则n的值为( )
A.2 B.3 C.4 D.5
2.(2024七上·深圳期末)在“世界无烟日”来临之际,小明和他的同学为了解某街道大约有多少成年人吸烟,于是随机调查了该街道个成年人,结果有个成年人吸烟.对于这个数据的收集与处理过程,下列说法正确的是( )
A.调查的方式是普查 B.该街道约有的成年人吸烟
C.该街道只有个成年人不吸烟 D.样本是个吸烟的成年人
3.(2024七下·利津期末)下列说法合理的是( )
A.某彩票的中奖机会是,那么如果买100张彩票一定会有3张中奖
B.在一次课堂进行的实验中,甲、乙两组同学估计硬币落地后,正面朝上的频率分别为和
C.抛掷一枚正六面体骰子,出现2的概率是的意思是,每6次就有1次掷得2
D.任意画一个三角形,其内角和是是随机事件
4.(2024九上·大东月考)在一个不透明的纸箱中,内有蓝色、红色的玻璃球共16个,这些玻璃球除颜色外都相同.小何每次摸出一个球后放回,通过多次摸球试验后发现摸到蓝色玻璃球的频率稳定在,则纸箱中红色玻璃球很可能有( )
A.4个 B.8个 C.12个 D.16个
5.(2021九上·皇姑月考)一个口袋中有红球、白球共10个,这些球除颜色外都相同,将口袋中的球搅拌均匀,从中随机模出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有78次摸到红球,则口袋中白球的个数大约有( )
A.7个 B.8个 C.2个 D.3个
6.在一个不透明的口袋中放着红色、黑色、黄色的橡皮球共有30个,它们除颜色外其它全相同.小刚通过多次摸球试验后发现从中摸到红色球或黄色球的频率稳定在0.15和0.45之间,则口袋中黑色球的个数可能是 ( )
A.14 B.20 C.9 D.6
7.(2019九上·望城期中)下表记录了一名球员在罚球线上罚篮的结果:
投篮次数n 100 150 300 500 800 1000
投中次数m 58 96 17.4 302 484 601
投中频率n/m 0.580 0.640 0.580 0.604 0.605 0.601
这名球员投篮一次,投中的概率约是( )
A.0.58 B.0.6 C.0.64 D.0.55
8.(2020九上·河口期末)小张承包了一片荒山,他想把这片荒山改造成一个橡胶园,现在有一种橡胶树树苗,它的成活率如下表所示,则下面推断中,其中合理的是( ).
移植棵数 成活数 成活率 移植棵数 成活数 成活率
50 47 1500 1335
270 235 3500 3203
400 369 0.923 7000 6335
750 662 14000 12628
下面有四个推断:
①小张移植3500棵这种树苗,成活率肯定高于 ;②随着移植棵数的增加,树苗成活的频率总在 附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是 ;③若小张移植10000棵这种树苗,则可能成活9000棵;④若小张移植20000棵这种树苗,则一定成活率18000棵.
A.①② B.①④ C.②③ D.②④
9.在一个暗箱里放有x个除颜色外其它完全相同的球,这x个球中白球只有5个.每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到白球的频率稳定在20%,那么可以推算出x大约是( )
A.20 B.25 C.30 D.40
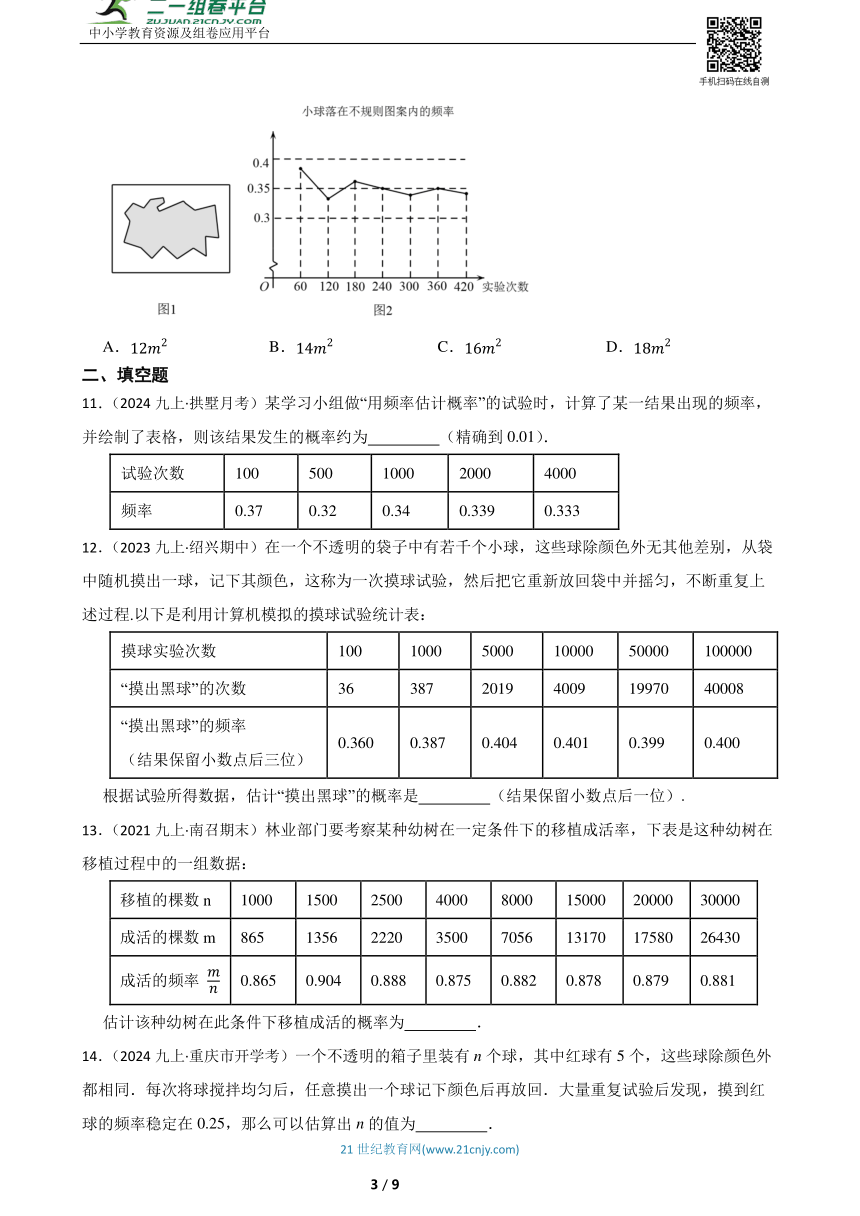
10.(2025八下·沛县月考)如图1所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为,宽为的长方形,将不规则图案围起来,然后在适当位置随机朝长方形区域扔小球,并记录小球落在不规则图案上的次数(小球扔在界线上或长方形区域外不计入试验结果),他将若干次有效试验的结果绘制成了图2所示的折线统计图,由此可估计不规则图案的面积大约是( )
A. B. C. D.
二、填空题
11.(2024九上·拱墅月考)某学习小组做“用频率估计概率”的试验时,计算了某一结果出现的频率,并绘制了表格,则该结果发生的概率约为 (精确到0.01).
试验次数 100 500 1000 2000 4000
频率 0.37 0.32 0.34 0.339 0.333
12.(2023九上·绍兴期中)在一个不透明的袋子中有若千个小球,这些球除颜色外无其他差别,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,然后把它重新放回袋中并摇匀,不断重复上述过程.以下是利用计算机模拟的摸球试验统计表:
摸球实验次数 100 1000 5000 10000 50000 100000
“摸出黑球”的次数 36 387 2019 4009 19970 40008
“摸出黑球”的频率 (结果保留小数点后三位) 0.360 0.387 0.404 0.401 0.399 0.400
根据试验所得数据,估计“摸出黑球”的概率是 (结果保留小数点后一位).
13.(2021九上·南召期末)林业部门要考察某种幼树在一定条件下的移植成活率,下表是这种幼树在移植过程中的一组数据:
移植的棵数n 1000 1500 2500 4000 8000 15000 20000 30000
成活的棵数m 865 1356 2220 3500 7056 13170 17580 26430
成活的频率 0.865 0.904 0.888 0.875 0.882 0.878 0.879 0.881
估计该种幼树在此条件下移植成活的概率为 .
14.(2024九上·重庆市开学考)一个不透明的箱子里装有n个球,其中红球有5个,这些球除颜色外都相同.每次将球搅拌均匀后,任意摸出一个球记下颜色后再放回.大量重复试验后发现,摸到红球的频率稳定在0.25,那么可以估算出n的值为 .
15.(2023九上·新罗月考)某林业部门要考察某种幼树在一定条件下的移植成活率,在同样条件下,对这种幼树进行大量移植,并完成统计情况,得到一组统计数据:
移植总次数n 1500 3500 7000 9000 14000
成活数m 1335 3203 6335 8037 12628
成活的频率
估计该种幼树在此条件下移植成活的概率是 (结果精确到0.1).
16.(2025九上·清新期末)一口袋中有6个红球和若干个白球,除颜色外均相同,从口袋中随机摸出一球,记下颜色,再把它放回口袋中摇匀.重复上述实验共300次,其中120次摸到红球,则口袋中大约有 个白球.
三、计算题
17.(2024九上·余杭月考)某校生物兴趣小组在相同的试验条件下,对某植物种子发芽率进行试验研究时,收集的试验结果如表所示:
试验的种子粒数(n) 500 1000 1500 2000 3000 4000
发芽的种子粒数(m) 471 946 1425 1898 2853 3812
发芽频率 x
(1)求表中x的值;
(2)任取一粒这种植物的种子,请你估计它能发芽的概率(精确到);
(3)若该学校劳动基地需要这种植物幼苗7600株,试估算该小组至少需要准备多少粒种子进行发芽培育.
18.(2024七下·贵阳月考)研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,记录球的颜色,放回盒中,然后重复上述过程.
活动结果:摸球实验活动一共做了50次,统计结果如下表:
球的颜色 无记号 有记号
红色 黄色 红色 黄色
摸到的次数 18 28 2 2
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
四、解答题
19.(2024九上·白银期末)在一个不透明的箱子中装有形状、大小均一样的小球,其中红色小球有3个,白色小球有1个.
(1)小远从箱子中任意摸出1个小球,则刚好摸出白色小球的概率为________.
(2)小远将前面摸出的1个小球放回箱子,又放入个白色小球,摇晃均匀后任意摸出1个小球,记下颜色,经过大量反复的试验,发现摸到白色小球的概率约为,求的值.
20.(2024八下·泗阳期中)在一个不透明的布袋中装有黄、白两种颜色的球共40只,这些球除颜色外其余均相同.小红按如下规则做摸球实验:将这些球搅匀后从中随机摸出一只球,记下颜色后再把球放回布袋中,不断重复上述过程. 下表是实验得到的一组统计数据:
摸球的次数 50 100 200 300 500 1 000 2000 3 000
摸到黄球的频数 36 67 128 176 306 593 1256 1803
摸到黄球的频率 0.72 0.67 0.64 0.59 0.61 0.59 0.63 0.60
(1)对实验得到的数据,选用“扇形统计图”、“条形统计图”或“折线统计图”中的 (填
写一种),能使我们更好地观察摸到黄球频率的变化情况;
(2)请估计:①当摸球次数很大时,摸到黄球的频率将会接近 ;(精确到0.1)
②若从布袋中随机摸出一只球,则摸到白球的概率为 ;(精确到0.1)
(3)试估算布袋中黄球的只数.
21.在一个不透明的盒子里装有黑、白两种颜色的球共40个,小颖做摸球试验.她将盒子里面的球搅匀后从中随机摸出一个球,记下颜色,然后把它放回盒子中.不断重复上述过程.如图所示为“摸到白球”的频率折线统计图.
(1)请估计:当n足够大时,摸到白球的频率将会接近 (结果精确到0.1),假如你摸一次,你摸到白球的概率为
(2)试估算盒子里白、黑两种颜色的球各有多少个.
(3)在(2)的条件下,如果要使摸到白球的频率稳定在,需要往盒子里再放入多少个白球?
22.(2017·滨州)为了考察甲、乙两种成熟期小麦的株高长势情况,现从中随机抽取6株,并测得它们的株高(单位:cm)如下表所示:
甲 63 66 63 61 64 61
乙 63 65 60 63 64 63
(Ⅰ)请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐?
(Ⅱ)现将进行两种小麦优良品种杂交实验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对情况,请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
答案解析部分
1.【答案】B
【知识点】利用频率估计概率
2.【答案】B
【知识点】全面调查与抽样调查;总体、个体、样本、样本容量;用样本估计总体;利用频率估计概率
3.【答案】B
【知识点】可能性的大小;概率的意义;利用频率估计概率;概率公式
4.【答案】C
【知识点】利用频率估计概率
5.【答案】C
【知识点】利用频率估计概率
6.【答案】B
【知识点】利用频率估计概率
7.【答案】B
【知识点】利用频率估计概率
8.【答案】C
【知识点】利用频率估计概率
9.【答案】B
【知识点】利用频率估计概率
10.【答案】B
【知识点】几何概率;利用频率估计概率
11.【答案】0.33
【知识点】利用频率估计概率
12.【答案】0.4
【知识点】利用频率估计概率
13.【答案】0.880
【知识点】利用频率估计概率
14.【答案】20
【知识点】利用频率估计概率
15.【答案】0.9
【知识点】利用频率估计概率
16.【答案】9
【知识点】利用频率估计概率
17.【答案】(1)
(2)
(3)
【知识点】利用频率估计概率
18.【答案】(1)红球占40%,黄球占60%;(2)盒中红球有40个.
【知识点】利用频率估计概率
19.【答案】(1)
(2)解:根据题意,得,
解得,
经检验,是分式方程的解,
.
【知识点】利用频率估计概率;概率公式
20.【答案】(1)折线统计图;(2)0.6,0.4;(3)24只.
【知识点】利用频率估计概率
21.【答案】(1)0.5;0.5
(2)解:40×0.5=20(个),40-20=20(个);
答:估算盒子里白、黑两种颜色的球分别有20个、20个;
(3)解:设需要往盒子里再放入x个白球;
根据题意得:
,
解得:x=10;
经检验x=10是原方程的根,也符合题意,
∴需要往盒子里再放入10个白球.
【知识点】频数(率)分布折线图;利用频率估计概率;概率公式
22.【答案】解:(Ⅰ)∵ = =63,
∴s甲2= ×[(63﹣63)2×2+(66﹣63)2+2×(61﹣63)2+(64﹣63)2]=3;
∵ = =63,
∴s乙2= ×[(63﹣63)2×3+(65﹣63)2+(60﹣63)2+(64﹣63)2]= ,
∵s乙2<s甲2,
∴乙种小麦的株高长势比较整齐;
(Ⅱ)列表如下:
63 66 63 61 64 61
63 63、63 66、63 63、63 61、63 64、63 61、63
65 63、65 66、65 63、65 61、65 64、65 61、65
60 63、60 66、60 63、60 61、60 64、60 61、60
63 63、63 66、63 63、63 61、63 64、63 61、63
64 63、64 66、64 63、64 61、64 64、64 61、64
63 63、63 66、63 63、63 61、63 64、63 61、63
由表格可知,共有36种等可能结果,其中两株配对小麦株高恰好都等于各自平均株高的有6种,
∴所抽取的两株配对小麦株高恰好都等于各自平均株高的概率为 = .
【知识点】用列表法或树状图法求概率;模拟实验;方差
21世纪教育网(www.21cnjy.com)
2 / 9
25.3 用频率估计概率
一、单选题
1.(2019九上·城固期中)已知不透明的袋中只装有黑、白两种球,这些球除颜色外都相同,其中白球有2个,黑球有n个.随机地从袋子中摸出一个球,记录下颜色后,放回袋子中并摇匀.经过大量重复试验发现摸出白球的频率稳定在0.4附近,则n的值为( )
A.2 B.3 C.4 D.5
2.(2024七上·深圳期末)在“世界无烟日”来临之际,小明和他的同学为了解某街道大约有多少成年人吸烟,于是随机调查了该街道个成年人,结果有个成年人吸烟.对于这个数据的收集与处理过程,下列说法正确的是( )
A.调查的方式是普查 B.该街道约有的成年人吸烟
C.该街道只有个成年人不吸烟 D.样本是个吸烟的成年人
3.(2024七下·利津期末)下列说法合理的是( )
A.某彩票的中奖机会是,那么如果买100张彩票一定会有3张中奖
B.在一次课堂进行的实验中,甲、乙两组同学估计硬币落地后,正面朝上的频率分别为和
C.抛掷一枚正六面体骰子,出现2的概率是的意思是,每6次就有1次掷得2
D.任意画一个三角形,其内角和是是随机事件
4.(2024九上·大东月考)在一个不透明的纸箱中,内有蓝色、红色的玻璃球共16个,这些玻璃球除颜色外都相同.小何每次摸出一个球后放回,通过多次摸球试验后发现摸到蓝色玻璃球的频率稳定在,则纸箱中红色玻璃球很可能有( )
A.4个 B.8个 C.12个 D.16个
5.(2021九上·皇姑月考)一个口袋中有红球、白球共10个,这些球除颜色外都相同,将口袋中的球搅拌均匀,从中随机模出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有78次摸到红球,则口袋中白球的个数大约有( )
A.7个 B.8个 C.2个 D.3个
6.在一个不透明的口袋中放着红色、黑色、黄色的橡皮球共有30个,它们除颜色外其它全相同.小刚通过多次摸球试验后发现从中摸到红色球或黄色球的频率稳定在0.15和0.45之间,则口袋中黑色球的个数可能是 ( )
A.14 B.20 C.9 D.6
7.(2019九上·望城期中)下表记录了一名球员在罚球线上罚篮的结果:
投篮次数n 100 150 300 500 800 1000
投中次数m 58 96 17.4 302 484 601
投中频率n/m 0.580 0.640 0.580 0.604 0.605 0.601
这名球员投篮一次,投中的概率约是( )
A.0.58 B.0.6 C.0.64 D.0.55
8.(2020九上·河口期末)小张承包了一片荒山,他想把这片荒山改造成一个橡胶园,现在有一种橡胶树树苗,它的成活率如下表所示,则下面推断中,其中合理的是( ).
移植棵数 成活数 成活率 移植棵数 成活数 成活率
50 47 1500 1335
270 235 3500 3203
400 369 0.923 7000 6335
750 662 14000 12628
下面有四个推断:
①小张移植3500棵这种树苗,成活率肯定高于 ;②随着移植棵数的增加,树苗成活的频率总在 附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是 ;③若小张移植10000棵这种树苗,则可能成活9000棵;④若小张移植20000棵这种树苗,则一定成活率18000棵.
A.①② B.①④ C.②③ D.②④
9.在一个暗箱里放有x个除颜色外其它完全相同的球,这x个球中白球只有5个.每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到白球的频率稳定在20%,那么可以推算出x大约是( )
A.20 B.25 C.30 D.40
10.(2025八下·沛县月考)如图1所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为,宽为的长方形,将不规则图案围起来,然后在适当位置随机朝长方形区域扔小球,并记录小球落在不规则图案上的次数(小球扔在界线上或长方形区域外不计入试验结果),他将若干次有效试验的结果绘制成了图2所示的折线统计图,由此可估计不规则图案的面积大约是( )
A. B. C. D.
二、填空题
11.(2024九上·拱墅月考)某学习小组做“用频率估计概率”的试验时,计算了某一结果出现的频率,并绘制了表格,则该结果发生的概率约为 (精确到0.01).
试验次数 100 500 1000 2000 4000
频率 0.37 0.32 0.34 0.339 0.333
12.(2023九上·绍兴期中)在一个不透明的袋子中有若千个小球,这些球除颜色外无其他差别,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,然后把它重新放回袋中并摇匀,不断重复上述过程.以下是利用计算机模拟的摸球试验统计表:
摸球实验次数 100 1000 5000 10000 50000 100000
“摸出黑球”的次数 36 387 2019 4009 19970 40008
“摸出黑球”的频率 (结果保留小数点后三位) 0.360 0.387 0.404 0.401 0.399 0.400
根据试验所得数据,估计“摸出黑球”的概率是 (结果保留小数点后一位).
13.(2021九上·南召期末)林业部门要考察某种幼树在一定条件下的移植成活率,下表是这种幼树在移植过程中的一组数据:
移植的棵数n 1000 1500 2500 4000 8000 15000 20000 30000
成活的棵数m 865 1356 2220 3500 7056 13170 17580 26430
成活的频率 0.865 0.904 0.888 0.875 0.882 0.878 0.879 0.881
估计该种幼树在此条件下移植成活的概率为 .
14.(2024九上·重庆市开学考)一个不透明的箱子里装有n个球,其中红球有5个,这些球除颜色外都相同.每次将球搅拌均匀后,任意摸出一个球记下颜色后再放回.大量重复试验后发现,摸到红球的频率稳定在0.25,那么可以估算出n的值为 .
15.(2023九上·新罗月考)某林业部门要考察某种幼树在一定条件下的移植成活率,在同样条件下,对这种幼树进行大量移植,并完成统计情况,得到一组统计数据:
移植总次数n 1500 3500 7000 9000 14000
成活数m 1335 3203 6335 8037 12628
成活的频率
估计该种幼树在此条件下移植成活的概率是 (结果精确到0.1).
16.(2025九上·清新期末)一口袋中有6个红球和若干个白球,除颜色外均相同,从口袋中随机摸出一球,记下颜色,再把它放回口袋中摇匀.重复上述实验共300次,其中120次摸到红球,则口袋中大约有 个白球.
三、计算题
17.(2024九上·余杭月考)某校生物兴趣小组在相同的试验条件下,对某植物种子发芽率进行试验研究时,收集的试验结果如表所示:
试验的种子粒数(n) 500 1000 1500 2000 3000 4000
发芽的种子粒数(m) 471 946 1425 1898 2853 3812
发芽频率 x
(1)求表中x的值;
(2)任取一粒这种植物的种子,请你估计它能发芽的概率(精确到);
(3)若该学校劳动基地需要这种植物幼苗7600株,试估算该小组至少需要准备多少粒种子进行发芽培育.
18.(2024七下·贵阳月考)研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,记录球的颜色,放回盒中,然后重复上述过程.
活动结果:摸球实验活动一共做了50次,统计结果如下表:
球的颜色 无记号 有记号
红色 黄色 红色 黄色
摸到的次数 18 28 2 2
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
四、解答题
19.(2024九上·白银期末)在一个不透明的箱子中装有形状、大小均一样的小球,其中红色小球有3个,白色小球有1个.
(1)小远从箱子中任意摸出1个小球,则刚好摸出白色小球的概率为________.
(2)小远将前面摸出的1个小球放回箱子,又放入个白色小球,摇晃均匀后任意摸出1个小球,记下颜色,经过大量反复的试验,发现摸到白色小球的概率约为,求的值.
20.(2024八下·泗阳期中)在一个不透明的布袋中装有黄、白两种颜色的球共40只,这些球除颜色外其余均相同.小红按如下规则做摸球实验:将这些球搅匀后从中随机摸出一只球,记下颜色后再把球放回布袋中,不断重复上述过程. 下表是实验得到的一组统计数据:
摸球的次数 50 100 200 300 500 1 000 2000 3 000
摸到黄球的频数 36 67 128 176 306 593 1256 1803
摸到黄球的频率 0.72 0.67 0.64 0.59 0.61 0.59 0.63 0.60
(1)对实验得到的数据,选用“扇形统计图”、“条形统计图”或“折线统计图”中的 (填
写一种),能使我们更好地观察摸到黄球频率的变化情况;
(2)请估计:①当摸球次数很大时,摸到黄球的频率将会接近 ;(精确到0.1)
②若从布袋中随机摸出一只球,则摸到白球的概率为 ;(精确到0.1)
(3)试估算布袋中黄球的只数.
21.在一个不透明的盒子里装有黑、白两种颜色的球共40个,小颖做摸球试验.她将盒子里面的球搅匀后从中随机摸出一个球,记下颜色,然后把它放回盒子中.不断重复上述过程.如图所示为“摸到白球”的频率折线统计图.
(1)请估计:当n足够大时,摸到白球的频率将会接近 (结果精确到0.1),假如你摸一次,你摸到白球的概率为
(2)试估算盒子里白、黑两种颜色的球各有多少个.
(3)在(2)的条件下,如果要使摸到白球的频率稳定在,需要往盒子里再放入多少个白球?
22.(2017·滨州)为了考察甲、乙两种成熟期小麦的株高长势情况,现从中随机抽取6株,并测得它们的株高(单位:cm)如下表所示:
甲 63 66 63 61 64 61
乙 63 65 60 63 64 63
(Ⅰ)请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐?
(Ⅱ)现将进行两种小麦优良品种杂交实验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对情况,请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
答案解析部分
1.【答案】B
【知识点】利用频率估计概率
2.【答案】B
【知识点】全面调查与抽样调查;总体、个体、样本、样本容量;用样本估计总体;利用频率估计概率
3.【答案】B
【知识点】可能性的大小;概率的意义;利用频率估计概率;概率公式
4.【答案】C
【知识点】利用频率估计概率
5.【答案】C
【知识点】利用频率估计概率
6.【答案】B
【知识点】利用频率估计概率
7.【答案】B
【知识点】利用频率估计概率
8.【答案】C
【知识点】利用频率估计概率
9.【答案】B
【知识点】利用频率估计概率
10.【答案】B
【知识点】几何概率;利用频率估计概率
11.【答案】0.33
【知识点】利用频率估计概率
12.【答案】0.4
【知识点】利用频率估计概率
13.【答案】0.880
【知识点】利用频率估计概率
14.【答案】20
【知识点】利用频率估计概率
15.【答案】0.9
【知识点】利用频率估计概率
16.【答案】9
【知识点】利用频率估计概率
17.【答案】(1)
(2)
(3)
【知识点】利用频率估计概率
18.【答案】(1)红球占40%,黄球占60%;(2)盒中红球有40个.
【知识点】利用频率估计概率
19.【答案】(1)
(2)解:根据题意,得,
解得,
经检验,是分式方程的解,
.
【知识点】利用频率估计概率;概率公式
20.【答案】(1)折线统计图;(2)0.6,0.4;(3)24只.
【知识点】利用频率估计概率
21.【答案】(1)0.5;0.5
(2)解:40×0.5=20(个),40-20=20(个);
答:估算盒子里白、黑两种颜色的球分别有20个、20个;
(3)解:设需要往盒子里再放入x个白球;
根据题意得:
,
解得:x=10;
经检验x=10是原方程的根,也符合题意,
∴需要往盒子里再放入10个白球.
【知识点】频数(率)分布折线图;利用频率估计概率;概率公式
22.【答案】解:(Ⅰ)∵ = =63,
∴s甲2= ×[(63﹣63)2×2+(66﹣63)2+2×(61﹣63)2+(64﹣63)2]=3;
∵ = =63,
∴s乙2= ×[(63﹣63)2×3+(65﹣63)2+(60﹣63)2+(64﹣63)2]= ,
∵s乙2<s甲2,
∴乙种小麦的株高长势比较整齐;
(Ⅱ)列表如下:
63 66 63 61 64 61
63 63、63 66、63 63、63 61、63 64、63 61、63
65 63、65 66、65 63、65 61、65 64、65 61、65
60 63、60 66、60 63、60 61、60 64、60 61、60
63 63、63 66、63 63、63 61、63 64、63 61、63
64 63、64 66、64 63、64 61、64 64、64 61、64
63 63、63 66、63 63、63 61、63 64、63 61、63
由表格可知,共有36种等可能结果,其中两株配对小麦株高恰好都等于各自平均株高的有6种,
∴所抽取的两株配对小麦株高恰好都等于各自平均株高的概率为 = .
【知识点】用列表法或树状图法求概率;模拟实验;方差
21世纪教育网(www.21cnjy.com)
2 / 9
同课章节目录
