【核心考点集训】第五单元《认识方程》学案--北师大版四年级下册
文档属性
| 名称 | 【核心考点集训】第五单元《认识方程》学案--北师大版四年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 736.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
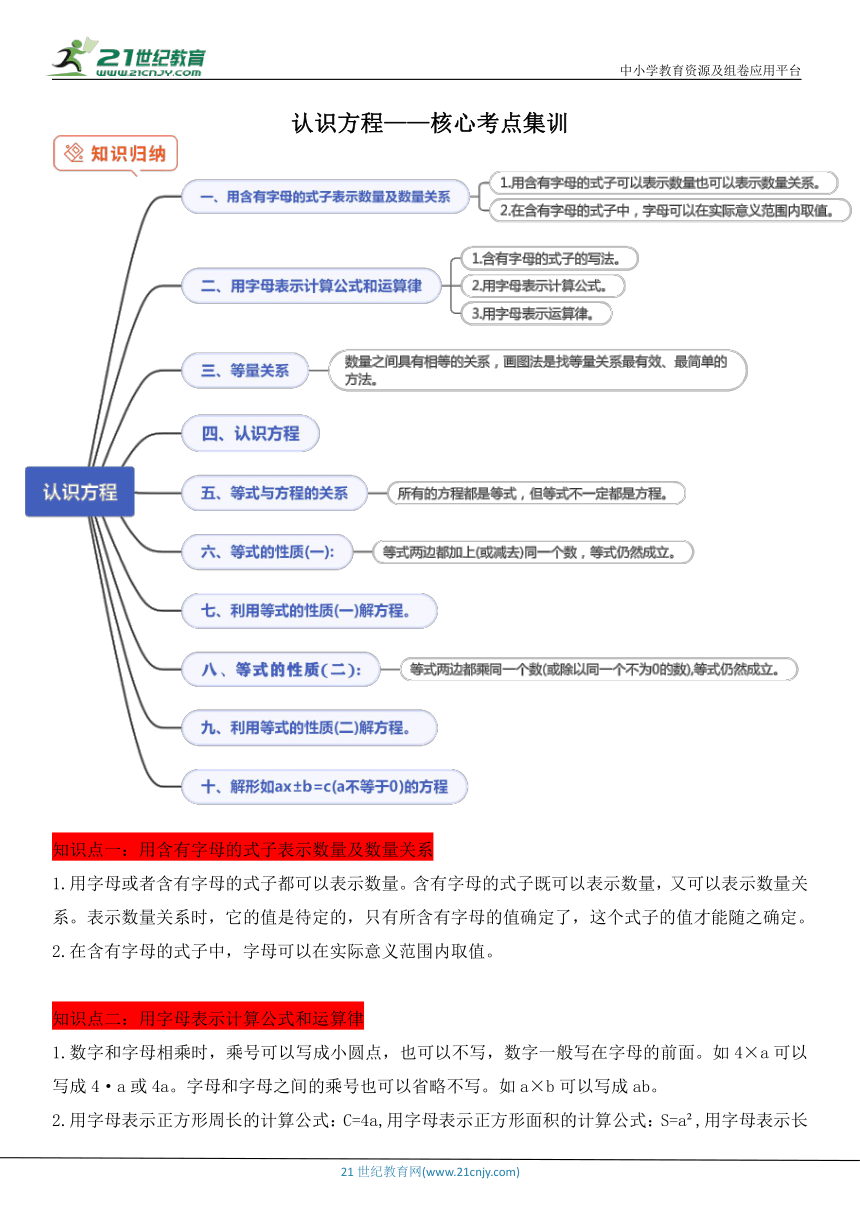
认识方程——核心考点集训
知识点一:用含有字母的式子表示数量及数量关系
1.用字母或者含有字母的式子都可以表示数量。含有字母的式子既可以表示数量,又可以表示数量关系。表示数量关系时,它的值是待定的,只有所含有字母的值确定了,这个式子的值才能随之确定。
2.在含有字母的式子中,字母可以在实际意义范围内取值。
知识点二:用字母表示计算公式和运算律
1.数字和字母相乘时,乘号可以写成小圆点,也可以不写,数字一般写在字母的前面。如4×a可以写成4·a或4a。字母和字母之间的乘号也可以省略不写。如a×b可以写成ab。
2.用字母表示正方形周长的计算公式:C=4a,用字母表示正方形面积的计算公式:S=a ,用字母表示长方形周长的计算公式:C=2(a+b),用字母表示长方形面积的计算公式:S=ab。
3.通常用固定的字母表示运算律。用字母表示运算律更简便易记。
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
乘法交换律:axb=b×a或ab=ba
乘法结合律:(a×b)×c=ax(b×c)或(ab)c=a(bc)
乘法分配律:(a+b)xc=axc+b×c或(a+b)c=ac+bc
知识点三:等量关系
等量关系是指数量之间具有的相等关系。寻找等量关系的方法有很多,画图是最有效、最直观的方法。
知识点四:认识方程
1.像10=x+2,4y=2000,…这样含有未知数的等式叫方程。
2.所有的方程都是等式,但等式不一定都是方程。
知识点五:解方程
解方程(一)
1.等式两边都加上(或减去)同一个数,等式仍然成立。
2.方程的解:使方程左右两边相等的未知数的值,叫作方程的解。
3.解方程:求方程的解的过程叫作解方程。
4.检验方程的步骤:(1)把求出的未知数的值代入原方程中。(2)计算,看等式是否成立。(3)等式成立,说明这个未知数的值是方程的解;等式不成立,说明计算错误,需要重新计算。
解方程(二)
1.等式两边都乘同一个数(或除以同一个不为0的数),等式仍然成立。
2.利用等式的性质(二)解方程。
解形如“ax±b=c(a不等于0)”的方程
解形如“ax±b=c(a不等于0)”这样的方程也要根据等式的性质,具体步骤如下:
ax+b=c ax-b=c
解:ax=c-b 解:ax=c+b
x=(c-b)÷a x=(c+b)÷a
【典例1】用含有字母的式子表示图形中的规律
看图回答问题。(图中小正方形的边长为a厘米)
(1)1个小正方形的周长是( )厘米,2个小正方形拼成一个长方形的周长是( )厘米。
(2)n个小正方形拼成一个长方形的周长是( )厘米。
【典例2】根据数量关系列方程
用方程表示下面各题中的数量关系。
(1)张老师把a本作业本平均分给45名同学,每人分2本正好分完。
(2)8名同学一起去植物园参观,每张门票x元,他们带了100元,找回20元。
【典例3】根据等式的性质求算式中未知数的值
已知a+b+c=33,a+a+b=31,a+b-c=9,求a、b、c各是多少。
【典例4】用方程解决应用题
1.乙粮仓原来有一些粮食,甲粮仓有5000吨粮食,运到乙粮仓1800吨后,甲、乙粮仓的粮食同样多。乙原来有多少粮食?
2.哥哥收集了34张卡片,哥哥收集的卡片数量比弟弟收集数量的3倍多4张,弟弟收集了多少张卡片
3.甲、乙两艘货轮同时从泉州开往上海,经过6小时,甲货轮落后乙货轮42千米。甲货轮每小时行25千米,乙货轮每小时行多少千米
1.像这样摆下去, 摆5个三角形需要( )根小棒,摆n个三角形需要( )根小棒。摆15个三角形需要( )根小棒。
2.根据数量关系列方程。
(1)小明带了x元去书店买书,一本故事书花了9元,还剩下16元。用方程表示为( )。
(2)小明的身高是m厘米,爸爸的身高比小明身高的2倍少90米,爸爸的身高是180厘米。
用方程表示为( )。
3.如果a+a+a+b+b=54,a+a+b+b=46,那么a和b各是多少
4.红红有15本故事书,如果红红送给丽丽3本故事书,两人的故事书就同样多了。丽丽有多少本故事书?
5.春季植树活动,第一组植树256棵,比第二组植树棵数的3倍少20棵。第二组植树多少棵
6.黑马和白马在相距50米的地方同时出发,同向而行。出发时黑马在前,白马在后。如果黑马每秒跑10米,白马每秒跑12米,经过多少秒两马相距70米
参考答案
【典例1】用含有字母的式子表示图形中的规律
看图回答问题。(图中小正方形的边长为a厘米)
(1)1个小正方形的周长是( 4a )厘米,2个小正方形拼成一个长方形的周长是( 6a )厘米。
(2)n个小正方形拼成一个长方形的周长是( 2a×(n+1) )厘米。
【典例2】根据数量关系列方程
用方程表示下面各题中的数量关系。
(1)张老师把a本作业本平均分给45名同学,每人分2本正好分完。
(2)8名同学一起去植物园参观,每张门票x元,他们带了100元,找回20元。
(1)a÷45=2
(2)100-8x=20
【典例3】根据等式的性质求算式中未知数的值
已知a+b+c=33,a+a+b=31,a+b-c=9,求a、b、c各是多少。
【典例4】用方程解决应用题
1.乙粮仓原来有一些粮食,甲粮仓有5000吨粮食,运到乙粮仓1800吨后,甲、乙粮仓的粮食同样多。乙原来有多少粮食?
2.哥哥收集了34张卡片,哥哥收集的卡片数量比弟弟收集数量的3倍多4张,弟弟收集了多少张卡片
3.甲、乙两艘货轮同时从泉州开往上海,经过6小时,甲货轮落后乙货轮42千米。甲货轮每小时行25千米,乙货轮每小时行多少千米
1.像这样摆下去, 摆5个三角形需要( 11 )根小棒,摆n个三角形需要( 2n+1 )根小棒。摆15个三角形需要( 31 )根小棒。
2.根据数量关系列方程。
(1)小明带了x元去书店买书,一本故事书花了9元,还剩下16元。用方程表示为(x-9=16 )。
(2)小明的身高是m厘米,爸爸的身高比小明身高的2倍少90米,爸爸的身高是180厘米。
用方程表示为( 2m-90=180 )。
3.如果a+a+a+b+b=54,a+a+b+b=46,那么a和b各是多少
4.红红有15本故事书,如果红红送给丽丽3本故事书,两人的故事书就同样多了。丽丽有多少本故事书?
5.春季植树活动,第一组植树256棵,比第二组植树棵数的3倍少20棵。第二组植树多少棵
6.黑马和白马在相距50米的地方同时出发,同向而行。出发时黑马在前,白马在后。如果黑马每秒跑10米,白马每秒跑12米,经过多少秒两马相距70米
21世纪教育网(www.21cnjy.com)
认识方程——核心考点集训
知识点一:用含有字母的式子表示数量及数量关系
1.用字母或者含有字母的式子都可以表示数量。含有字母的式子既可以表示数量,又可以表示数量关系。表示数量关系时,它的值是待定的,只有所含有字母的值确定了,这个式子的值才能随之确定。
2.在含有字母的式子中,字母可以在实际意义范围内取值。
知识点二:用字母表示计算公式和运算律
1.数字和字母相乘时,乘号可以写成小圆点,也可以不写,数字一般写在字母的前面。如4×a可以写成4·a或4a。字母和字母之间的乘号也可以省略不写。如a×b可以写成ab。
2.用字母表示正方形周长的计算公式:C=4a,用字母表示正方形面积的计算公式:S=a ,用字母表示长方形周长的计算公式:C=2(a+b),用字母表示长方形面积的计算公式:S=ab。
3.通常用固定的字母表示运算律。用字母表示运算律更简便易记。
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
乘法交换律:axb=b×a或ab=ba
乘法结合律:(a×b)×c=ax(b×c)或(ab)c=a(bc)
乘法分配律:(a+b)xc=axc+b×c或(a+b)c=ac+bc
知识点三:等量关系
等量关系是指数量之间具有的相等关系。寻找等量关系的方法有很多,画图是最有效、最直观的方法。
知识点四:认识方程
1.像10=x+2,4y=2000,…这样含有未知数的等式叫方程。
2.所有的方程都是等式,但等式不一定都是方程。
知识点五:解方程
解方程(一)
1.等式两边都加上(或减去)同一个数,等式仍然成立。
2.方程的解:使方程左右两边相等的未知数的值,叫作方程的解。
3.解方程:求方程的解的过程叫作解方程。
4.检验方程的步骤:(1)把求出的未知数的值代入原方程中。(2)计算,看等式是否成立。(3)等式成立,说明这个未知数的值是方程的解;等式不成立,说明计算错误,需要重新计算。
解方程(二)
1.等式两边都乘同一个数(或除以同一个不为0的数),等式仍然成立。
2.利用等式的性质(二)解方程。
解形如“ax±b=c(a不等于0)”的方程
解形如“ax±b=c(a不等于0)”这样的方程也要根据等式的性质,具体步骤如下:
ax+b=c ax-b=c
解:ax=c-b 解:ax=c+b
x=(c-b)÷a x=(c+b)÷a
【典例1】用含有字母的式子表示图形中的规律
看图回答问题。(图中小正方形的边长为a厘米)
(1)1个小正方形的周长是( )厘米,2个小正方形拼成一个长方形的周长是( )厘米。
(2)n个小正方形拼成一个长方形的周长是( )厘米。
【典例2】根据数量关系列方程
用方程表示下面各题中的数量关系。
(1)张老师把a本作业本平均分给45名同学,每人分2本正好分完。
(2)8名同学一起去植物园参观,每张门票x元,他们带了100元,找回20元。
【典例3】根据等式的性质求算式中未知数的值
已知a+b+c=33,a+a+b=31,a+b-c=9,求a、b、c各是多少。
【典例4】用方程解决应用题
1.乙粮仓原来有一些粮食,甲粮仓有5000吨粮食,运到乙粮仓1800吨后,甲、乙粮仓的粮食同样多。乙原来有多少粮食?
2.哥哥收集了34张卡片,哥哥收集的卡片数量比弟弟收集数量的3倍多4张,弟弟收集了多少张卡片
3.甲、乙两艘货轮同时从泉州开往上海,经过6小时,甲货轮落后乙货轮42千米。甲货轮每小时行25千米,乙货轮每小时行多少千米
1.像这样摆下去, 摆5个三角形需要( )根小棒,摆n个三角形需要( )根小棒。摆15个三角形需要( )根小棒。
2.根据数量关系列方程。
(1)小明带了x元去书店买书,一本故事书花了9元,还剩下16元。用方程表示为( )。
(2)小明的身高是m厘米,爸爸的身高比小明身高的2倍少90米,爸爸的身高是180厘米。
用方程表示为( )。
3.如果a+a+a+b+b=54,a+a+b+b=46,那么a和b各是多少
4.红红有15本故事书,如果红红送给丽丽3本故事书,两人的故事书就同样多了。丽丽有多少本故事书?
5.春季植树活动,第一组植树256棵,比第二组植树棵数的3倍少20棵。第二组植树多少棵
6.黑马和白马在相距50米的地方同时出发,同向而行。出发时黑马在前,白马在后。如果黑马每秒跑10米,白马每秒跑12米,经过多少秒两马相距70米
参考答案
【典例1】用含有字母的式子表示图形中的规律
看图回答问题。(图中小正方形的边长为a厘米)
(1)1个小正方形的周长是( 4a )厘米,2个小正方形拼成一个长方形的周长是( 6a )厘米。
(2)n个小正方形拼成一个长方形的周长是( 2a×(n+1) )厘米。
【典例2】根据数量关系列方程
用方程表示下面各题中的数量关系。
(1)张老师把a本作业本平均分给45名同学,每人分2本正好分完。
(2)8名同学一起去植物园参观,每张门票x元,他们带了100元,找回20元。
(1)a÷45=2
(2)100-8x=20
【典例3】根据等式的性质求算式中未知数的值
已知a+b+c=33,a+a+b=31,a+b-c=9,求a、b、c各是多少。
【典例4】用方程解决应用题
1.乙粮仓原来有一些粮食,甲粮仓有5000吨粮食,运到乙粮仓1800吨后,甲、乙粮仓的粮食同样多。乙原来有多少粮食?
2.哥哥收集了34张卡片,哥哥收集的卡片数量比弟弟收集数量的3倍多4张,弟弟收集了多少张卡片
3.甲、乙两艘货轮同时从泉州开往上海,经过6小时,甲货轮落后乙货轮42千米。甲货轮每小时行25千米,乙货轮每小时行多少千米
1.像这样摆下去, 摆5个三角形需要( 11 )根小棒,摆n个三角形需要( 2n+1 )根小棒。摆15个三角形需要( 31 )根小棒。
2.根据数量关系列方程。
(1)小明带了x元去书店买书,一本故事书花了9元,还剩下16元。用方程表示为(x-9=16 )。
(2)小明的身高是m厘米,爸爸的身高比小明身高的2倍少90米,爸爸的身高是180厘米。
用方程表示为( 2m-90=180 )。
3.如果a+a+a+b+b=54,a+a+b+b=46,那么a和b各是多少
4.红红有15本故事书,如果红红送给丽丽3本故事书,两人的故事书就同样多了。丽丽有多少本故事书?
5.春季植树活动,第一组植树256棵,比第二组植树棵数的3倍少20棵。第二组植树多少棵
6.黑马和白马在相距50米的地方同时出发,同向而行。出发时黑马在前,白马在后。如果黑马每秒跑10米,白马每秒跑12米,经过多少秒两马相距70米
21世纪教育网(www.21cnjy.com)
