2026年中考《数学》复习课件:专题二 方程(组)与不等式(组)-第7讲 分式方程(42张PPT)
文档属性
| 名称 | 2026年中考《数学》复习课件:专题二 方程(组)与不等式(组)-第7讲 分式方程(42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 07:07:30 | ||
图片预览











文档简介
(共42张PPT)
复习讲义
第一篇 吃透考点
专题二 方程(组)与不等式(组)
第7讲 分式方程
聚焦核心
1.分式方程的定义
______中含有未知数的方程叫作分式方程.
分母
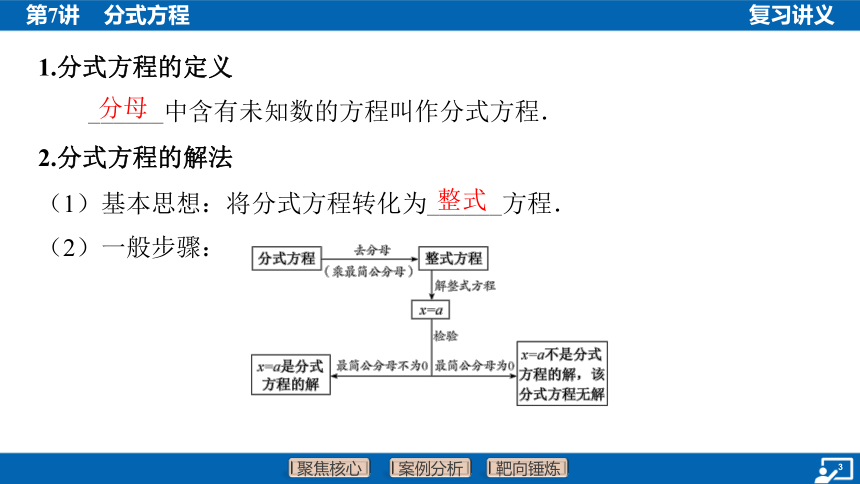
2.分式方程的解法
(1)基本思想:将分式方程转化为______方程.
(2)一般步骤:
整式
第7讲 分式方程
案例分析
考点一 分式方程的解法
名师指导
1.正确找到最简公分母是解分式方程的关键,找到最简公分母之前,
要把各分母中能因式分解的先因式分解,然后在方程两边同时乘最简公
分母(最简公分母要乘方程的每一项,不要漏乘),把分式方程转化为
整式方程求解.
2.解分式方程后要进行检验,即把求出的未知数的值代入最简公分
母.若它使最简公分母的值不为0,则是原分式方程的解;若它使最简公
分母的值为0,则不是原分式方程的解,原分式方程无解.
例1 (2025·汉中·中考模拟)解分式方程: .
思路点拨 根据解分式方程的一般步骤进行计算.
易错提醒:(1)去分母时,不要弄错符号,不要漏乘没有分母的项;
(2)不要忘记验根.
解:去分母,得.
去括号,得.
移项、合并同类项,得.
检验:当时,.
所以原分式方程的解为.
考点专练
1.(2024·广东·中考)方程 的解为( ).
C
A. B. C. D.
2.解分式方程:
(1)(2025·广西北海·模拟) ;
解:去分母,得.
移项,得.
所以.检验:当时,.
所以原分式方程的解为.
(2) ;
解:去分母,得.
移项、合并同类项,得.
所以.
检验:当时,.
所以原分式方程无解.
(3)(2025·莆田·中考模拟) .
解:去分母,得,即3.
所以.检验:当时,.
所以原分式方程的解为.
考点二 根据分式方程的解的情况求未知系数的值或取值范围
名师指导
1.当分式方程有解时,求未知系数取值范围的一般步骤:(1)解
分式方程,根据解的取值范围列出关于未知系数的不等式,解不等式得
到未知系数的取值范围;(2)舍去使分式方程无解的未知系数的值,
得出满足题目条件的未知系数的取值范围.
2.分式方程无解通常有以下两种情况:
(1)去分母后化成的整式方程有解,但这个解使原方程的最简公
分母为0;(2)去分母后化成的整式方程无解,如关于的方程 ,
当, 时,这个方程无解.
例2 (2025·四川遂宁·中考模拟)已知关于的分式方程 的解为
正数,则 的取值范围是( ).
A. B.且
C. D.且
思路点拨 用含 的式子表示出分式方程的解,再根据分式方程的解为
正数,且最简公分母不为0,就可以求出 的取值范围.
提示:方程两边同时乘,得.解得 .因为分
式方程的解为正数,所以.所以 .由
,得,即,所以.所以 的取值范围为
且 .
【答案】B
考点专练
3.(2024·山东淄博·中考)已知是方程 的解,那么实
数 的值为( ).
B
A. B.2 C. D.4
4.(2025·黑龙江牡丹江·中考模拟)若分式方程 的解为正整数,
则整数 的值为____.
提示:方程两边同时乘,得 .整理得
.解得.因为原方程有解,所以,即 ,
且.所以且.由原方程的解是正整数,且 为整数,
得或.解得或 (舍去).
5.(2024·四川达州·中考模拟)若关于的方程无解,则 的值
为_______.
或2
提示:方程两边同时乘,得 .整理得
.解得.因为原方程无解,所以或 .解
得或 .
考点三 分式方程的应用
名师指导
对于分式方程的应用问题,要注意对求出的未知数的值进行“双检
验”:
(1)检验是不是分式方程的解;
(2)检验是不是符合题意.
例3 (2024·广西河池·模拟)某汽车制造厂接到两项都为生产360辆汽车
的任务.
(1)完成第一项任务时,生产的第一天按原计划的生产速度进行,第
一天后按原计划生产速度的1.5倍进行,结果提前3天完成任务,问完成
第一项任务实际需要多少天?
思路点拨(1)本题的等量关系是“计划完成的天数 提高效率后生产的天数 ”.
解:设原计划每天生产辆,则第二天开始每天生产 辆.
由题意,得.解得.
经检验, 是原分式方程的解,且符合题意.所以 .
答:完成第一项任务实际需要7天.
(2)在完成第二项任务时,制造厂设计了甲、乙两个不同的生产方案
(其中 ).
甲方案:计划180辆按每天生产辆完成,剩下的180辆按每天生产
辆完成,设完成生产任务所需的时间为 天.
乙方案:计划一半时间每天生产辆,另一半时间每天生产 辆,设
完成生产任务所需的时间为 天.
请比较, 的大小,并说明理由.
思路点拨(2)用含,的代数式表示, ,再用作差法比较大小.
解:.
理由:对于甲方案,(天);对于乙方案,,解得.
.
因为,,,所以
,.
所以.
所以.
考点专练
6.(2024·广西南宁·模拟)甲、乙两人每天骑自行车出行,甲匀速骑行
的时间与乙匀速骑行 的时间相同,已知甲每小时比乙每小
时多骑行,设甲每小时骑行 ,根据题意列出的方程正确的是
( ).
C
A. B. C. D.
7.(2025·内蒙古呼和浩特·中考模拟)甲、乙两船从相距 的A,B两地
同时匀速沿江出发相向而行,甲船从A地顺流航行 时与从B地逆流
航行的乙船相遇.甲、乙两船在静水中的航速均为 ,则江水的流
速是___ .
6
提示:设江水的流速为.根据题意,得.解得 .经
检验, 是原分式方程的解,且符合题意.
8.数学文化(2024·江苏常州·中考)书画装裱,
是指为书画配上衬纸、卷轴以便张贴、欣赏和
收藏,是我国一门具有民族传统的独特艺术.如
下图,一幅书画在装裱前的大小是
.装裱后,上、下、左、右边衬的
宽度分别是,,,.若装裱后与的比是 ,且
,, ,求四周边衬的宽度.
解:由题意,得 ,.
因为与 的比是,所以.
解得 .
经检验,是原分式方程的解,且符合题意.
所以 ,.
答:上、下、左、右边衬的宽度分别是, ,0, .
第7讲 分式方程
靶向锤炼
靶向练
1.(2025·山东济宁·中考模拟)解分式方程 时,去分母变形
正确的是( ).
A
A. B.
C. D.
2.(2024·四川德阳·中考模拟)分式方程 的解是( ).
D
A.3 B.2 C. D.
3.(2024·广西南宁·模拟)某工厂现在平均每天比原计划多生产50台机
器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同,
设现在平均每天生产机器 台,根据题意,可列方程为( ).
C
A. B. C. D.
4.(2024·北京·中考)方程 的解为________.
5.解分式方程:
(1)(2024·广东广州·中考) ;
解:去分母,得,即.
所以.
检验:当
时,.
所以原分式方程的解为.
(2) ;
解:去分母,得,即.
所以.
检验:当时,.
所以原分式方程无解.
(3) .
解:去分母,得,即
以.
检验:当x=2时,(x+1)(x 1)≠0.
以原分式方程的解为.
6.(2024·四川自贡·中考)为传承我国传统文化,端午节前夕,某校组
织了包粽子活动.已知甲组同学平均每小时比乙组多包20个粽子,甲组
包150个粽子所用的时间与乙组包120个粽子所用的时间相同.求甲、乙
两组同学平均每小时各包多少个粽子.
解:设乙组平均每小时包个粽子,则甲组平均每小时包 个粽子.
由题意,得.解得
检验, 是原分式方程的解,且符合题意.
所以 .
答:甲组平均每小时包100个粽子,乙组平均每小时包80个粽子.
提分练
7.(2025·黑龙江齐齐哈尔·中考模拟)如果关于的分式方程 的解是
负数,那么实数 的取值范围是( ).
D
A. B.且
C. D.且
8.(2024·黑龙江绥化·中考)某运输公司运送一批货物,甲车每天运送
货物总量的 .在甲车运送1天货物后,公司增派乙车运送货物,两车又共
同运送货物 天,运完全部货物.求乙车单独运送这批货物需多少天.设乙
车单独运送这批货物需 天.根据题意,可列方程为( ).
B
A. B.
C. D.
9.(2024·山东东营·中考)水是人类赖以生存的宝贵资源,为节约用水,
创建文明城市,某市经论证从2024年1月1日起调整居民用水价格,每立
方米水费上涨原价的 .小丽家2023年5月份的水费是28元,而2024年5月
份的水费是24.5元.已知小丽家2024年5月份的用水量比2023年5月份的用
水量少.设该市2023年居民用水价格为元/ ,则可列分式方程为
_ _____________.
10.(2024·内蒙古呼和浩特·中考节选)2024年春晚吉祥物“龙辰辰”,以
十二生肖龙的专属汉字“辰”为名.某厂家生产大小两种型号的“龙辰辰”,
大号“龙辰辰”单价比小号“龙辰辰”单价贵15元,且用2 400元购进小号
“龙辰辰”的数量是用2 200元购进大号“龙辰辰”数量的1.5倍,则大号“龙
辰辰”的单价为 ____元.
提示:设小号“龙辰辰”的单价为元,则大号“龙辰辰”的单价为
元.根据题意,得.解得.经检验, 是原分式
方程的解,且符合题意.所以 ,即大号“龙辰辰”的单价为55元.
55
11.(2024·四川雅安·中考)某市为治理污水,保护环境,需铺设一段全
长为 的污水排放管道,为了减少施工对城市交通所造成的影响,
实际施工时每天的工效(单位时间的施工量)比原计划增加 ,结果
提前15天完成铺设任务.
(1)原计划与实际每天铺设管道各多少米?
解:设原计划每天铺设管道 ,则实际施工每天铺设管道 .
根据题意,得.
解得检验, 是原分式方程的解,且符合题意.
所以.
答:原计划每天铺设管道 ,实际每天铺设管道 .
(2)负责该工程的施工单位按原计划对工人的工资进行了初步预算,
工人每天人均工资为300元,所有工人的工资总金额不超过18万元,该
施工单位原计划最多安排多少名工人施工?
解:设该施工单位原计划安排 名工人施工,则原计划完成铺设任务需(天).
根据题意,得300×75 ≤180 000.
得 .
所以 的最大整数解为8.
则该施工单位原计划最多安排8名工人施工.
拔尖练
12.新定义题对于两个不相等的实数,,我们规定,
表示,中的较小的值,例如, .按照这个规定,方程
, 的解为______.
小锦囊 根据新定义列方程求解.注意,要对和 的大小进行分情况
讨论.
提示:①当时,根据题意,得.解得 .经检
验,是原分式方程的解.此时,, ,所以
不符合题意,舍去.②当时,根据题意,得 .
解得.经检验,是原分式方程的解.此时, ,
,所以符合题意.综上可知,原方程的解为 .
答案
复习讲义
第一篇 吃透考点
专题二 方程(组)与不等式(组)
第7讲 分式方程
聚焦核心
1.分式方程的定义
______中含有未知数的方程叫作分式方程.
分母
2.分式方程的解法
(1)基本思想:将分式方程转化为______方程.
(2)一般步骤:
整式
第7讲 分式方程
案例分析
考点一 分式方程的解法
名师指导
1.正确找到最简公分母是解分式方程的关键,找到最简公分母之前,
要把各分母中能因式分解的先因式分解,然后在方程两边同时乘最简公
分母(最简公分母要乘方程的每一项,不要漏乘),把分式方程转化为
整式方程求解.
2.解分式方程后要进行检验,即把求出的未知数的值代入最简公分
母.若它使最简公分母的值不为0,则是原分式方程的解;若它使最简公
分母的值为0,则不是原分式方程的解,原分式方程无解.
例1 (2025·汉中·中考模拟)解分式方程: .
思路点拨 根据解分式方程的一般步骤进行计算.
易错提醒:(1)去分母时,不要弄错符号,不要漏乘没有分母的项;
(2)不要忘记验根.
解:去分母,得.
去括号,得.
移项、合并同类项,得.
检验:当时,.
所以原分式方程的解为.
考点专练
1.(2024·广东·中考)方程 的解为( ).
C
A. B. C. D.
2.解分式方程:
(1)(2025·广西北海·模拟) ;
解:去分母,得.
移项,得.
所以.检验:当时,.
所以原分式方程的解为.
(2) ;
解:去分母,得.
移项、合并同类项,得.
所以.
检验:当时,.
所以原分式方程无解.
(3)(2025·莆田·中考模拟) .
解:去分母,得,即3.
所以.检验:当时,.
所以原分式方程的解为.
考点二 根据分式方程的解的情况求未知系数的值或取值范围
名师指导
1.当分式方程有解时,求未知系数取值范围的一般步骤:(1)解
分式方程,根据解的取值范围列出关于未知系数的不等式,解不等式得
到未知系数的取值范围;(2)舍去使分式方程无解的未知系数的值,
得出满足题目条件的未知系数的取值范围.
2.分式方程无解通常有以下两种情况:
(1)去分母后化成的整式方程有解,但这个解使原方程的最简公
分母为0;(2)去分母后化成的整式方程无解,如关于的方程 ,
当, 时,这个方程无解.
例2 (2025·四川遂宁·中考模拟)已知关于的分式方程 的解为
正数,则 的取值范围是( ).
A. B.且
C. D.且
思路点拨 用含 的式子表示出分式方程的解,再根据分式方程的解为
正数,且最简公分母不为0,就可以求出 的取值范围.
提示:方程两边同时乘,得.解得 .因为分
式方程的解为正数,所以.所以 .由
,得,即,所以.所以 的取值范围为
且 .
【答案】B
考点专练
3.(2024·山东淄博·中考)已知是方程 的解,那么实
数 的值为( ).
B
A. B.2 C. D.4
4.(2025·黑龙江牡丹江·中考模拟)若分式方程 的解为正整数,
则整数 的值为____.
提示:方程两边同时乘,得 .整理得
.解得.因为原方程有解,所以,即 ,
且.所以且.由原方程的解是正整数,且 为整数,
得或.解得或 (舍去).
5.(2024·四川达州·中考模拟)若关于的方程无解,则 的值
为_______.
或2
提示:方程两边同时乘,得 .整理得
.解得.因为原方程无解,所以或 .解
得或 .
考点三 分式方程的应用
名师指导
对于分式方程的应用问题,要注意对求出的未知数的值进行“双检
验”:
(1)检验是不是分式方程的解;
(2)检验是不是符合题意.
例3 (2024·广西河池·模拟)某汽车制造厂接到两项都为生产360辆汽车
的任务.
(1)完成第一项任务时,生产的第一天按原计划的生产速度进行,第
一天后按原计划生产速度的1.5倍进行,结果提前3天完成任务,问完成
第一项任务实际需要多少天?
思路点拨(1)本题的等量关系是“计划完成的天数 提高效率后生产的天数 ”.
解:设原计划每天生产辆,则第二天开始每天生产 辆.
由题意,得.解得.
经检验, 是原分式方程的解,且符合题意.所以 .
答:完成第一项任务实际需要7天.
(2)在完成第二项任务时,制造厂设计了甲、乙两个不同的生产方案
(其中 ).
甲方案:计划180辆按每天生产辆完成,剩下的180辆按每天生产
辆完成,设完成生产任务所需的时间为 天.
乙方案:计划一半时间每天生产辆,另一半时间每天生产 辆,设
完成生产任务所需的时间为 天.
请比较, 的大小,并说明理由.
思路点拨(2)用含,的代数式表示, ,再用作差法比较大小.
解:.
理由:对于甲方案,(天);对于乙方案,,解得.
.
因为,,,所以
,.
所以.
所以.
考点专练
6.(2024·广西南宁·模拟)甲、乙两人每天骑自行车出行,甲匀速骑行
的时间与乙匀速骑行 的时间相同,已知甲每小时比乙每小
时多骑行,设甲每小时骑行 ,根据题意列出的方程正确的是
( ).
C
A. B. C. D.
7.(2025·内蒙古呼和浩特·中考模拟)甲、乙两船从相距 的A,B两地
同时匀速沿江出发相向而行,甲船从A地顺流航行 时与从B地逆流
航行的乙船相遇.甲、乙两船在静水中的航速均为 ,则江水的流
速是___ .
6
提示:设江水的流速为.根据题意,得.解得 .经
检验, 是原分式方程的解,且符合题意.
8.数学文化(2024·江苏常州·中考)书画装裱,
是指为书画配上衬纸、卷轴以便张贴、欣赏和
收藏,是我国一门具有民族传统的独特艺术.如
下图,一幅书画在装裱前的大小是
.装裱后,上、下、左、右边衬的
宽度分别是,,,.若装裱后与的比是 ,且
,, ,求四周边衬的宽度.
解:由题意,得 ,.
因为与 的比是,所以.
解得 .
经检验,是原分式方程的解,且符合题意.
所以 ,.
答:上、下、左、右边衬的宽度分别是, ,0, .
第7讲 分式方程
靶向锤炼
靶向练
1.(2025·山东济宁·中考模拟)解分式方程 时,去分母变形
正确的是( ).
A
A. B.
C. D.
2.(2024·四川德阳·中考模拟)分式方程 的解是( ).
D
A.3 B.2 C. D.
3.(2024·广西南宁·模拟)某工厂现在平均每天比原计划多生产50台机
器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同,
设现在平均每天生产机器 台,根据题意,可列方程为( ).
C
A. B. C. D.
4.(2024·北京·中考)方程 的解为________.
5.解分式方程:
(1)(2024·广东广州·中考) ;
解:去分母,得,即.
所以.
检验:当
时,.
所以原分式方程的解为.
(2) ;
解:去分母,得,即.
所以.
检验:当时,.
所以原分式方程无解.
(3) .
解:去分母,得,即
以.
检验:当x=2时,(x+1)(x 1)≠0.
以原分式方程的解为.
6.(2024·四川自贡·中考)为传承我国传统文化,端午节前夕,某校组
织了包粽子活动.已知甲组同学平均每小时比乙组多包20个粽子,甲组
包150个粽子所用的时间与乙组包120个粽子所用的时间相同.求甲、乙
两组同学平均每小时各包多少个粽子.
解:设乙组平均每小时包个粽子,则甲组平均每小时包 个粽子.
由题意,得.解得
检验, 是原分式方程的解,且符合题意.
所以 .
答:甲组平均每小时包100个粽子,乙组平均每小时包80个粽子.
提分练
7.(2025·黑龙江齐齐哈尔·中考模拟)如果关于的分式方程 的解是
负数,那么实数 的取值范围是( ).
D
A. B.且
C. D.且
8.(2024·黑龙江绥化·中考)某运输公司运送一批货物,甲车每天运送
货物总量的 .在甲车运送1天货物后,公司增派乙车运送货物,两车又共
同运送货物 天,运完全部货物.求乙车单独运送这批货物需多少天.设乙
车单独运送这批货物需 天.根据题意,可列方程为( ).
B
A. B.
C. D.
9.(2024·山东东营·中考)水是人类赖以生存的宝贵资源,为节约用水,
创建文明城市,某市经论证从2024年1月1日起调整居民用水价格,每立
方米水费上涨原价的 .小丽家2023年5月份的水费是28元,而2024年5月
份的水费是24.5元.已知小丽家2024年5月份的用水量比2023年5月份的用
水量少.设该市2023年居民用水价格为元/ ,则可列分式方程为
_ _____________.
10.(2024·内蒙古呼和浩特·中考节选)2024年春晚吉祥物“龙辰辰”,以
十二生肖龙的专属汉字“辰”为名.某厂家生产大小两种型号的“龙辰辰”,
大号“龙辰辰”单价比小号“龙辰辰”单价贵15元,且用2 400元购进小号
“龙辰辰”的数量是用2 200元购进大号“龙辰辰”数量的1.5倍,则大号“龙
辰辰”的单价为 ____元.
提示:设小号“龙辰辰”的单价为元,则大号“龙辰辰”的单价为
元.根据题意,得.解得.经检验, 是原分式
方程的解,且符合题意.所以 ,即大号“龙辰辰”的单价为55元.
55
11.(2024·四川雅安·中考)某市为治理污水,保护环境,需铺设一段全
长为 的污水排放管道,为了减少施工对城市交通所造成的影响,
实际施工时每天的工效(单位时间的施工量)比原计划增加 ,结果
提前15天完成铺设任务.
(1)原计划与实际每天铺设管道各多少米?
解:设原计划每天铺设管道 ,则实际施工每天铺设管道 .
根据题意,得.
解得检验, 是原分式方程的解,且符合题意.
所以.
答:原计划每天铺设管道 ,实际每天铺设管道 .
(2)负责该工程的施工单位按原计划对工人的工资进行了初步预算,
工人每天人均工资为300元,所有工人的工资总金额不超过18万元,该
施工单位原计划最多安排多少名工人施工?
解:设该施工单位原计划安排 名工人施工,则原计划完成铺设任务需(天).
根据题意,得300×75 ≤180 000.
得 .
所以 的最大整数解为8.
则该施工单位原计划最多安排8名工人施工.
拔尖练
12.新定义题对于两个不相等的实数,,我们规定,
表示,中的较小的值,例如, .按照这个规定,方程
, 的解为______.
小锦囊 根据新定义列方程求解.注意,要对和 的大小进行分情况
讨论.
提示:①当时,根据题意,得.解得 .经检
验,是原分式方程的解.此时,, ,所以
不符合题意,舍去.②当时,根据题意,得 .
解得.经检验,是原分式方程的解.此时, ,
,所以符合题意.综上可知,原方程的解为 .
答案
同课章节目录
