2026年中考《数学》复习课件:专题四 三角形--微专题(六) 与中点有关的模型构造方法(32张PPT)
文档属性
| 名称 | 2026年中考《数学》复习课件:专题四 三角形--微专题(六) 与中点有关的模型构造方法(32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 07:09:30 | ||
图片预览





文档简介
(共32张PPT)
复习讲义
第一篇 考点精讲
专题四 三角形
微专题(六) 与中点有关的模型构造方法
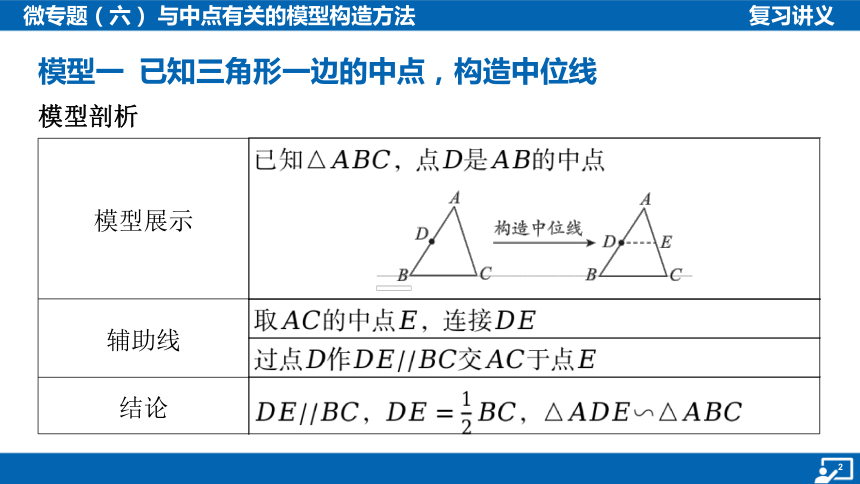
模型一 已知三角形一边的中点,构造中位线
模型剖析
模型展示 已知,点是 的中点
_______________________________________________________________________________
辅助线 取的中点,连接
过点作交于点
结论 ,,
模型应用
图1
1.如图1,在中, ,,
是边的中点,点在边上,若 ,
则 ___.
6
提示:取的中点,连接,则为
的中位线,从而得, .所以
.又 ,所以 .
模型二 已知等腰三角形底边的中点,运用“三线合一”的性质
构造垂直
模型剖析
模型展示 为等腰三角形底边 的中点
_____________________________________
辅助线 连接,则 是顶角的平分线、底边上的中线、底边
上的高(三线合一)
结论 ,平分
模型应用
图2
2.如图2,在中,,,点在
上,且,点,分别是, 的中点,
则 的长是( ).
B
A.3 B.4 C.5 D.6
提示:连接,则 .又是 的中点,
,所以 .
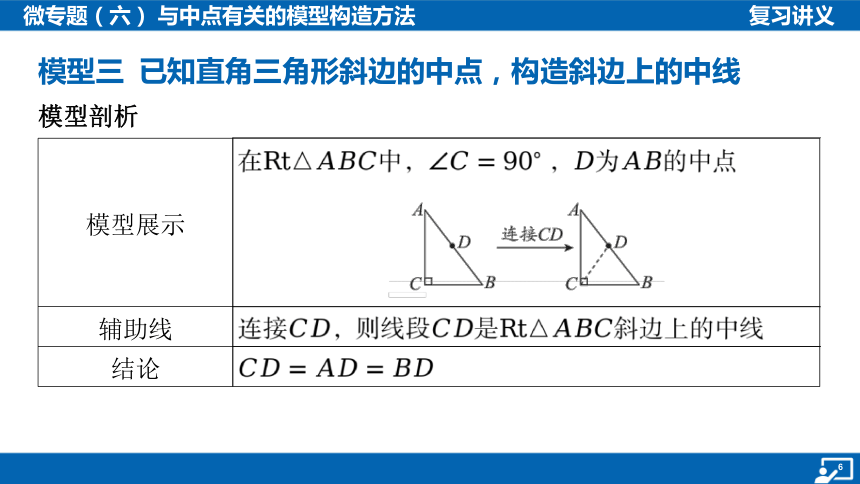
模型三 已知直角三角形斜边的中点,构造斜边上的中线
模型剖析
模型展示 在中, ,为 的中点
_____________________________________________________________________
辅助线 连接,则线段是 斜边上的中线
结论
模型应用
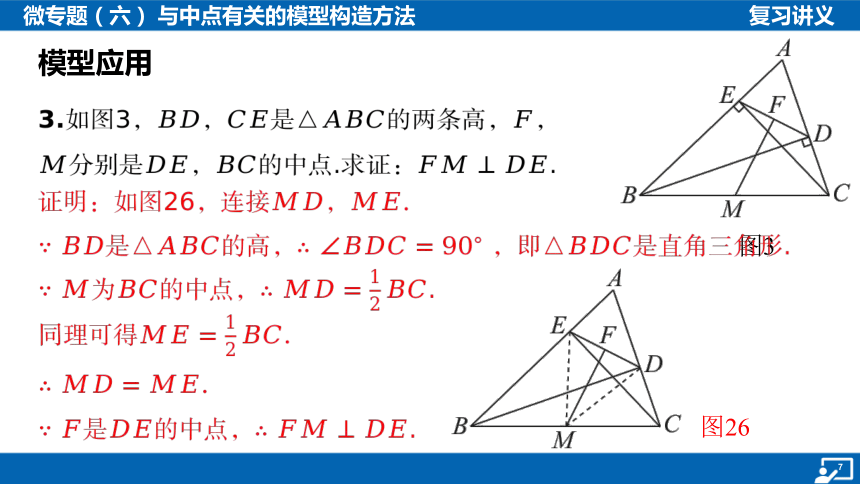
3.如图3,,是的两条高,,分别是, 的中点.求证: .
图3
证明:如图26,连接,
是的高, ,即是直角三角形.
为的中点, .
同理可得
是的中点, .
图26
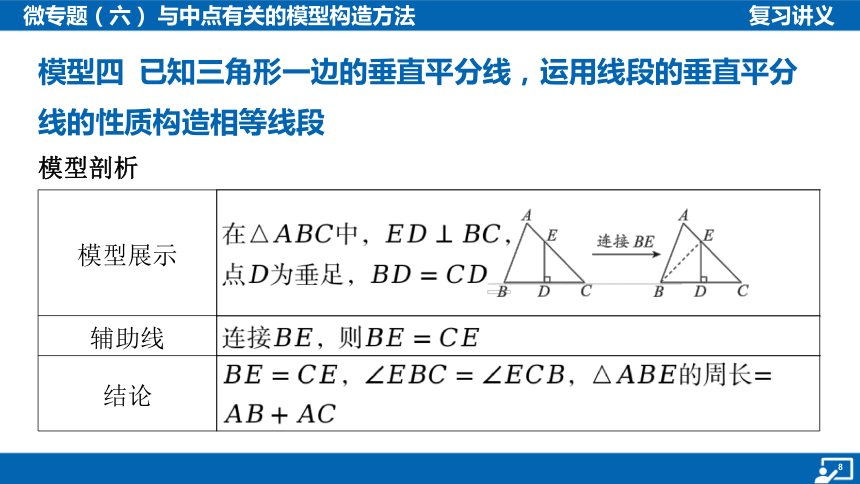
模型四 已知三角形一边的垂直平分线,运用线段的垂直平分
线的性质构造相等线段
模型剖析
模型展示 在中,,
点为垂足, _________________________________________________
辅助线 连接,则
结论 ,,的周长
模型应用
图4
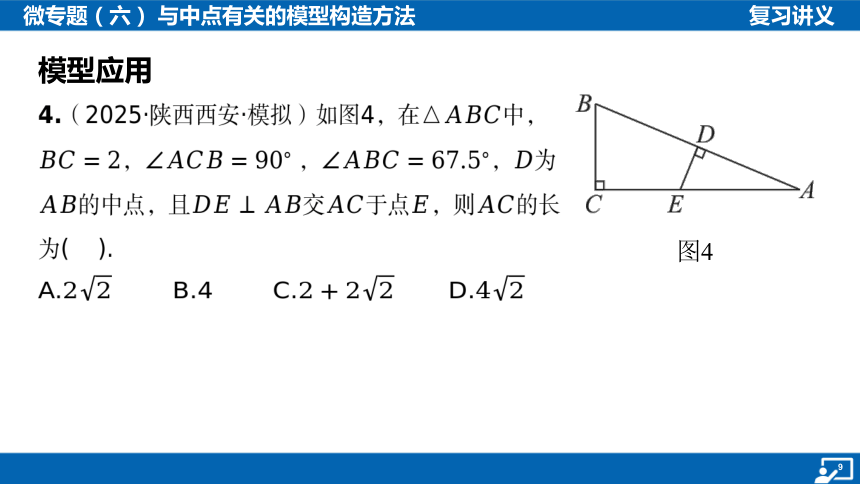
4.(2025·陕西西安·模拟)如图4,在 中,
, ,, 为
的中点,且交于点,则 的长
为( ).
A. B.4 C. D.
提示:连接,由题意可知,垂直平分 ,
所以 .从而得
.由三角形外
角的性质,得 .则
是等腰直角三角形.由此可得,
, .故
.
【答案】C
图4
模型五 已知三角形一边的中线,运用倍长中线构造全等三角形
模型剖析
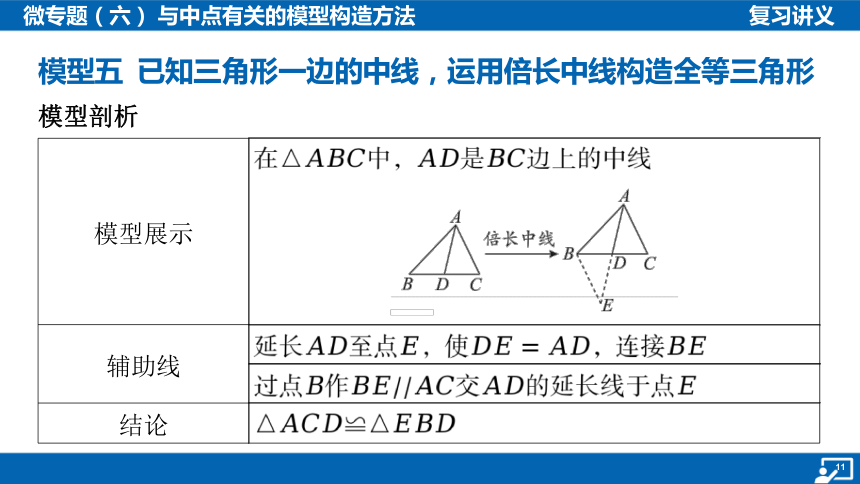
模型展示 在中,是 边上的中线
________________________________________________________________________
辅助线 延长至点,使,连接
过点作交的延长线于点
结论
模型应用
图5
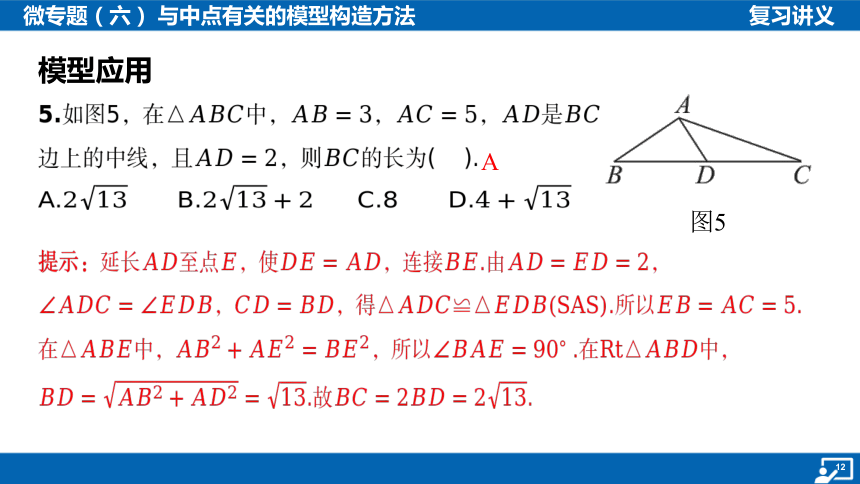
5.如图5,在中,,,是
边上的中线,且,则 的长为( ).
A
A. B. C.8 D.
提示:延长至点,使,连接.由 ,
,,得.所以 .
在中,,所以 .在 中,
.故 .
模型六 已知过中点的线段,利用倍长法构造全等三角形
模型剖析
模型展示 在中,是边的中点,是 上一点,连接
.
__________________________________________________________________________
辅助线 延长至点,使,连接
过点作交的延长线于点
结论
模型应用
6.如图6,在中, ,为的中点,, 交
于点,交于点.请探究线段,, 之间的数量关系,
并说明理由.
解:.
理由:如图27,延长 至点,使,连接,
是 的中点,
.
图27
图27
在和中,,,,
,
, .
,,即垂直平分, .
在 中,, .
微专题练习(六) 与中点有关的模型构造方法
模型一 已知三角形一边的中点,构造中位线
图1
1.如图1,在中,延长至点,使得 ,过
的中点作(点位于点右侧),且 ,
连接.若,则 的长为( ).
A.2 B.3 C.4 D.5
提示:取的中点,连接,则是 的中位线,从而得,.又 ,所以.又,所以四边形 是平行四边形.故 .
C
2.如图2,在四边形中,,,分别是, 的中点,连接并延长,分别与,的延长线交于点, .求证:
.
图2
图30
证明:如图30,连接,取的中点 ,连接
,
,分别是,的中点, ,,,
,
,∴
.
模型二 已知等腰三角形底边的中点,运用“三线合一”的性质
构造垂直
图3
3.如图3,在中,,, 为
的中点,于点,则 的长为( ).
A.2 B. C. D.4
图3
提示:连接.由,,为 的中点,
得, ,
. 在 中,
.又 ,则
,所以
.
【答案】B
4.如图4,在中,,是的中点,, ,且.求证: .
图4
图31
证明:如图31,连接, ,是 的中点, ,即 .
在R和中,,,
,即 .
模型三 已知直角三角形斜边的中点,构造斜边上的中线
5.(2023·湖南郴州·中考)如图5,在中, ,
,,是的中点,则 ___.
5
图5
图6
6.如图6,在 中, , ,
,将直角三角尺的直角顶点与边的中点
重合,直角三角尺绕点 旋转,两条直角边分别交
边于点,,则 的最小值为____.
4.8
提示:因为,,,为 的
中点,所以,.取的中点,连接 ,
则.当时,最小,即最小.由 ,
得. 解得.故 的最小值为4.8.
模型四 已知三角形一边的垂直平分线,运用线段的垂直平分
线的性质构造相等的线段
图7
7.如图7,在中, ,垂直平分 ,
分别交,于,两点.若,,则
的长为( ).
C
A.2 B.3 C.4 D.5
8.如图8,在中, , , 的垂直平分线分
别交,于点,.若,则 ___.
2
图8
模型五 已知三角形一边的中线,运用倍长中线构造全等三角形
9.如图9,在中, ,,为 的中点,
,则 的面积是_____.
图9
图32
提示:由, ,得
.如图32,延长至点 ,使
.因为为的中点,所以 .又
,所以 .所
以, ,
.在中, .故
.
10.如图10,在中,是边上的中线,是上一点,连接 并延长交于点,.求证: .
图10
图33
证明:如图33,延长至点,使 ,连接.
在和中, ,,,
,
,.
又,
.
模型六 已知过中点的线段,利用倍长类中线构造全等三角形
11.如图11,在正方形中,为边的中点,,分别为边 ,
上的点.若,, ,则 的长为___.
图11
图34
提示:如图34,延长交 的延长线于点.由正方形的性质,得 .从而得.因为为的中点,所以 .又,所以 .由此可得,.又,所以 垂直平分.从而得 .故 .
答案:6
12.如图12,在中,,,是锐角, 于点,是的中点,连接,.当 时,求 的长.
图12
图35
解:如图35,延长交的延长线于点 ,连接
,设
四边形是平行四边形,
是的中点, .
在和中, ,,
,
图35
,
,即, 垂直平分
∴ ,, ,即
.
由勾股定理,得,即 .
解得,(不合题意,舍去)
∴ .
复习讲义
第一篇 考点精讲
专题四 三角形
微专题(六) 与中点有关的模型构造方法
模型一 已知三角形一边的中点,构造中位线
模型剖析
模型展示 已知,点是 的中点
_______________________________________________________________________________
辅助线 取的中点,连接
过点作交于点
结论 ,,
模型应用
图1
1.如图1,在中, ,,
是边的中点,点在边上,若 ,
则 ___.
6
提示:取的中点,连接,则为
的中位线,从而得, .所以
.又 ,所以 .
模型二 已知等腰三角形底边的中点,运用“三线合一”的性质
构造垂直
模型剖析
模型展示 为等腰三角形底边 的中点
_____________________________________
辅助线 连接,则 是顶角的平分线、底边上的中线、底边
上的高(三线合一)
结论 ,平分
模型应用
图2
2.如图2,在中,,,点在
上,且,点,分别是, 的中点,
则 的长是( ).
B
A.3 B.4 C.5 D.6
提示:连接,则 .又是 的中点,
,所以 .
模型三 已知直角三角形斜边的中点,构造斜边上的中线
模型剖析
模型展示 在中, ,为 的中点
_____________________________________________________________________
辅助线 连接,则线段是 斜边上的中线
结论
模型应用
3.如图3,,是的两条高,,分别是, 的中点.求证: .
图3
证明:如图26,连接,
是的高, ,即是直角三角形.
为的中点, .
同理可得
是的中点, .
图26
模型四 已知三角形一边的垂直平分线,运用线段的垂直平分
线的性质构造相等线段
模型剖析
模型展示 在中,,
点为垂足, _________________________________________________
辅助线 连接,则
结论 ,,的周长
模型应用
图4
4.(2025·陕西西安·模拟)如图4,在 中,
, ,, 为
的中点,且交于点,则 的长
为( ).
A. B.4 C. D.
提示:连接,由题意可知,垂直平分 ,
所以 .从而得
.由三角形外
角的性质,得 .则
是等腰直角三角形.由此可得,
, .故
.
【答案】C
图4
模型五 已知三角形一边的中线,运用倍长中线构造全等三角形
模型剖析
模型展示 在中,是 边上的中线
________________________________________________________________________
辅助线 延长至点,使,连接
过点作交的延长线于点
结论
模型应用
图5
5.如图5,在中,,,是
边上的中线,且,则 的长为( ).
A
A. B. C.8 D.
提示:延长至点,使,连接.由 ,
,,得.所以 .
在中,,所以 .在 中,
.故 .
模型六 已知过中点的线段,利用倍长法构造全等三角形
模型剖析
模型展示 在中,是边的中点,是 上一点,连接
.
__________________________________________________________________________
辅助线 延长至点,使,连接
过点作交的延长线于点
结论
模型应用
6.如图6,在中, ,为的中点,, 交
于点,交于点.请探究线段,, 之间的数量关系,
并说明理由.
解:.
理由:如图27,延长 至点,使,连接,
是 的中点,
.
图27
图27
在和中,,,,
,
, .
,,即垂直平分, .
在 中,, .
微专题练习(六) 与中点有关的模型构造方法
模型一 已知三角形一边的中点,构造中位线
图1
1.如图1,在中,延长至点,使得 ,过
的中点作(点位于点右侧),且 ,
连接.若,则 的长为( ).
A.2 B.3 C.4 D.5
提示:取的中点,连接,则是 的中位线,从而得,.又 ,所以.又,所以四边形 是平行四边形.故 .
C
2.如图2,在四边形中,,,分别是, 的中点,连接并延长,分别与,的延长线交于点, .求证:
.
图2
图30
证明:如图30,连接,取的中点 ,连接
,
,分别是,的中点, ,,,
,
,∴
.
模型二 已知等腰三角形底边的中点,运用“三线合一”的性质
构造垂直
图3
3.如图3,在中,,, 为
的中点,于点,则 的长为( ).
A.2 B. C. D.4
图3
提示:连接.由,,为 的中点,
得, ,
. 在 中,
.又 ,则
,所以
.
【答案】B
4.如图4,在中,,是的中点,, ,且.求证: .
图4
图31
证明:如图31,连接, ,是 的中点, ,即 .
在R和中,,,
,即 .
模型三 已知直角三角形斜边的中点,构造斜边上的中线
5.(2023·湖南郴州·中考)如图5,在中, ,
,,是的中点,则 ___.
5
图5
图6
6.如图6,在 中, , ,
,将直角三角尺的直角顶点与边的中点
重合,直角三角尺绕点 旋转,两条直角边分别交
边于点,,则 的最小值为____.
4.8
提示:因为,,,为 的
中点,所以,.取的中点,连接 ,
则.当时,最小,即最小.由 ,
得. 解得.故 的最小值为4.8.
模型四 已知三角形一边的垂直平分线,运用线段的垂直平分
线的性质构造相等的线段
图7
7.如图7,在中, ,垂直平分 ,
分别交,于,两点.若,,则
的长为( ).
C
A.2 B.3 C.4 D.5
8.如图8,在中, , , 的垂直平分线分
别交,于点,.若,则 ___.
2
图8
模型五 已知三角形一边的中线,运用倍长中线构造全等三角形
9.如图9,在中, ,,为 的中点,
,则 的面积是_____.
图9
图32
提示:由, ,得
.如图32,延长至点 ,使
.因为为的中点,所以 .又
,所以 .所
以, ,
.在中, .故
.
10.如图10,在中,是边上的中线,是上一点,连接 并延长交于点,.求证: .
图10
图33
证明:如图33,延长至点,使 ,连接.
在和中, ,,,
,
,.
又,
.
模型六 已知过中点的线段,利用倍长类中线构造全等三角形
11.如图11,在正方形中,为边的中点,,分别为边 ,
上的点.若,, ,则 的长为___.
图11
图34
提示:如图34,延长交 的延长线于点.由正方形的性质,得 .从而得.因为为的中点,所以 .又,所以 .由此可得,.又,所以 垂直平分.从而得 .故 .
答案:6
12.如图12,在中,,,是锐角, 于点,是的中点,连接,.当 时,求 的长.
图12
图35
解:如图35,延长交的延长线于点 ,连接
,设
四边形是平行四边形,
是的中点, .
在和中, ,,
,
图35
,
,即, 垂直平分
∴ ,, ,即
.
由勾股定理,得,即 .
解得,(不合题意,舍去)
∴ .
同课章节目录
