2026年中考《数学》复习课件:专题一 数与式-第4讲 分式(35张PPT)
文档属性
| 名称 | 2026年中考《数学》复习课件:专题一 数与式-第4讲 分式(35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 07:22:50 | ||
图片预览










文档简介
(共35张PPT)
复习讲义
第一篇 吃透考点
专题一 数与式
第4讲 分式
聚焦核心
1.分式及其基本性质
定义 若,表示两个______,且 中含有______,则
叫作分式
有意义的条件 当_______时,分式 有意义
值为0的条件 当_______且_______时,分式 的值为0
基本性质 __________________________________________________________________________________________________
整式
字母
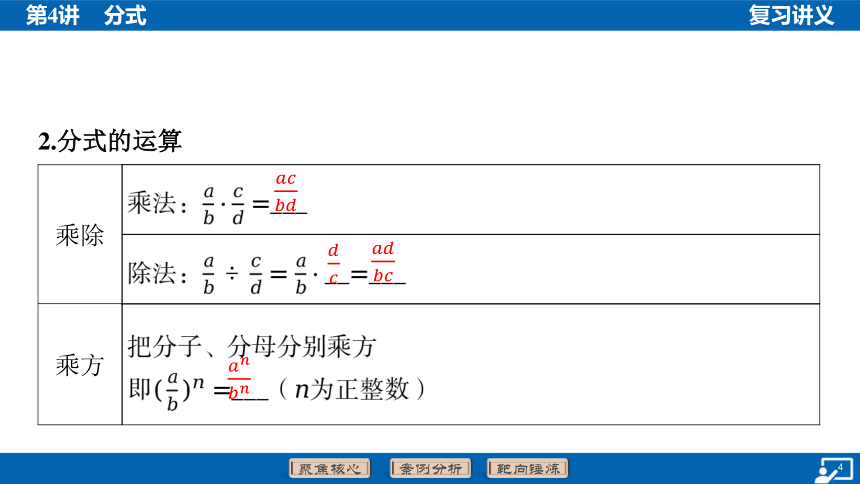
2.分式的运算
乘除 乘法: ___
除法: __ ___
乘方 把分子、分母分别乘方
即___( 为正整数)
加减 同分母分式相加减:分母不变,把分子相______
即 ____
异分母分式相加减:先通分,变为同分母分式,再加减
即___ ______
混合 运算 先算乘方,然后算乘除,进行约分化简后,再算加减.遇到括
号,先算括号里面的.运算结果必须是最简分式或整式
加减
续表
第4讲 分式
案例分析
考点一 分式的有关概念及性质
名师指导
1.分式有意义的条件:分母不为0.
2.分式的值为0的条件:分子等于0且分母不等于0.
3.约分的方法:根据分式的基本性质,当分子、分母都是单项式时,
可直接约去分子、分母系数的最大公因数和分子、分母中相同字母的最
低次幂;当分子、分母中有多项式时,应先将多项式因式分解,再约分.
如
4.确定最简公分母的方法:
(1)分母能因式分解的,先因式分解;
(2)取各分母的系数的最小公倍数;
(3)取各分母中所有字母因式的最高次幂的积.
如分式和的最简公分母是,分式和 的最简公分母
是
例1 一题多问 已知分式 .
(1)若该分式有意义,则 的取值范围是________.
提示:要使分式有意义,则.解得 .
(2)若该分式的值为0,则 的值为___.
1
提示:要使分式的值为0,则,且.解得 .
思路点拨(1)分式有意义 .
思路点拨(2)分式的值为且 .
(3)化简: ______.
提示: .
思路点拨(3)先将分子的多项式因式分解,再约去分子、分母的公因式.
变式 无论 取何值,下列代数式的值不可能为0的是( ).
C
A. B. C. D.
考点专练
1.若分式有意义,则的取值范围是______;若该分式的值为0,则
的值为____.
2.开放性题 (2024·吉林·中考)当分式 的值为正数时,写出一个满
足条件的 的值:________________________________________.
3.分式与 的最简公分母是_______.
1(答案不唯一,取大于的任意数均可)
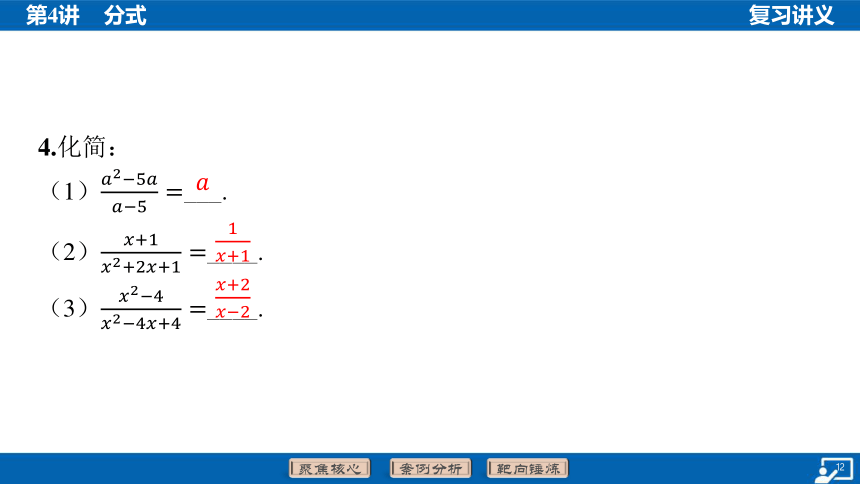
4.化简:
(1) ___.
(2) ____.
(3) ____.
考点二 分式的运算
名师指导
1.进行分式的混合运算时,要先观察整个式子,确定运算顺序,再
一步一步地进行计算.
2.进行异分母分式的加减时,要先通分;当某一项是整式时,可将
该项看作分母为“1”的分式,然后通分.
3.分式运算中,能用运算律的尽量使用运算律,使计算过程更简便.
4.分子、分母中的多项式能因式分解的,应先进行因式分解.
5.分式运算的结果通常要化成最简分式或整式.
例2 (2024·甘肃临夏·中考)
化简: .
思路点拨 先用异分母分式的加减法则计算括号内的,再将除法转化为
乘法进行约分化简.进行括号内的运算时,可把“”看作“ ”,再通分.
解:原式
.
考点专练
5.下列各式计算正确的是( ).
D
A. B.
C. D.
6.计算:
(1)(2025·湖北十堰·中考模拟) ;
解:原式 .
(2) .
解:原式=
=.
考点三 分式的化简求值
名师指导
分式的化简求值需要注意以下三点:(1)明确运算顺序,先算乘
方,再算乘除,最后算加减,有括号先算括号里的;(2)检查化简结
果是否约分到位,是否为最简结果;(3)求值时,若没有明确给出未
知数的值,则所选择代入的值要使各分式有意义,即在化简过程中,分
母、除式都不为0.
例3 (2024·四川广安·中考)先化简,再从 ,
0,1,2中选取一个适合的数代入求值.
思路点拨 先将括号内的项通分后相减,然后将除法转化为乘法,约分
得到化简结果,在计算过程中分子、分母能因式分解的先进行因式分解.
选的数要使原式的所有分母和除式的分子都不为0.
解:原式.
因为且,即且,所以可取0或2.
当时,原式.或当时,原式.
考点专练
7.(2025·湖南衡阳·中考模拟)已知,则代数式 的值为__.
提示:原式.当时,原式 .
8.先化简,再求值:
(1)(2024·湖南·中考)
,其中 .
解:原式.
当时,原式=.
(2)(2024·江苏盐城·中考)
,其中 .
解:原式.
当时,原式.
第4讲 分式
靶向锤炼
靶向练
1.代数式,,,,, 中,属于分式的有( ).
B
A.2个 B.3个 C.4个 D.5个
2.(2025·广西梧州·模拟)若有意义,则 的取值范围是( ).
B
A. B. C. D.
3.若 ,则下列分式化简正确的是( ).
D
A. B. C. D.
4.(2025·广西桂林·模拟)计算 的结果为( ).
C
A. B.1 C. D.
5.下列计算正确的是( ).
C
A. B.
C. D.
6.若分式的值为0,则 的值为___.
0
7.(1)(2024·四川·中考)
化简: ;
解:原式 .
(2)化简: .
解:原式
.
8.(2024·山东·中考)先化简,再求值:,其中 .
解:原式.
当时,原式.
攻坚练
图1
9.(2025·广西玉林·中考模拟)若 是非
负整数,则表示 的值的
对应点落在图1所示的数轴上的范围
是( ).
A.① B.② C.③ D.①或②
提示:原式 .
B
10.(2024·河北·中考)已知为整式,若计算的结果为 ,
则 ( ).
A
A. B. C. D.
提示:由题意,得= .
11.(2024·四川眉山·中考)已知且 ,
,, ,,则 ____.
提示:因为,所以 ,
,.由此可得, ,
,, ,,每三个式子为一个周期.因为 ,
所以 .
12.(2024·黑龙江牡丹江·中考)先化简,再从 ,0,
1,2,3中选一个合适的数代入求值.
解:原式.
因为且,即且,所以可取或1或2.
当时,原式=或当时,原式;
或当时,原式=.
13.(2024·北京·中考)已知,求代数式 的值.
解:由,得.
所以原式=.
拔尖练
14.(2024·内蒙古呼和浩特·中考)[人教版八上第136页例3变式]某研究人员对分别种植在两块试验田中的“丰收1号”和“丰收2号”两种小麦进行研究,两块试验田共产粮 ,种植“丰收1号”小麦的试验田产粮量比种植“丰收2号”小麦的试验田产粮量的1.2倍
少 ,其中“丰收1号”小麦种植在如图2的试
验田中,它是边长为 的正方形去掉一
个边长为 的正方形蓄水池后余下的部分,“丰
收2号”小麦种植在边长为 的正方形试验
田中(如图3).
图2
图3
图2
图3
(1)请分别求出种植“丰收1号”小麦和“丰收2号”小麦两块试验田的产粮量.
解:设种植“丰收2号”小麦的试验田的产粮量为,则种植“丰收1号”小麦的试验田的产粮量为.
根据题意,得.
解得.
则1.
答:种植“丰收1号”小麦和“丰收2号”小麦两块试验田的产粮量都为.
(2)哪种小麦的单位面积产量高?高的单位面积产量是低的单位面积
产量的多少倍?
图2
图3
解:根据题意,得“丰收1号”小麦的单位面积产量为,“丰收2号”小麦的单位面积产量为.
因为,所以.
所以“丰收2号”小麦的单位面积产量高.
所以,故“丰收2号”小麦的单位面积产量是“丰收1号”小麦的单位面积产量的倍.
图2
图3
复习讲义
第一篇 吃透考点
专题一 数与式
第4讲 分式
聚焦核心
1.分式及其基本性质
定义 若,表示两个______,且 中含有______,则
叫作分式
有意义的条件 当_______时,分式 有意义
值为0的条件 当_______且_______时,分式 的值为0
基本性质 __________________________________________________________________________________________________
整式
字母
2.分式的运算
乘除 乘法: ___
除法: __ ___
乘方 把分子、分母分别乘方
即___( 为正整数)
加减 同分母分式相加减:分母不变,把分子相______
即 ____
异分母分式相加减:先通分,变为同分母分式,再加减
即___ ______
混合 运算 先算乘方,然后算乘除,进行约分化简后,再算加减.遇到括
号,先算括号里面的.运算结果必须是最简分式或整式
加减
续表
第4讲 分式
案例分析
考点一 分式的有关概念及性质
名师指导
1.分式有意义的条件:分母不为0.
2.分式的值为0的条件:分子等于0且分母不等于0.
3.约分的方法:根据分式的基本性质,当分子、分母都是单项式时,
可直接约去分子、分母系数的最大公因数和分子、分母中相同字母的最
低次幂;当分子、分母中有多项式时,应先将多项式因式分解,再约分.
如
4.确定最简公分母的方法:
(1)分母能因式分解的,先因式分解;
(2)取各分母的系数的最小公倍数;
(3)取各分母中所有字母因式的最高次幂的积.
如分式和的最简公分母是,分式和 的最简公分母
是
例1 一题多问 已知分式 .
(1)若该分式有意义,则 的取值范围是________.
提示:要使分式有意义,则.解得 .
(2)若该分式的值为0,则 的值为___.
1
提示:要使分式的值为0,则,且.解得 .
思路点拨(1)分式有意义 .
思路点拨(2)分式的值为且 .
(3)化简: ______.
提示: .
思路点拨(3)先将分子的多项式因式分解,再约去分子、分母的公因式.
变式 无论 取何值,下列代数式的值不可能为0的是( ).
C
A. B. C. D.
考点专练
1.若分式有意义,则的取值范围是______;若该分式的值为0,则
的值为____.
2.开放性题 (2024·吉林·中考)当分式 的值为正数时,写出一个满
足条件的 的值:________________________________________.
3.分式与 的最简公分母是_______.
1(答案不唯一,取大于的任意数均可)
4.化简:
(1) ___.
(2) ____.
(3) ____.
考点二 分式的运算
名师指导
1.进行分式的混合运算时,要先观察整个式子,确定运算顺序,再
一步一步地进行计算.
2.进行异分母分式的加减时,要先通分;当某一项是整式时,可将
该项看作分母为“1”的分式,然后通分.
3.分式运算中,能用运算律的尽量使用运算律,使计算过程更简便.
4.分子、分母中的多项式能因式分解的,应先进行因式分解.
5.分式运算的结果通常要化成最简分式或整式.
例2 (2024·甘肃临夏·中考)
化简: .
思路点拨 先用异分母分式的加减法则计算括号内的,再将除法转化为
乘法进行约分化简.进行括号内的运算时,可把“”看作“ ”,再通分.
解:原式
.
考点专练
5.下列各式计算正确的是( ).
D
A. B.
C. D.
6.计算:
(1)(2025·湖北十堰·中考模拟) ;
解:原式 .
(2) .
解:原式=
=.
考点三 分式的化简求值
名师指导
分式的化简求值需要注意以下三点:(1)明确运算顺序,先算乘
方,再算乘除,最后算加减,有括号先算括号里的;(2)检查化简结
果是否约分到位,是否为最简结果;(3)求值时,若没有明确给出未
知数的值,则所选择代入的值要使各分式有意义,即在化简过程中,分
母、除式都不为0.
例3 (2024·四川广安·中考)先化简,再从 ,
0,1,2中选取一个适合的数代入求值.
思路点拨 先将括号内的项通分后相减,然后将除法转化为乘法,约分
得到化简结果,在计算过程中分子、分母能因式分解的先进行因式分解.
选的数要使原式的所有分母和除式的分子都不为0.
解:原式.
因为且,即且,所以可取0或2.
当时,原式.或当时,原式.
考点专练
7.(2025·湖南衡阳·中考模拟)已知,则代数式 的值为__.
提示:原式.当时,原式 .
8.先化简,再求值:
(1)(2024·湖南·中考)
,其中 .
解:原式.
当时,原式=.
(2)(2024·江苏盐城·中考)
,其中 .
解:原式.
当时,原式.
第4讲 分式
靶向锤炼
靶向练
1.代数式,,,,, 中,属于分式的有( ).
B
A.2个 B.3个 C.4个 D.5个
2.(2025·广西梧州·模拟)若有意义,则 的取值范围是( ).
B
A. B. C. D.
3.若 ,则下列分式化简正确的是( ).
D
A. B. C. D.
4.(2025·广西桂林·模拟)计算 的结果为( ).
C
A. B.1 C. D.
5.下列计算正确的是( ).
C
A. B.
C. D.
6.若分式的值为0,则 的值为___.
0
7.(1)(2024·四川·中考)
化简: ;
解:原式 .
(2)化简: .
解:原式
.
8.(2024·山东·中考)先化简,再求值:,其中 .
解:原式.
当时,原式.
攻坚练
图1
9.(2025·广西玉林·中考模拟)若 是非
负整数,则表示 的值的
对应点落在图1所示的数轴上的范围
是( ).
A.① B.② C.③ D.①或②
提示:原式 .
B
10.(2024·河北·中考)已知为整式,若计算的结果为 ,
则 ( ).
A
A. B. C. D.
提示:由题意,得= .
11.(2024·四川眉山·中考)已知且 ,
,, ,,则 ____.
提示:因为,所以 ,
,.由此可得, ,
,, ,,每三个式子为一个周期.因为 ,
所以 .
12.(2024·黑龙江牡丹江·中考)先化简,再从 ,0,
1,2,3中选一个合适的数代入求值.
解:原式.
因为且,即且,所以可取或1或2.
当时,原式=或当时,原式;
或当时,原式=.
13.(2024·北京·中考)已知,求代数式 的值.
解:由,得.
所以原式=.
拔尖练
14.(2024·内蒙古呼和浩特·中考)[人教版八上第136页例3变式]某研究人员对分别种植在两块试验田中的“丰收1号”和“丰收2号”两种小麦进行研究,两块试验田共产粮 ,种植“丰收1号”小麦的试验田产粮量比种植“丰收2号”小麦的试验田产粮量的1.2倍
少 ,其中“丰收1号”小麦种植在如图2的试
验田中,它是边长为 的正方形去掉一
个边长为 的正方形蓄水池后余下的部分,“丰
收2号”小麦种植在边长为 的正方形试验
田中(如图3).
图2
图3
图2
图3
(1)请分别求出种植“丰收1号”小麦和“丰收2号”小麦两块试验田的产粮量.
解:设种植“丰收2号”小麦的试验田的产粮量为,则种植“丰收1号”小麦的试验田的产粮量为.
根据题意,得.
解得.
则1.
答:种植“丰收1号”小麦和“丰收2号”小麦两块试验田的产粮量都为.
(2)哪种小麦的单位面积产量高?高的单位面积产量是低的单位面积
产量的多少倍?
图2
图3
解:根据题意,得“丰收1号”小麦的单位面积产量为,“丰收2号”小麦的单位面积产量为.
因为,所以.
所以“丰收2号”小麦的单位面积产量高.
所以,故“丰收2号”小麦的单位面积产量是“丰收1号”小麦的单位面积产量的倍.
图2
图3
同课章节目录
