2026年中考《数学》复习课件：专题一 数与式-第5讲 二次根式（33张PPT）

(共33张PPT)
复习讲义
第一篇 吃透考点
专题一 数与式
第5讲 二次根式
聚焦核心
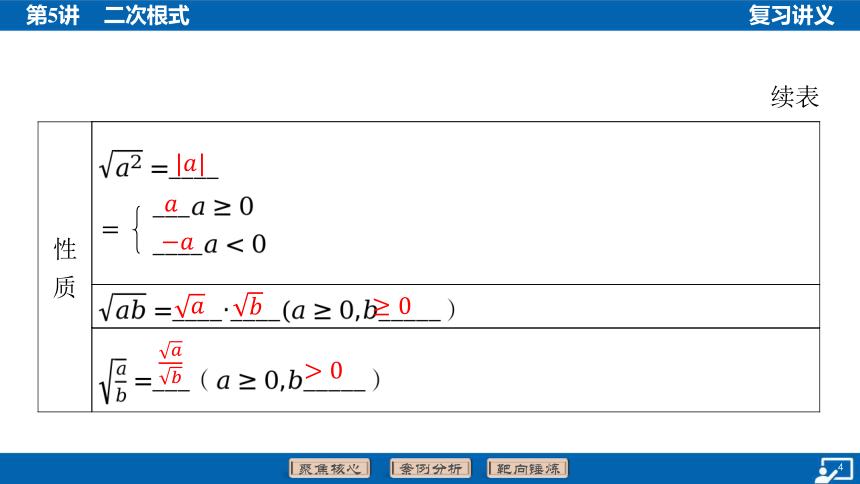
1.二次根式的概念及其性质
相 关 概 念 定义：形如 ___0）的式子叫作二次根式
最简二次根式：必须同时满足以下两个条件
（1）被开方数不含______
（2）被开方数中不含能__________的因数或因式
性 质 非负性：当时， ___0
___
分母
开得尽方
性 质 ____
___
____
____·____, _____）
___（, _____）
续表
=
2.二次根式的运算
乘除运 算 乘法 _____
除法 _ ___
加减运 算 先将二次根式化成______________，再将__________相同的 二次根式合并
最简二次根式
被开方数
第5讲 二次根式
案例分析
考点一 二次根式的相关概念
名师指导
1.二次根式在实数范围内有意义的条件是被开方数为非负数.在分式
中，还要使分母不为0.
2.化二次根式为最简二次根式的方法:（1）若被开方数是分数
（包括小数）或分式，则先利用二次根式的性质把它写成二次根式除法
的形式，然后把分母化为有理数或有理式;（2）若被开方数是整数或整式，
则先将它分解因数或因式，然后把开得尽方的因数或因式开方后移出根
号外.
例1 教材变式［湘教版八上第174页第1题变式］当 是怎样的实数时，
下列二次根式有意义？
（1） ；
解：由，得.因此当时, 在实数范围内有意义.
（2） ；
解：因为,所以为全体实数时,在实数范围内有意义.
思路点拨 二次根式 在实数范围内有意义的条件：被开方数为非负实
数，即 .
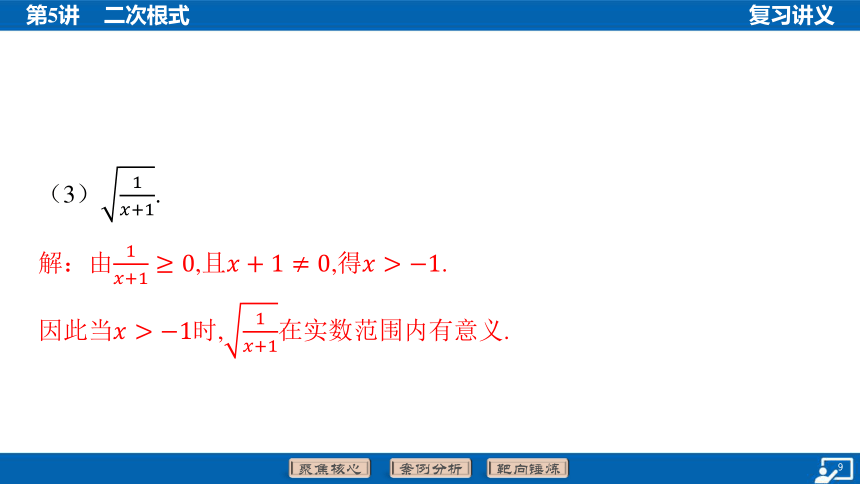
（3） .
解：由,且,得.
因此当时,在实数范围内有意义.
考点专练
1.（2025·广西南宁·模拟）下列式子为最简二次根式的是( ).
B
A. B. C. D.
2.（2025·广西河池·模拟）要使式子在实数范围内有意义， 应满
足的条件是______.
3.（2024·广西北部湾经济区·中考）化简： _____.
考点二 二次根式的性质
名师指导
1.二次根式的双重非负性：
（1）被开方数是非负数，即；
（2） 是非负数，即.
2.如果几个非负数的和等于0，那么这几个数都等于0.
3.，（为任意实数）.
例2 （2024·四川乐山·中考）已知，化简
的结果为( ).
A. B.1 C. D.
提示：由二次根式的性质，得.因为 ，所以
, .所以 .
思路点拨 先根据化简二次根式，再根据 去绝对值符号.
B
考点专练
4.（2024·内蒙古呼伦贝尔·中考）实数, 在数轴上的对应位置如图1所
示，则 的化简结果是( ).
图1
A.2 B. C. D.
提示：由题图可知， ，0 .所以.因此 .
A
5.（2023·江苏连云港·中考）计算： ___.
6.（2025·柳州·中考模拟）若实数， 满足
，则 ___.
5
7
提示：因为，又 ，
，所以， .解方程组
得所以 .
考点三 二次根式的运算
名师指导
1.二次根式的乘除：根号外含有因数的，先将这些因数相乘（除）
作为结果的因数，再将根号内的被开方数相乘（除）.
2.二次根式的加减：先将二次根式化为最简二次根式，再将被开方
数相同的二次根式合并.
3.二次根式的混合运算：先将二次根式化为最简二次根式，再运算.
能运用乘法公式的，运用乘法公式简便运算.运算顺序是先乘方，再乘
除，最后加减，有括号先算括号里面的.
例3 （2024·山东济宁·中考）下列各式运算正确的是( ).
A. B.
C. D.
提示：与不能合并，所以选项A错误； ，所以选项B正确； ，所以选项C错误； ，所以选项D错误.
思路点拨 根据二次根式的运算法则，进行逐项判断.
B
考点专练
7.（2025·辽宁大连·中考模拟）下列各式计算正确的是( ).
D
A. B.
C. D.
8.教材变式［湘教版八上第175页第7题变式］我国南宋著名数学家秦九
韶提出了利用三角形三边长，， 求三角形面积的公式，即
.在中，， ，
，则边 上的高为( ).
A. B. C. D.
提示：根据题意，得.所以边 上的高为 .
A
9.（2024·吉林长春·中考）计算： ____.
10.计算： ___________.
11.计算：
（1）（2024·河南·中考） ；
解：原式 .
（2） .
解：原式.
考点四 二次根式的估值及大小比较
名师指导
1.确定与二次根式相邻的两个连续整数的方法：
方法步骤 示例
（1）对二次根式进行平方（2）找出与平方后所得的数相 邻的两个开得尽方的整数（3）对这两个整数开方（4）二 次根式的值在这两个整数的算术平方根之间 ____________________________
2.二次根式比较大小的两种常用方法：
（1）平方法：将要比较大小的两个数先平方，根据平方后数的大
小来确定原数的大小.
（2）作差法：将要比较大小的两个数相减，根据所得的差与0的大
小关系来确定两数的大小.
例4（1）（2024·天津·中考）估算 的值介于( ).
C
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
提示：因为，，所以 ，即
.所以 介于3和4之间.
思路点拨（1）找到两个与的值最接近的开得尽方的整数，的值介于这两个整数的算术平方根之间.
（2）（2024·山东临沂·中考模拟）比较大小：___.（填“ ”“ ”或“ ”）
提示：（方法一）因为，，而 ，所以 .
（方法二）.因为，所以 .则.因此，即.所以 .
<
思路点拨（2）思路一，利用平方法，比较与的大小，得出与 的大小关系；思路二，利用作差法，若，则 ；若 ，则；若，则 .
考点专练
12.（2023·内蒙古赤峰·中考）如图2，数轴上表示实数 的点可能是
( ).
图2
B
A.点 B.点 C.点 D.点
13.（2024·广西桂林·模拟） 是黄金分割数，它体现了数学之美，被
大量用于美术、建筑等领域.估算 的值介于( ).
C
A. 和0之间 B.0和0.5之间 C.0.5和1之间 D.1和1.5之间
14.（2024·山西·中考）比较大小：2.（填“ ”“ ”或“ ”）
第5讲 二次根式
靶向锤炼
达标练
1.（2024·广西玉林·模拟）如果式子有意义，那么 的值可以是
( ).
D
A. B. C. D.1
2.下列二次根式为最简二次根式的是( ).
C
A. B. C. D.
3.下列各式计算正确的是( ).
D
A. B.
C. D.
4.（2024·四川德阳·中考）化简： ___.
5.比较大小：___.（填“ ”“ ”或“ ”）
3
提示：因为，，，所以 .
6.若，则 ___.
7.（2023·天津·中考）计算 的结果为___．
1
1
8.（2023·甘肃兰州·中考）计算： .
解：原式 .
提分练
9.（2024·重庆·中考）已知，则实数 的范围是( ).
B
A. B. C. D.
提示：.因为 ，
所以.所以 .
10.开放性题（2023·湖北黄冈·中考）请写出一个正整数的值,使得
是整数： _________________．
2（答案不唯一）
11.开放性题（2023·山东潍坊·中考）从，， 中任意选择两个
数，分别填在算式里面的“”与“ ”中，该算式的结果
是_ _______________________.
（答案不唯一）
12.（2023·甘肃武威·中考）计算： ．
解：原式 ．
冲刺练
13.理解与运用
【解题示例】已知，求
的值，
解：因为
, ,
所以 .
【方法运用】已知 ，请仿照以上方法求
的值.
解：因为，,所以
.