吉林省长春市2025届中考数学真题(含答案)
文档属性
| 名称 | 吉林省长春市2025届中考数学真题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 10:12:26 | ||
图片预览


文档简介
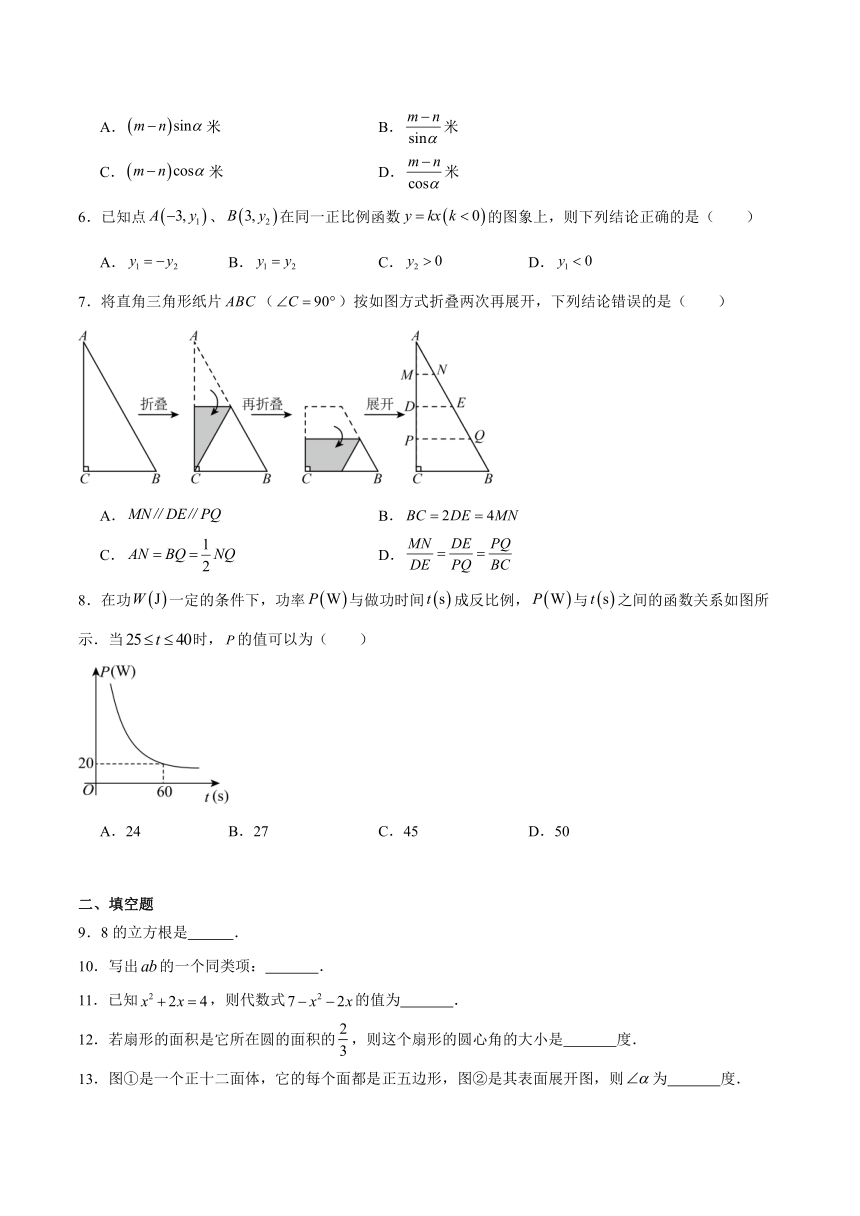
吉林省长春市2025届中考数学试卷
一、单选题
1.中国是最早使用正、负数表示具有相反意义的量的国家.如果水位下降记作,那么水位上升记作( )
A. B. C. D.
2.下面几何体中为圆锥的是( )
A. B.
C. D.
3.下列计算一定正确的是( )
A. B.
C. D.
4.下列不等式组无解的是( )
A. B. C. D.
5.如图,已知某山峰的海拔高度为米,一位登山者到达海拔高度为米的点处.测得山峰顶端的仰角为.则、两点之间的距离为( )
A.米 B.米
C.米 D.米
6.已知点、在同一正比例函数的图象上,则下列结论正确的是( )
A. B. C. D.
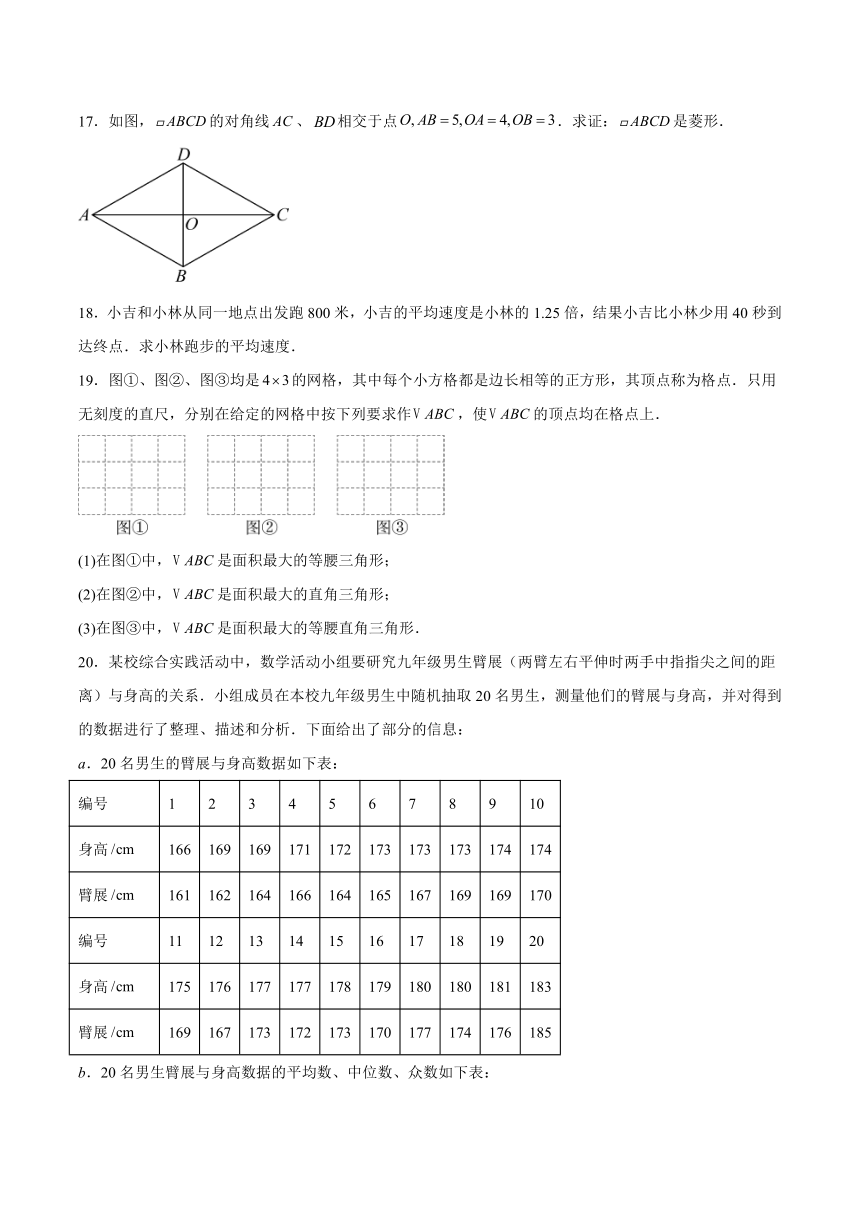
7.将直角三角形纸片()按如图方式折叠两次再展开,下列结论错误的是( )
A. B.
C. D.
8.在功一定的条件下,功率与做功时间成反比例,与之间的函数关系如图所示.当时,的值可以为( )
A.24 B.27 C.45 D.50
二、填空题
9.8的立方根是 .
10.写出的一个同类项: .
11.已知,则代数式的值为 .
12.若扇形的面积是它所在圆的面积的,则这个扇形的圆心角的大小是 度.
13.图①是一个正十二面体,它的每个面都是正五边形,图②是其表面展开图,则为 度.
14.如图,在边长为4的正方形中,对角线、相交于点.点在线段上.连接,作于点,交于点.给出下面四个结论:
①;
②;
③当时,;
④点与点之间的距离的最小值为.
上述结论中,正确结论的序号有 .
三、解答题
15.先化简.再求值:,其中.
16.长春市人民广场是中心景观类环岛型交通广场,以开阔的空间、精美的建筑和多彩的绿化而驰名.甲、乙两辆车从人民大街由南向北驶入人民广场,它们各自从A、B、C三个出口中随机选择一个出口驶出.用画树状图(或列表)的方法,求甲、乙两辆车从同一出口驶出的概率.
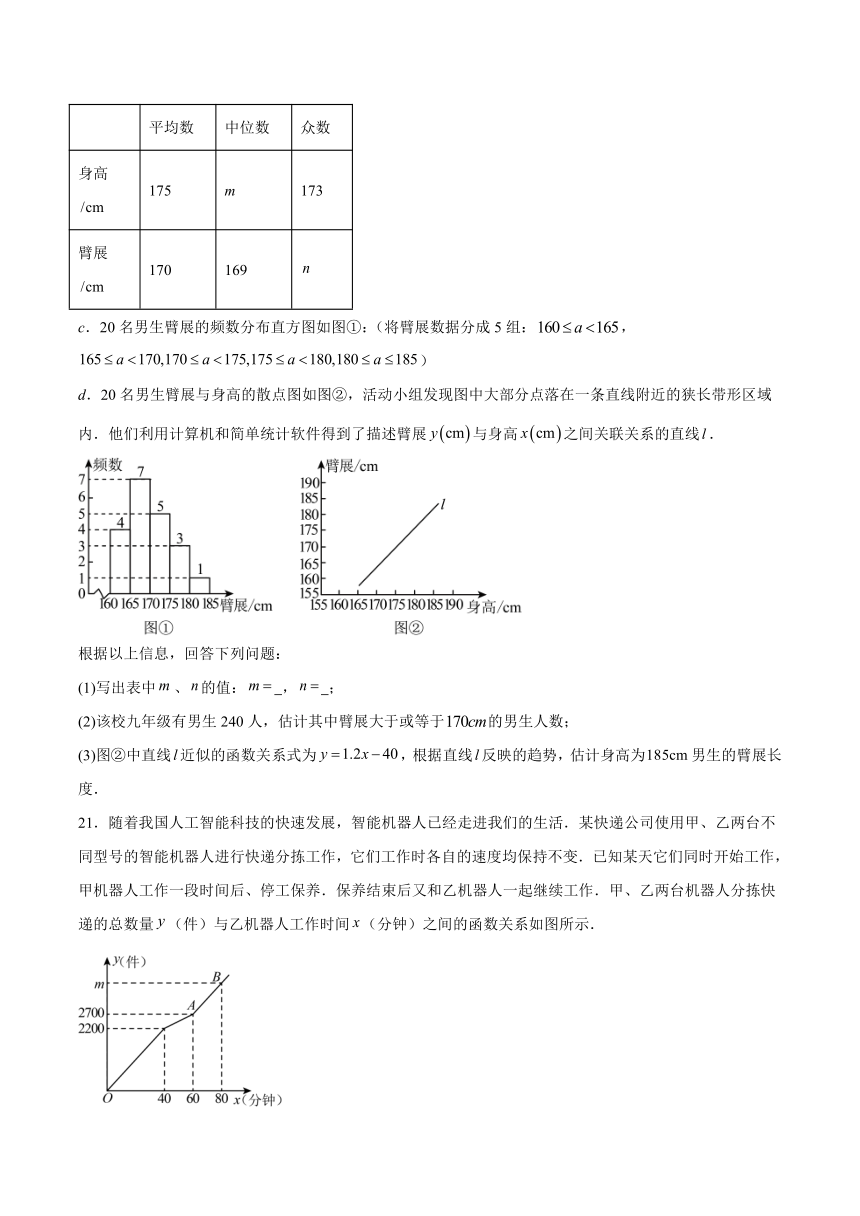
17.如图,的对角线、相交于点.求证:是菱形.
18.小吉和小林从同一地点出发跑800米,小吉的平均速度是小林的1.25倍,结果小吉比小林少用40秒到达终点.求小林跑步的平均速度.
19.图①、图②、图③均是的网格,其中每个小方格都是边长相等的正方形,其顶点称为格点.只用无刻度的直尺,分别在给定的网格中按下列要求作,使的顶点均在格点上.
(1)在图①中,是面积最大的等腰三角形;
(2)在图②中,是面积最大的直角三角形;
(3)在图③中,是面积最大的等腰直角三角形.
20.某校综合实践活动中,数学活动小组要研究九年级男生臂展(两臂左右平伸时两手中指指尖之间的距离)与身高的关系.小组成员在本校九年级男生中随机抽取20名男生,测量他们的臂展与身高,并对得到的数据进行了整理、描述和分析.下面给出了部分的信息:
a.20名男生的臂展与身高数据如下表:
编号 1 2 3 4 5 6 7 8 9 10
身高 166 169 169 171 172 173 173 173 174 174
臂展 161 162 164 166 164 165 167 169 169 170
编号 11 12 13 14 15 16 17 18 19 20
身高 175 176 177 177 178 179 180 180 181 183
臂展 169 167 173 172 173 170 177 174 176 185
b.20名男生臂展与身高数据的平均数、中位数、众数如下表:
平均数 中位数 众数
身高 175 m 173
臂展 170 169
c.20名男生臂展的频数分布直方图如图①:(将臂展数据分成5组:,)
d.20名男生臂展与身高的散点图如图②,活动小组发现图中大部分点落在一条直线附近的狭长带形区域内.他们利用计算机和简单统计软件得到了描述臂展与身高之间关联关系的直线.
根据以上信息,回答下列问题:
(1)写出表中、的值: , ;
(2)该校九年级有男生240人,估计其中臂展大于或等于的男生人数;
(3)图②中直线近似的函数关系式为,根据直线反映的趋势,估计身高为男生的臂展长度.
21.随着我国人工智能科技的快速发展,智能机器人已经走进我们的生活.某快递公司使用甲、乙两台不同型号的智能机器人进行快递分拣工作,它们工作时各自的速度均保持不变.已知某天它们同时开始工作,甲机器人工作一段时间后、停工保养.保养结束后又和乙机器人一起继续工作.甲、乙两台机器人分拣快递的总数量(件)与乙机器人工作时间(分钟)之间的函数关系如图所示.
(1)甲机器人停工保养的时间为 分钟, ;
(2)求所在直线对应的函数表达式;
(3)若该快递公司当天分拣快递的总数批为5450件,则乙机器人工作时间为 分钟.
22.数学活动:探究平面图形的最小覆盖圆
【定义】我们称能完全覆盖某平面图形的圆(即该平面图形上所有的点均在圆内或圆上)为该平面图形的覆盖圆.其中,能完全覆盖平面图形的最小的圆(即直径最小)称为该平面图形的最小覆盖圆.
【探究一】线段的最小覆盖圆
线段的覆盖圆有无数个,其中,以为直径的圆是其最小覆盖圆.
理由如下:易知线段的最小覆盖圆一定经过点、点.如图①,以为直径作,再过、两点作(与不重合),连结.在中,有().
,
,即的直径大于的直径.
是线段的最小覆盖圆.“”处应填写的推理依据为 .
【探究二】直角三角形的最小覆盖圆
要确定直角三角形的最小覆盖圆,我们可先将其转化为【探究一】中线段的最小覆盖圆问题.这样就可以先确定直角三角形最长边(斜边)的最小覆盖圆,再判断直角顶点与这个圆的位置关系,从而确定直角三角形的最小覆盖圆.如图②,在中,.是以为直径的圆.请你判断点与的位置关系,并说明理由.
又由【探究一】可知,是最长边的最小覆盖圆,所以,是的最小覆盖圆.
【拓展应用】矩形的最小覆盖圆
如图③,在矩形中,,.
(1)用圆规和无刻度的直尺在图③中作矩形的最小覆盖圆:(不写做法,保留作图痕迹,作图确定后必须用黑色字迹的签字笔描点)
(2)该矩形的最小覆盖圆的直径为 ;
(3)若用两个等圆完全覆盖矩形.则这样的两个等圆的最小直径为 .
23.如图,在中,,,点为边的中点,点为边上一动点,连接.将线段绕点顺时针旋转得到线段.
(1)线段的长为 ;
(2)当时,求的长;
(3)当点在边上时,求证:;
(4)当点到的距离是点到距离的2倍时,直接写出的长.
24.在平面直角坐标系中,点为坐标原点,抛物线经过点.点、是该抛物线上的两点,横坐标分别为、,已知点,作点关于点的对称点,作点关于点的对称点,构造四边形.
(1)求该抛物线所对应的函数表达式;
(2)当两点关于该抛物线的对称轴对称时,求点的坐标;
(3)设抛物线在、两点之间的部分(含、两点)为图象.当时,若图象的最高点与最低点的纵坐标之差为.求的值;
(4)连结、,当时,直接写出的取值范围(这里、、均是大于且小于的角).
参考答案
题号 1 2 3 4 5 6 7 8
答案 B C A B B A D C
9.2
10.(答案不唯一)
11.3
12.
13.
14.①②④
15.,4
16.
17.见解析
证明:∵,
∴,,
∴,
∴,
∴,
∵四边形是平行四边形,
∴四边形是菱形.
18.小林跑步的平均速度为4米每秒
解:设小林跑步的平均速度为米每秒,则小吉的平均速度为米每秒,
由题意得:,
解得:,
经检验,是原方程的解,且符合题意,
∴原方程的解为:,
答:小林跑步的平均速度为4米每秒.
19.(1)见解析
(2)见解析
(3)见解析
(1)解:如图所示,即为所求;
(2)解;如图所示,即为所求;
(3)解:如图所示,即为所求.
20.(1);
(2)人
(3)身高为男生的臂展长度约为.
(1)解:由表格信息可得:;
;
(2)解:该校九年级有男生240人,估计臂展大于或等于170cm的男生人数为:
(人);
(3)解:∵,
当时,,
∴身高为男生的臂展长度约为.
21.(1),
(2)
(3)该快递公司当天分拣快递的总数批为5450件,则乙机器人工作时间为分钟.
(1)解:由图象可得:甲机器人停工保养的时间为分钟;
∵,
∴(件);
(2)解:∵甲乙机器人的效率为每分钟件,
∴所在直线对应的函数表达式为:;
(3)解:当时,
∴,
解得:,
∴该快递公司当天分拣快递的总数批为5450件,则乙机器人工作时间为分钟.
22.探究一:三角形的任意两边之和大于第三边;探究二:在上;证明见解析;拓展应用:(1)作图见解析;(2);(3);
解:探究一:
理由如下:易知线段的最小覆盖圆一定经过点、点.如图①,以为直径作,再过、两点作(与不重合),连结.在中,有(三角形的任意两边之和大于第三边).
,
,即的直径大于的直径.
是线段的最小覆盖圆.“”处应填写的推理依据为三角形的任意两边之和大于第三边.
故答案为:三角形的任意两边之和大于第三边;
探究二:∵,为的中点,
∴,
∴在上;
拓展应用:(1)如图,即为矩形的最小覆盖圆;
(2)∵矩形,,,
∴,;
(3)作的垂直平分线,交于,交于,
∴四边形,是两个全等的矩形,
∴,
∵用两个等圆完全覆盖矩形,
∴两圆一定过,
连接,交点分别为,
同理可得:这样的两个等圆的最小直径为或或或,
∴最小直径为,
如图,作的垂直平分线交于,
同法作,,此时不是直径最小的等圆;
综上:用两个等圆完全覆盖矩形.则这样的两个等圆的最小直径为.
23.(1)
(2)
(3)证明见解析
(4)的长为或.
(1)解:∵在中,,,
∴;
(2)解:如图,在中,,,点为边的中点,
∴,,
∵,
∴,而,
∴,
∴;
(3)证明:∵旋转,
∴,
如图,∵,,
∴,
∵,,
∴;
(4)解:如图,当在的左边时,结合题意可得:,,,
过作于,过作于,
∴四边形为矩形,
∴,
结合(1)可得:,
∵,,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴;
如图,当在的右边时,过作于,过作于,
同理:,
四边形四边形为矩形,
∴,
∵,
∴,
∴,,
同理可得:,,
∴;
综上:的长为或.
24.(1)
(2)
(3)或
(4)
(1)将点代入中得:
解得:,
∴.
(2)根据抛物线对称轴公式可知:
抛物线的对称轴为,
∵、关于对称轴对称,且横坐标分别为、,
∴、中点在对称轴上,
∴,
,
解得:,
∵点是该抛物线上的点,
将代入抛物线解析式得,
,
即
设是A关于的对称点,则:
解得,,
∴点坐标为.
(3)∵抛物线顶点为,开口向上,,,
当时,包含,最低点为。
当时,,最高点为A,纵坐标差为:,
解得:;
当时,,最高点为B,纵坐标差为: ,
解得:.
综上,m的值为或.
(4)∵点是点关于点的对称点,点是点关于点的对称点,结合题意可知:
∴,,,,
∴,,,,
当、运动到平行四边形内部时(即、、共线),如图:
过点作,如图:
此时,满足,
由一次函数的性质可的大小决定了直线的倾斜方向和函数的增减性,
所以当两条一次函数的直线平行时的大小相同,
∴
∴
解得
当、、共线时,如图,同理:
∴,
∴,
∴,
解得.
综上,.
一、单选题
1.中国是最早使用正、负数表示具有相反意义的量的国家.如果水位下降记作,那么水位上升记作( )
A. B. C. D.
2.下面几何体中为圆锥的是( )
A. B.
C. D.
3.下列计算一定正确的是( )
A. B.
C. D.
4.下列不等式组无解的是( )
A. B. C. D.
5.如图,已知某山峰的海拔高度为米,一位登山者到达海拔高度为米的点处.测得山峰顶端的仰角为.则、两点之间的距离为( )
A.米 B.米
C.米 D.米
6.已知点、在同一正比例函数的图象上,则下列结论正确的是( )
A. B. C. D.
7.将直角三角形纸片()按如图方式折叠两次再展开,下列结论错误的是( )
A. B.
C. D.
8.在功一定的条件下,功率与做功时间成反比例,与之间的函数关系如图所示.当时,的值可以为( )
A.24 B.27 C.45 D.50
二、填空题
9.8的立方根是 .
10.写出的一个同类项: .
11.已知,则代数式的值为 .
12.若扇形的面积是它所在圆的面积的,则这个扇形的圆心角的大小是 度.
13.图①是一个正十二面体,它的每个面都是正五边形,图②是其表面展开图,则为 度.
14.如图,在边长为4的正方形中,对角线、相交于点.点在线段上.连接,作于点,交于点.给出下面四个结论:
①;
②;
③当时,;
④点与点之间的距离的最小值为.
上述结论中,正确结论的序号有 .
三、解答题
15.先化简.再求值:,其中.
16.长春市人民广场是中心景观类环岛型交通广场,以开阔的空间、精美的建筑和多彩的绿化而驰名.甲、乙两辆车从人民大街由南向北驶入人民广场,它们各自从A、B、C三个出口中随机选择一个出口驶出.用画树状图(或列表)的方法,求甲、乙两辆车从同一出口驶出的概率.
17.如图,的对角线、相交于点.求证:是菱形.
18.小吉和小林从同一地点出发跑800米,小吉的平均速度是小林的1.25倍,结果小吉比小林少用40秒到达终点.求小林跑步的平均速度.
19.图①、图②、图③均是的网格,其中每个小方格都是边长相等的正方形,其顶点称为格点.只用无刻度的直尺,分别在给定的网格中按下列要求作,使的顶点均在格点上.
(1)在图①中,是面积最大的等腰三角形;
(2)在图②中,是面积最大的直角三角形;
(3)在图③中,是面积最大的等腰直角三角形.
20.某校综合实践活动中,数学活动小组要研究九年级男生臂展(两臂左右平伸时两手中指指尖之间的距离)与身高的关系.小组成员在本校九年级男生中随机抽取20名男生,测量他们的臂展与身高,并对得到的数据进行了整理、描述和分析.下面给出了部分的信息:
a.20名男生的臂展与身高数据如下表:
编号 1 2 3 4 5 6 7 8 9 10
身高 166 169 169 171 172 173 173 173 174 174
臂展 161 162 164 166 164 165 167 169 169 170
编号 11 12 13 14 15 16 17 18 19 20
身高 175 176 177 177 178 179 180 180 181 183
臂展 169 167 173 172 173 170 177 174 176 185
b.20名男生臂展与身高数据的平均数、中位数、众数如下表:
平均数 中位数 众数
身高 175 m 173
臂展 170 169
c.20名男生臂展的频数分布直方图如图①:(将臂展数据分成5组:,)
d.20名男生臂展与身高的散点图如图②,活动小组发现图中大部分点落在一条直线附近的狭长带形区域内.他们利用计算机和简单统计软件得到了描述臂展与身高之间关联关系的直线.
根据以上信息,回答下列问题:
(1)写出表中、的值: , ;
(2)该校九年级有男生240人,估计其中臂展大于或等于的男生人数;
(3)图②中直线近似的函数关系式为,根据直线反映的趋势,估计身高为男生的臂展长度.
21.随着我国人工智能科技的快速发展,智能机器人已经走进我们的生活.某快递公司使用甲、乙两台不同型号的智能机器人进行快递分拣工作,它们工作时各自的速度均保持不变.已知某天它们同时开始工作,甲机器人工作一段时间后、停工保养.保养结束后又和乙机器人一起继续工作.甲、乙两台机器人分拣快递的总数量(件)与乙机器人工作时间(分钟)之间的函数关系如图所示.
(1)甲机器人停工保养的时间为 分钟, ;
(2)求所在直线对应的函数表达式;
(3)若该快递公司当天分拣快递的总数批为5450件,则乙机器人工作时间为 分钟.
22.数学活动:探究平面图形的最小覆盖圆
【定义】我们称能完全覆盖某平面图形的圆(即该平面图形上所有的点均在圆内或圆上)为该平面图形的覆盖圆.其中,能完全覆盖平面图形的最小的圆(即直径最小)称为该平面图形的最小覆盖圆.
【探究一】线段的最小覆盖圆
线段的覆盖圆有无数个,其中,以为直径的圆是其最小覆盖圆.
理由如下:易知线段的最小覆盖圆一定经过点、点.如图①,以为直径作,再过、两点作(与不重合),连结.在中,有().
,
,即的直径大于的直径.
是线段的最小覆盖圆.“”处应填写的推理依据为 .
【探究二】直角三角形的最小覆盖圆
要确定直角三角形的最小覆盖圆,我们可先将其转化为【探究一】中线段的最小覆盖圆问题.这样就可以先确定直角三角形最长边(斜边)的最小覆盖圆,再判断直角顶点与这个圆的位置关系,从而确定直角三角形的最小覆盖圆.如图②,在中,.是以为直径的圆.请你判断点与的位置关系,并说明理由.
又由【探究一】可知,是最长边的最小覆盖圆,所以,是的最小覆盖圆.
【拓展应用】矩形的最小覆盖圆
如图③,在矩形中,,.
(1)用圆规和无刻度的直尺在图③中作矩形的最小覆盖圆:(不写做法,保留作图痕迹,作图确定后必须用黑色字迹的签字笔描点)
(2)该矩形的最小覆盖圆的直径为 ;
(3)若用两个等圆完全覆盖矩形.则这样的两个等圆的最小直径为 .
23.如图,在中,,,点为边的中点,点为边上一动点,连接.将线段绕点顺时针旋转得到线段.
(1)线段的长为 ;
(2)当时,求的长;
(3)当点在边上时,求证:;
(4)当点到的距离是点到距离的2倍时,直接写出的长.
24.在平面直角坐标系中,点为坐标原点,抛物线经过点.点、是该抛物线上的两点,横坐标分别为、,已知点,作点关于点的对称点,作点关于点的对称点,构造四边形.
(1)求该抛物线所对应的函数表达式;
(2)当两点关于该抛物线的对称轴对称时,求点的坐标;
(3)设抛物线在、两点之间的部分(含、两点)为图象.当时,若图象的最高点与最低点的纵坐标之差为.求的值;
(4)连结、,当时,直接写出的取值范围(这里、、均是大于且小于的角).
参考答案
题号 1 2 3 4 5 6 7 8
答案 B C A B B A D C
9.2
10.(答案不唯一)
11.3
12.
13.
14.①②④
15.,4
16.
17.见解析
证明:∵,
∴,,
∴,
∴,
∴,
∵四边形是平行四边形,
∴四边形是菱形.
18.小林跑步的平均速度为4米每秒
解:设小林跑步的平均速度为米每秒,则小吉的平均速度为米每秒,
由题意得:,
解得:,
经检验,是原方程的解,且符合题意,
∴原方程的解为:,
答:小林跑步的平均速度为4米每秒.
19.(1)见解析
(2)见解析
(3)见解析
(1)解:如图所示,即为所求;
(2)解;如图所示,即为所求;
(3)解:如图所示,即为所求.
20.(1);
(2)人
(3)身高为男生的臂展长度约为.
(1)解:由表格信息可得:;
;
(2)解:该校九年级有男生240人,估计臂展大于或等于170cm的男生人数为:
(人);
(3)解:∵,
当时,,
∴身高为男生的臂展长度约为.
21.(1),
(2)
(3)该快递公司当天分拣快递的总数批为5450件,则乙机器人工作时间为分钟.
(1)解:由图象可得:甲机器人停工保养的时间为分钟;
∵,
∴(件);
(2)解:∵甲乙机器人的效率为每分钟件,
∴所在直线对应的函数表达式为:;
(3)解:当时,
∴,
解得:,
∴该快递公司当天分拣快递的总数批为5450件,则乙机器人工作时间为分钟.
22.探究一:三角形的任意两边之和大于第三边;探究二:在上;证明见解析;拓展应用:(1)作图见解析;(2);(3);
解:探究一:
理由如下:易知线段的最小覆盖圆一定经过点、点.如图①,以为直径作,再过、两点作(与不重合),连结.在中,有(三角形的任意两边之和大于第三边).
,
,即的直径大于的直径.
是线段的最小覆盖圆.“”处应填写的推理依据为三角形的任意两边之和大于第三边.
故答案为:三角形的任意两边之和大于第三边;
探究二:∵,为的中点,
∴,
∴在上;
拓展应用:(1)如图,即为矩形的最小覆盖圆;
(2)∵矩形,,,
∴,;
(3)作的垂直平分线,交于,交于,
∴四边形,是两个全等的矩形,
∴,
∵用两个等圆完全覆盖矩形,
∴两圆一定过,
连接,交点分别为,
同理可得:这样的两个等圆的最小直径为或或或,
∴最小直径为,
如图,作的垂直平分线交于,
同法作,,此时不是直径最小的等圆;
综上:用两个等圆完全覆盖矩形.则这样的两个等圆的最小直径为.
23.(1)
(2)
(3)证明见解析
(4)的长为或.
(1)解:∵在中,,,
∴;
(2)解:如图,在中,,,点为边的中点,
∴,,
∵,
∴,而,
∴,
∴;
(3)证明:∵旋转,
∴,
如图,∵,,
∴,
∵,,
∴;
(4)解:如图,当在的左边时,结合题意可得:,,,
过作于,过作于,
∴四边形为矩形,
∴,
结合(1)可得:,
∵,,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴;
如图,当在的右边时,过作于,过作于,
同理:,
四边形四边形为矩形,
∴,
∵,
∴,
∴,,
同理可得:,,
∴;
综上:的长为或.
24.(1)
(2)
(3)或
(4)
(1)将点代入中得:
解得:,
∴.
(2)根据抛物线对称轴公式可知:
抛物线的对称轴为,
∵、关于对称轴对称,且横坐标分别为、,
∴、中点在对称轴上,
∴,
,
解得:,
∵点是该抛物线上的点,
将代入抛物线解析式得,
,
即
设是A关于的对称点,则:
解得,,
∴点坐标为.
(3)∵抛物线顶点为,开口向上,,,
当时,包含,最低点为。
当时,,最高点为A,纵坐标差为:,
解得:;
当时,,最高点为B,纵坐标差为: ,
解得:.
综上,m的值为或.
(4)∵点是点关于点的对称点,点是点关于点的对称点,结合题意可知:
∴,,,,
∴,,,,
当、运动到平行四边形内部时(即、、共线),如图:
过点作,如图:
此时,满足,
由一次函数的性质可的大小决定了直线的倾斜方向和函数的增减性,
所以当两条一次函数的直线平行时的大小相同,
∴
∴
解得
当、、共线时,如图,同理:
∴,
∴,
∴,
解得.
综上,.
同课章节目录
