初中数学沪科版八年级下册19.1 多边形的内角和 课件(24张PPT)
文档属性
| 名称 | 初中数学沪科版八年级下册19.1 多边形的内角和 课件(24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
19.1多边形的内角和
问题:在日常生活中,有哪些常见的多边形?
创设情境,导入新课
创设情境,导入新课
问题:在日常生活中,有哪些常见的多边形?
创设情境,导入新课
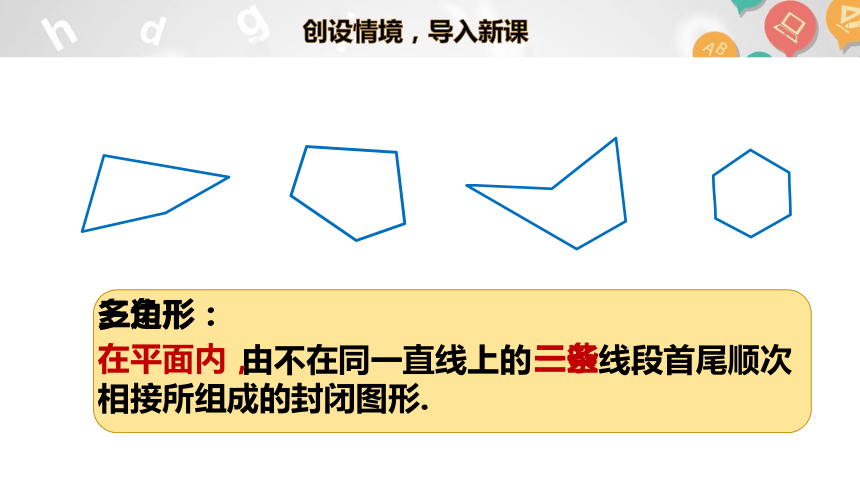
由不在同一直线上的 线段首尾顺次相接所组成的封闭图形.
三角形:
多边形:
一些
在平面内,
三条
创设情境,导入新课
多边形的相关概念
多边形的边:组成多边形的每一条线段
多边形的顶点:相邻的两条线段的公共端点
多边形的内角:多边形相邻两边所成的角
C
B
A
F
E
D
记作:六边形 ABCDEF
多边形的对角线:联结多边形的两个不相邻顶点的线段
师生互动,探索新知
A
B
C
D
E
A
B
C
D
E
师生互动,探索新知
A
B
C
D
E
A
B
C
D
E
否则叫做凹多边形.
对于一个多边形,画出它的任意一边所在的直线,如果其余各边都在这条直线的一侧,那么这个多边形叫凸多边形;
问题:这两个五边形有什么区别?
师生互动,探索新知
本章所讨论的多边形都是凸多边形.
A
B
C
D
问题:任意四边形内角和多少呢?为什么?
探究活动1:任意四边形的内角和.
师生互动,探索新知
探究活动2:n边形的内角和.
师生互动,探索新知
问题:任意n边形内角和是多少呢?为什么?
任务:完成表1并小组交流讨论各自选用的方法.
A1
A5
A4
A3
A2
An
n
A1
A5
A4
A3
A2
An
n
A5
A4
A3
A2
An
A1
n
A1
A5
A4
A3
A2
An
n
n边形内角和
若干个三角形内角和
转化
未知
已知
转化
解决
师生互动,探索新知
······
1
2
3
4
n -2
( n -2 )·180
1×180 =180
2×180 =360
3×180 =540
4×180 =720
······
······
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
图形
边数
······
师生互动,探索新知
探究活动2:n边形的内角和.
思考:
多边形的内角和等于 (n-2)·180°
.(n为不小于3的整数)
多边形内角和定理 :
师生互动,探索新知
n 边形内角和公式能解决哪些问题?
例题变式,内化新知
例:求八边形的内角和的度数。
解:(n-2)×180°=(8-2)×180°
=1080°
答:八边形的内角和为1080°。
例题变式,内化新知
变式1: 一个多边形的内角和是1440°,求这个多边形的边数.
设n为多边形的边数,则多边形的内角和为:
(n-2) ×180°(n大于等于3且n为整数),
由题意得:(n-2) ×180°= 1440°.
∴n=10
故这个多边形的边数为10.
例题变式,内化新知
变式2:八边形的内角和为 ,九边形的内角和为 。如果一个n边形的边数增加1,那么他的内角和增加 ,如果n边形的边数增加到原来的2倍,则内角和增加多少度?
1080°
1260°
180°
180°·n
课后思考 强化新知
思考题:有一张长方形的桌面,现在锯掉它的一个角,剩下的桌面是一个几边形?它的内角和是多少?
A
B
C
D
1. 本节课学习了哪些主要内容?
2. 在探究多边形内角和公式的过程中,你觉得有哪些
重要的方法?
3. 还有什么收获和疑问
反思总结,升华新知
19.1多边形的内角和
问题:在日常生活中,有哪些常见的多边形?
创设情境,导入新课
创设情境,导入新课
问题:在日常生活中,有哪些常见的多边形?
创设情境,导入新课
由不在同一直线上的 线段首尾顺次相接所组成的封闭图形.
三角形:
多边形:
一些
在平面内,
三条
创设情境,导入新课
多边形的相关概念
多边形的边:组成多边形的每一条线段
多边形的顶点:相邻的两条线段的公共端点
多边形的内角:多边形相邻两边所成的角
C
B
A
F
E
D
记作:六边形 ABCDEF
多边形的对角线:联结多边形的两个不相邻顶点的线段
师生互动,探索新知
A
B
C
D
E
A
B
C
D
E
师生互动,探索新知
A
B
C
D
E
A
B
C
D
E
否则叫做凹多边形.
对于一个多边形,画出它的任意一边所在的直线,如果其余各边都在这条直线的一侧,那么这个多边形叫凸多边形;
问题:这两个五边形有什么区别?
师生互动,探索新知
本章所讨论的多边形都是凸多边形.
A
B
C
D
问题:任意四边形内角和多少呢?为什么?
探究活动1:任意四边形的内角和.
师生互动,探索新知
探究活动2:n边形的内角和.
师生互动,探索新知
问题:任意n边形内角和是多少呢?为什么?
任务:完成表1并小组交流讨论各自选用的方法.
A1
A5
A4
A3
A2
An
n
A1
A5
A4
A3
A2
An
n
A5
A4
A3
A2
An
A1
n
A1
A5
A4
A3
A2
An
n
n边形内角和
若干个三角形内角和
转化
未知
已知
转化
解决
师生互动,探索新知
······
1
2
3
4
n -2
( n -2 )·180
1×180 =180
2×180 =360
3×180 =540
4×180 =720
······
······
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
图形
边数
······
师生互动,探索新知
探究活动2:n边形的内角和.
思考:
多边形的内角和等于 (n-2)·180°
.(n为不小于3的整数)
多边形内角和定理 :
师生互动,探索新知
n 边形内角和公式能解决哪些问题?
例题变式,内化新知
例:求八边形的内角和的度数。
解:(n-2)×180°=(8-2)×180°
=1080°
答:八边形的内角和为1080°。
例题变式,内化新知
变式1: 一个多边形的内角和是1440°,求这个多边形的边数.
设n为多边形的边数,则多边形的内角和为:
(n-2) ×180°(n大于等于3且n为整数),
由题意得:(n-2) ×180°= 1440°.
∴n=10
故这个多边形的边数为10.
例题变式,内化新知
变式2:八边形的内角和为 ,九边形的内角和为 。如果一个n边形的边数增加1,那么他的内角和增加 ,如果n边形的边数增加到原来的2倍,则内角和增加多少度?
1080°
1260°
180°
180°·n
课后思考 强化新知
思考题:有一张长方形的桌面,现在锯掉它的一个角,剩下的桌面是一个几边形?它的内角和是多少?
A
B
C
D
1. 本节课学习了哪些主要内容?
2. 在探究多边形内角和公式的过程中,你觉得有哪些
重要的方法?
3. 还有什么收获和疑问
反思总结,升华新知
