23.1.2 第2课时 互余两角的三角函数值 课件(共17张PPT) 沪科版(2024)数学九年级上册
文档属性
| 名称 | 23.1.2 第2课时 互余两角的三角函数值 课件(共17张PPT) 沪科版(2024)数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-08 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第23章 解直角三角形
23.1 锐角的三角函数
2. 30°,45°,60° 角的三角函数值
第2课时 互余两角的三角函数
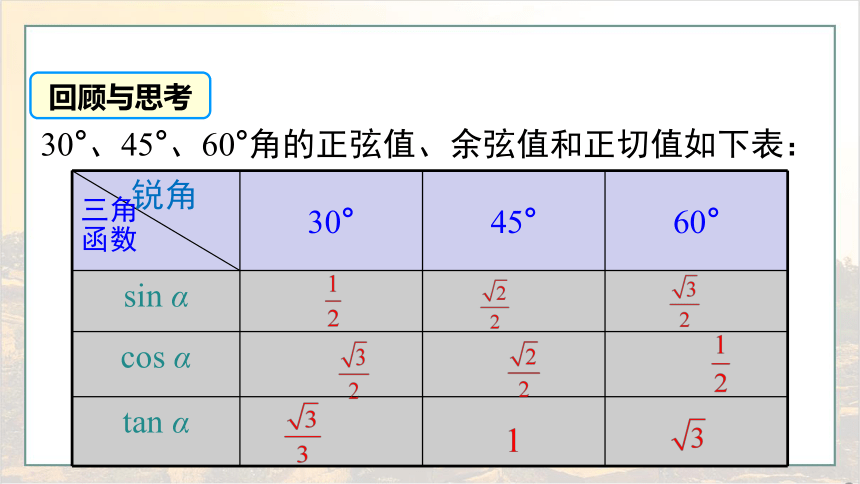
回顾与思考
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角 三角 函数 30° 45° 60°
sin α
cos α
tan α
从上面的练习中我们不难发现:
你还能从中发现什么规律呢?
sin 30° = cos 60°
sin 60° = cos 30°
sin 45° = cos 45°
规律:这些角的正(余)弦的值,分别等于它们余角的余(正)弦值.
问题 这个规律是否适合任意一个锐角呢?你能够用所学的知识证明你的结论吗?
提示:使用三角函数的定义证明.
A
C
B
c
a
b
互余两角的正弦、余弦值的关系
问题引导
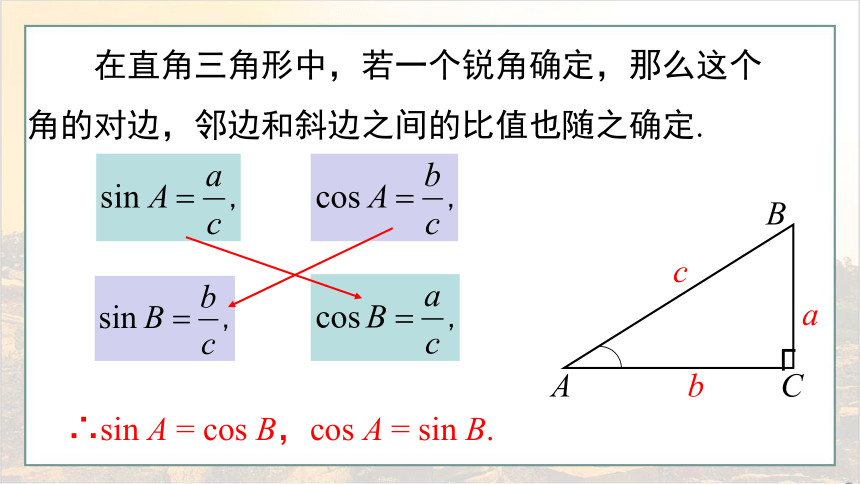
在直角三角形中,若一个锐角确定,那么这个角的对边,邻边和斜边之间的比值也随之确定.
b
A
B
C
a
┌
c
∴sin A = cos B,cos A = sin B.
∴sin A = cos B,cos A = sin B.
∵∠A +∠B = 90°,
∴∠B = 90°-∠A,
即 sin A = cos B = cos(90°-∠A),
cos A = sin B = sin(90°-∠A).
试一试:你能用文字叙述你发现的结论吗?
b
A
B
C
a
┌
c
任意一个锐角的正(余)弦值,等于它的余角的余(正)弦值.
归纳总结
几何语言:
∵∠A +∠B = 90°,
∴sinA = cosB,cosA = sinB.
例1 如图,在 △ABC 中,∠C=90°,若 sin A= ,求 cos B 的值.
解析:利用互余两角的正弦和余弦之间的关系可快速帮助我们解决问题,但要注意的是该结果只对互余的两个角成立.
典例精析
解 ∵∠A+∠B = 90°,
∴cos B = cos(90° - ∠A) = sin A =
例2 已知 cos α= ,α+β=90°,则 cos β=( )
C
解析:∵cos α= ,α+β=90°,∴sin β=cos α= .设 β 是一个直角三角形中的锐角,且 sin β= ,
设 b=3k,c=5k,则另一直角边的长度为 a=4k,
∴cos β =
利用互为余角的锐角三角函数关系时,先判断两角关系,然后再寻求锐角三角函数之间的关系.将角放到直角三角形中,画出图形,根据图形设出比例式,表示出各边.
方法总结
下列式子中,不成立的是( )
A.sin 35° = cos 55°
B.sin 30°+ sin 45° = sin 75°
C. cos 30° = sin 60°
D.sin260° + cos260° = 1
B
练一练
互余两个锐角的正切值的关系
b
A
B
C
a
┌
c
在直角三角形中,若一个锐角确定,那么这个角的对边和邻边之间的比值也随之确定.
结论:互余两个锐角的正切值互为倒数.
例3 在△ABC中,∠A,∠B是锐角,tanA,tanB是方程 3x2-tx+3=0 的两个根,则∠C=________.
解析:∵tan A,tan B 为方程 3x2-tx+3=0 的两根,
∠A,∠B 是锐角.
∴tan A·tan B=1.
∴∠A+∠B=90°. ∴∠C=180°-∠A-∠B=90°.
90°
【方法总结】利用 tan A·tan(90°-∠A)=1,可得∠A 与∠B 之间的关系,从而求出∠C 的大小.
解:∵在△ABC 中,∠C = 90°,tan A = ,
∴ tan B = .
又∵ sin A = ,
∴ cos B = sin A = .
1.在 △ABC 中,∠C = 90°,tan A= ,sin A= ,
(1)求 tan B,cos B。(2)求cosA.
知识拓展:
同一个锐角的三角函数之间的关系:
1. cos2A + sin2A=1
2.tan A=sinA/cosA
2.计算:
tan 33° · tan 34° · tan 35° · tan 55° · tan 56° · tan 57°
解:原式 = (tan 33° · tan 57°)( tan 34° · tan 56°)
(tan 35° · tan 55°)
=1×1×1
=1
互余两角的
三角函数
任意一个锐角的正(余)弦值,等于
它的余角的余(正)弦值.
互余两个锐角的正切值互为倒数.
第23章 解直角三角形
23.1 锐角的三角函数
2. 30°,45°,60° 角的三角函数值
第2课时 互余两角的三角函数
回顾与思考
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角 三角 函数 30° 45° 60°
sin α
cos α
tan α
从上面的练习中我们不难发现:
你还能从中发现什么规律呢?
sin 30° = cos 60°
sin 60° = cos 30°
sin 45° = cos 45°
规律:这些角的正(余)弦的值,分别等于它们余角的余(正)弦值.
问题 这个规律是否适合任意一个锐角呢?你能够用所学的知识证明你的结论吗?
提示:使用三角函数的定义证明.
A
C
B
c
a
b
互余两角的正弦、余弦值的关系
问题引导
在直角三角形中,若一个锐角确定,那么这个角的对边,邻边和斜边之间的比值也随之确定.
b
A
B
C
a
┌
c
∴sin A = cos B,cos A = sin B.
∴sin A = cos B,cos A = sin B.
∵∠A +∠B = 90°,
∴∠B = 90°-∠A,
即 sin A = cos B = cos(90°-∠A),
cos A = sin B = sin(90°-∠A).
试一试:你能用文字叙述你发现的结论吗?
b
A
B
C
a
┌
c
任意一个锐角的正(余)弦值,等于它的余角的余(正)弦值.
归纳总结
几何语言:
∵∠A +∠B = 90°,
∴sinA = cosB,cosA = sinB.
例1 如图,在 △ABC 中,∠C=90°,若 sin A= ,求 cos B 的值.
解析:利用互余两角的正弦和余弦之间的关系可快速帮助我们解决问题,但要注意的是该结果只对互余的两个角成立.
典例精析
解 ∵∠A+∠B = 90°,
∴cos B = cos(90° - ∠A) = sin A =
例2 已知 cos α= ,α+β=90°,则 cos β=( )
C
解析:∵cos α= ,α+β=90°,∴sin β=cos α= .设 β 是一个直角三角形中的锐角,且 sin β= ,
设 b=3k,c=5k,则另一直角边的长度为 a=4k,
∴cos β =
利用互为余角的锐角三角函数关系时,先判断两角关系,然后再寻求锐角三角函数之间的关系.将角放到直角三角形中,画出图形,根据图形设出比例式,表示出各边.
方法总结
下列式子中,不成立的是( )
A.sin 35° = cos 55°
B.sin 30°+ sin 45° = sin 75°
C. cos 30° = sin 60°
D.sin260° + cos260° = 1
B
练一练
互余两个锐角的正切值的关系
b
A
B
C
a
┌
c
在直角三角形中,若一个锐角确定,那么这个角的对边和邻边之间的比值也随之确定.
结论:互余两个锐角的正切值互为倒数.
例3 在△ABC中,∠A,∠B是锐角,tanA,tanB是方程 3x2-tx+3=0 的两个根,则∠C=________.
解析:∵tan A,tan B 为方程 3x2-tx+3=0 的两根,
∠A,∠B 是锐角.
∴tan A·tan B=1.
∴∠A+∠B=90°. ∴∠C=180°-∠A-∠B=90°.
90°
【方法总结】利用 tan A·tan(90°-∠A)=1,可得∠A 与∠B 之间的关系,从而求出∠C 的大小.
解:∵在△ABC 中,∠C = 90°,tan A = ,
∴ tan B = .
又∵ sin A = ,
∴ cos B = sin A = .
1.在 △ABC 中,∠C = 90°,tan A= ,sin A= ,
(1)求 tan B,cos B。(2)求cosA.
知识拓展:
同一个锐角的三角函数之间的关系:
1. cos2A + sin2A=1
2.tan A=sinA/cosA
2.计算:
tan 33° · tan 34° · tan 35° · tan 55° · tan 56° · tan 57°
解:原式 = (tan 33° · tan 57°)( tan 34° · tan 56°)
(tan 35° · tan 55°)
=1×1×1
=1
互余两角的
三角函数
任意一个锐角的正(余)弦值,等于
它的余角的余(正)弦值.
互余两个锐角的正切值互为倒数.
