14.1 全等三角形及其性质 课件(共28张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 14.1 全等三角形及其性质 课件(共28张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 22:40:38 | ||
图片预览




文档简介
(共28张PPT)
第14章 全等三角形
14.1 全等三角形及其性质
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
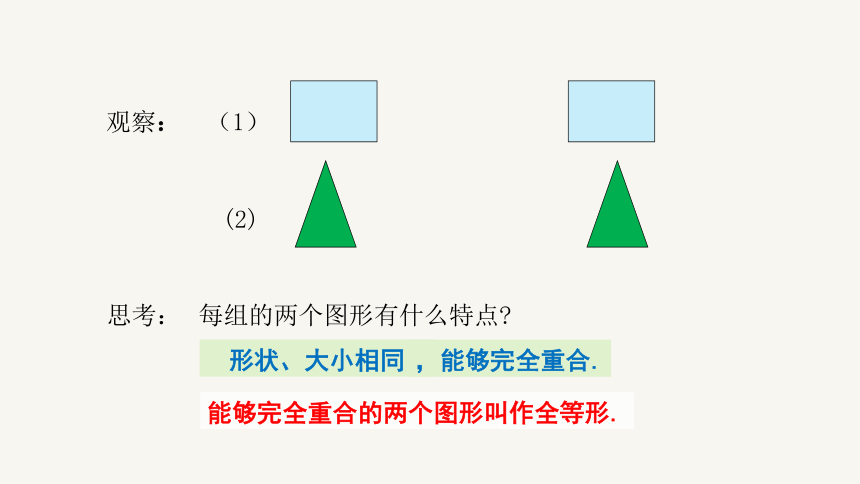
观察:
每组的两个图形有什么特点
思考:
(1)
(2)
能够完全重合的两个图形叫作全等形.
形状、大小相同
,能够完全重合.
新知初探
贰
新知初探
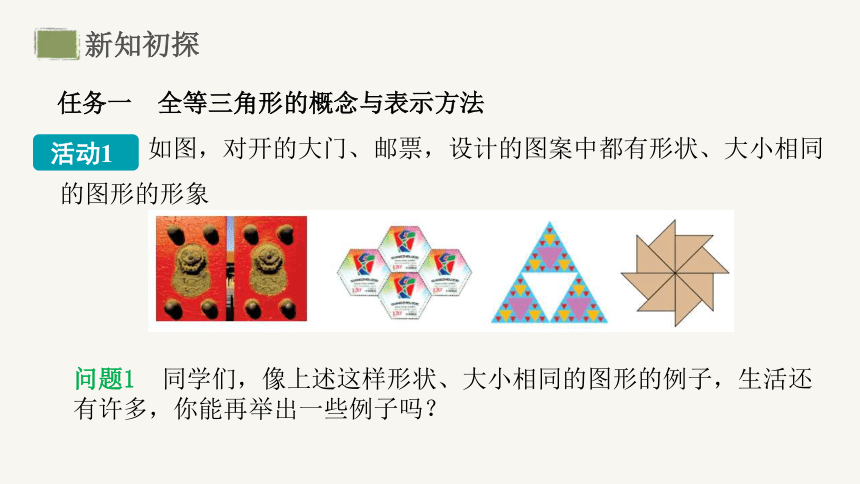
问题1 同学们,像上述这样形状、大小相同的图形的例子,生活还有许多,你能再举出一些例子吗?
任务一 全等三角形的概念与表示方法
如图,对开的大门、邮票,设计的图案中都有形状、大小相同的图形的形象
活动1
问题2 请同学们用复写纸画出两个三角形,并用剪刀剪下其中一个三角形,观察这两个三角形有何关系
能够完全重合的两个三角形叫作全等三角形.
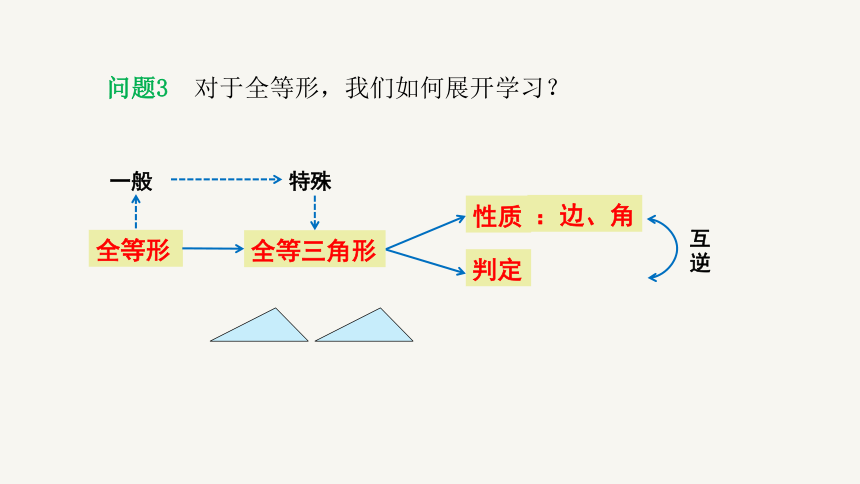
问题3 对于全等形,我们如何展开学习?
全等形
性质
判定
全等三角形
一般
特殊
:边、角
互逆
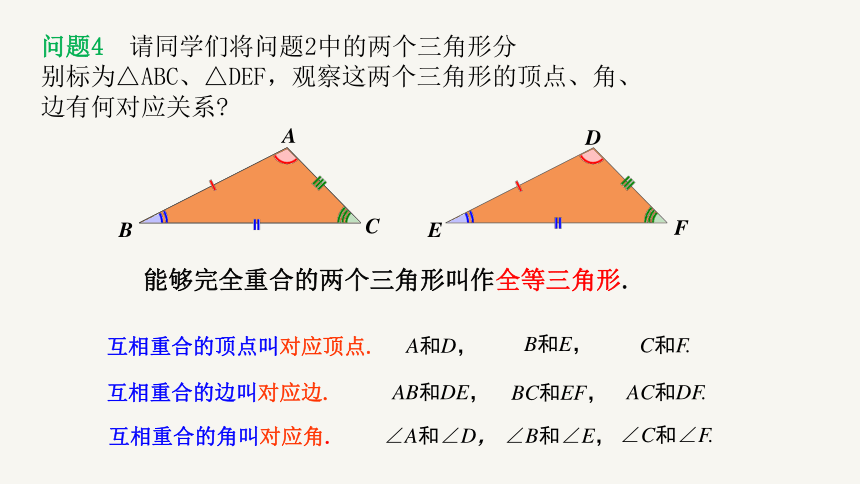
问题4 请同学们将问题2中的两个三角形分
别标为△ABC、△DEF,观察这两个三角形的顶点、角、
边有何对应关系
A
B
C
D
E
F
能够完全重合的两个三角形叫作全等三角形.
互相重合的顶点叫对应顶点.
互相重合的边叫对应边.
互相重合的角叫对应角.
A和D,
B和E,
C和F.
AB和DE,
BC和EF,
AC和DF.
∠A和∠D,
∠B和∠E,
∠C和∠F.
A
B
C
D
E
F
全等三角形及其有关概念
记作:△ABC≌△DEF
读作:△ABC全等于△DEF
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
“全等”用符号“≌”表示,读作“全等于”.
范例应用
【例1】 如图所示,△ABN≌△ACM,∠B、∠C是对应角,AB和AC是对应边,写出其他对应边及对应角.
解:对应边:AN和AM,BN和CM.
对应角:∠ANB和∠AMC,
∠NAB和∠MAC.
B
M
N
A
C
1、全等三角形中,公共边一定是对应边.
2、全等三角形中,公共角一定是对应角.
3、全等三角形中,对顶角一定是对应角.
4、全等三角形中,最长的边与最长的边是对应边,最短的边与最短的边是对应边,最大的角与最大的角是对应角,最小的角与最小的角是对应角.
5、对应角的对边为对应边,对应边的对角为对应角.
找对应边和对应角的方法
即时测评
如图所示,△AOC≌△BOD,C,D是对应点,下列结论错误的是( )
A.∠A与∠B是对应角
B.∠AOC与∠BOD是对应角
C.OC与OB是对应边
D.OC与OD是对应边
C
请同学们拿出准备好的三角形纸板,
按照课本P29图14.1.2把△ABC 进行平移、翻折或旋转,得到的新三角形与原三角形全等吗?
思考
将△ABC沿直线BC平移得到△DEF,两个三角形之间有什么关系?
1、△ABC与△DEF大小相等.
2、△ABC与△DEF形状相同.
3、△ABC与△DEF完全重合.
结论:一个图形经过平移后,位置发生变化,但是大小、形状没有发生变化,平移前后的两个图形是全等形.
A
C
B
D
F
E
平移
△ABC≌△DEF
活动2
思考
将△ABC沿直线BC翻折180°得到△DBC,两个三角形之间有什么关系?
1、△ABC与△DBC大小相等.
2、△ABC与△DBC形状相同.
3、△ABC与△DBC完全重合.
结论:一个图形经过翻折后,位置发生变化,但是大小、形状没有发生变化,翻折前后的两个图形是全等形.
A
C
B
D
翻折
△ABC≌△DBC
思考
将△ABC绕点A旋转,得到△ADE,两个三角形之间有什么关系?
1、△ABC与△ADE大小相等.
2、△ABC与△ADE形状相同.
3、△ABC与△ADE完全重合.
结论:一个图形经过旋转后,位置发生变化,但是大小、形状没有发生变化,旋转前后的两个图形是全等形.
A
C
B
D
E
旋转
△ABC≌△ADE
A
B
C
D
E
F
在平移三角形的过程中,△ABC≌△DEF,
对应边有什么关系?对应角呢?
性质:
全等三角形的对应边相等,对应角相等.
几何语言:
∵ △ABC≌△DEF,
∴ AB=DE,BC=EF,AC=DF,
∠A=∠D,∠B=∠E,∠C=∠F.
任务二 全等三角形的性质
活动1
范例应用
【例2】 已知△ABC≌△BAD,点A和点B,点C和点D是对应顶点,∠BAC=65°,∠ABC=26°,AC,BD的延长线相交于点E.求∠CBD,∠AEB的度数.
解:∵△ABC≌△BAD,
∴∠ABD=∠BAC=65°,
∴∠CBD=∠ABD-∠ABC=65°-26°=39°,
在△AEB中,∠AEB+∠BAE+∠ABE=180°,
∴∠AEB=180°-∠BAE-∠ABE=180°-65°-65°=50°.
即时测评
已知:如图,△ABC ≌△DEF.
(1)若DF =10 cm,则AC 的长为 ;
(2)若∠A =100°,则 ∠D 的度数为______.
A
B
C
D
E
F
10 cm
100°
10
10
100°
100°
已知:如图,△ABC ≌△DEF.
(3)若∠A =100°,∠B =30°,求∠F 的度数.
A
B
C
D
E
F
解:∵ ∠A =100°,∠B =30°,
∴ ∠C =180°-∠A -∠B
=180°-100°-30°
=50°.
∵ △ABC ≌△DEF,
∴ ∠F =∠C =50°.
100°
30°
50°
50°
当堂达标
叁
当堂达标
2.有下列说法: ①只有两个三角形才能完全重合; ②如果两个图形全等,那么它们的形状和大小一定都相同 ;③两个正方形一定是全等形;
④边数相同的图形一定能够重合. 其中错误说法的个数为( )
A.4 B.3 C.2 D.1
3.如图所示,△ABC≌△DEF,若∠A=100°,∠F=46°,则∠DEF等于( )A.100° B.54° C.46° D.34°
B
1.下列各组图形是全等形的是( )
D
D
4.如图所示,已知△ABD≌△ACD,且点B,D,C在同一条直线上,那么AD与BC有怎样的位置关系 为什么
解:AD⊥BC.理由:
∵△ABD≌△ACD,
∴∠ADB=∠ADC.
又∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°
∴AD⊥BC.
解:(1)因为△ABC≌△DEF,
所以∠D=∠A=30°,∠E=∠B=50°.
因为∠DFE+∠D+∠E=180°,
所以∠DFE=180°-∠D-∠E
=180°-30°-50°
=100°.
(2)因为△ABC≌△DEF,
所以BC=EF.
所以BC-CF=EF-CF,
即BF=EC.
因为BF=8,所以EC=8.
5.如图,△ABC≌△DEF,∠A=30°,∠B=50°,BF=8.
(1)求∠DFE的度数;
(2)求EC的长.
课堂小结
肆
课堂小结
全等形
全等三角形
性质
对应边相等,对应角相等.
判定
平移、翻折、旋转
课后作业
基础题:1.课后习题 第 1,2题。
提高题:2.请学有余力的同学完成课后习题第3题
谢
谢
第14章 全等三角形
14.1 全等三角形及其性质
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
观察:
每组的两个图形有什么特点
思考:
(1)
(2)
能够完全重合的两个图形叫作全等形.
形状、大小相同
,能够完全重合.
新知初探
贰
新知初探
问题1 同学们,像上述这样形状、大小相同的图形的例子,生活还有许多,你能再举出一些例子吗?
任务一 全等三角形的概念与表示方法
如图,对开的大门、邮票,设计的图案中都有形状、大小相同的图形的形象
活动1
问题2 请同学们用复写纸画出两个三角形,并用剪刀剪下其中一个三角形,观察这两个三角形有何关系
能够完全重合的两个三角形叫作全等三角形.
问题3 对于全等形,我们如何展开学习?
全等形
性质
判定
全等三角形
一般
特殊
:边、角
互逆
问题4 请同学们将问题2中的两个三角形分
别标为△ABC、△DEF,观察这两个三角形的顶点、角、
边有何对应关系
A
B
C
D
E
F
能够完全重合的两个三角形叫作全等三角形.
互相重合的顶点叫对应顶点.
互相重合的边叫对应边.
互相重合的角叫对应角.
A和D,
B和E,
C和F.
AB和DE,
BC和EF,
AC和DF.
∠A和∠D,
∠B和∠E,
∠C和∠F.
A
B
C
D
E
F
全等三角形及其有关概念
记作:△ABC≌△DEF
读作:△ABC全等于△DEF
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
“全等”用符号“≌”表示,读作“全等于”.
范例应用
【例1】 如图所示,△ABN≌△ACM,∠B、∠C是对应角,AB和AC是对应边,写出其他对应边及对应角.
解:对应边:AN和AM,BN和CM.
对应角:∠ANB和∠AMC,
∠NAB和∠MAC.
B
M
N
A
C
1、全等三角形中,公共边一定是对应边.
2、全等三角形中,公共角一定是对应角.
3、全等三角形中,对顶角一定是对应角.
4、全等三角形中,最长的边与最长的边是对应边,最短的边与最短的边是对应边,最大的角与最大的角是对应角,最小的角与最小的角是对应角.
5、对应角的对边为对应边,对应边的对角为对应角.
找对应边和对应角的方法
即时测评
如图所示,△AOC≌△BOD,C,D是对应点,下列结论错误的是( )
A.∠A与∠B是对应角
B.∠AOC与∠BOD是对应角
C.OC与OB是对应边
D.OC与OD是对应边
C
请同学们拿出准备好的三角形纸板,
按照课本P29图14.1.2把△ABC 进行平移、翻折或旋转,得到的新三角形与原三角形全等吗?
思考
将△ABC沿直线BC平移得到△DEF,两个三角形之间有什么关系?
1、△ABC与△DEF大小相等.
2、△ABC与△DEF形状相同.
3、△ABC与△DEF完全重合.
结论:一个图形经过平移后,位置发生变化,但是大小、形状没有发生变化,平移前后的两个图形是全等形.
A
C
B
D
F
E
平移
△ABC≌△DEF
活动2
思考
将△ABC沿直线BC翻折180°得到△DBC,两个三角形之间有什么关系?
1、△ABC与△DBC大小相等.
2、△ABC与△DBC形状相同.
3、△ABC与△DBC完全重合.
结论:一个图形经过翻折后,位置发生变化,但是大小、形状没有发生变化,翻折前后的两个图形是全等形.
A
C
B
D
翻折
△ABC≌△DBC
思考
将△ABC绕点A旋转,得到△ADE,两个三角形之间有什么关系?
1、△ABC与△ADE大小相等.
2、△ABC与△ADE形状相同.
3、△ABC与△ADE完全重合.
结论:一个图形经过旋转后,位置发生变化,但是大小、形状没有发生变化,旋转前后的两个图形是全等形.
A
C
B
D
E
旋转
△ABC≌△ADE
A
B
C
D
E
F
在平移三角形的过程中,△ABC≌△DEF,
对应边有什么关系?对应角呢?
性质:
全等三角形的对应边相等,对应角相等.
几何语言:
∵ △ABC≌△DEF,
∴ AB=DE,BC=EF,AC=DF,
∠A=∠D,∠B=∠E,∠C=∠F.
任务二 全等三角形的性质
活动1
范例应用
【例2】 已知△ABC≌△BAD,点A和点B,点C和点D是对应顶点,∠BAC=65°,∠ABC=26°,AC,BD的延长线相交于点E.求∠CBD,∠AEB的度数.
解:∵△ABC≌△BAD,
∴∠ABD=∠BAC=65°,
∴∠CBD=∠ABD-∠ABC=65°-26°=39°,
在△AEB中,∠AEB+∠BAE+∠ABE=180°,
∴∠AEB=180°-∠BAE-∠ABE=180°-65°-65°=50°.
即时测评
已知:如图,△ABC ≌△DEF.
(1)若DF =10 cm,则AC 的长为 ;
(2)若∠A =100°,则 ∠D 的度数为______.
A
B
C
D
E
F
10 cm
100°
10
10
100°
100°
已知:如图,△ABC ≌△DEF.
(3)若∠A =100°,∠B =30°,求∠F 的度数.
A
B
C
D
E
F
解:∵ ∠A =100°,∠B =30°,
∴ ∠C =180°-∠A -∠B
=180°-100°-30°
=50°.
∵ △ABC ≌△DEF,
∴ ∠F =∠C =50°.
100°
30°
50°
50°
当堂达标
叁
当堂达标
2.有下列说法: ①只有两个三角形才能完全重合; ②如果两个图形全等,那么它们的形状和大小一定都相同 ;③两个正方形一定是全等形;
④边数相同的图形一定能够重合. 其中错误说法的个数为( )
A.4 B.3 C.2 D.1
3.如图所示,△ABC≌△DEF,若∠A=100°,∠F=46°,则∠DEF等于( )A.100° B.54° C.46° D.34°
B
1.下列各组图形是全等形的是( )
D
D
4.如图所示,已知△ABD≌△ACD,且点B,D,C在同一条直线上,那么AD与BC有怎样的位置关系 为什么
解:AD⊥BC.理由:
∵△ABD≌△ACD,
∴∠ADB=∠ADC.
又∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°
∴AD⊥BC.
解:(1)因为△ABC≌△DEF,
所以∠D=∠A=30°,∠E=∠B=50°.
因为∠DFE+∠D+∠E=180°,
所以∠DFE=180°-∠D-∠E
=180°-30°-50°
=100°.
(2)因为△ABC≌△DEF,
所以BC=EF.
所以BC-CF=EF-CF,
即BF=EC.
因为BF=8,所以EC=8.
5.如图,△ABC≌△DEF,∠A=30°,∠B=50°,BF=8.
(1)求∠DFE的度数;
(2)求EC的长.
课堂小结
肆
课堂小结
全等形
全等三角形
性质
对应边相等,对应角相等.
判定
平移、翻折、旋转
课后作业
基础题:1.课后习题 第 1,2题。
提高题:2.请学有余力的同学完成课后习题第3题
谢
谢
同课章节目录
