14.2 三角形全等的判定 第1课时 SAS 课件(共24张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 14.2 三角形全等的判定 第1课时 SAS 课件(共24张PPT) 2025-2026学年数学人教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
第14章 全等三角形
4.2 三角形全等的判定
第1课时 SAS
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
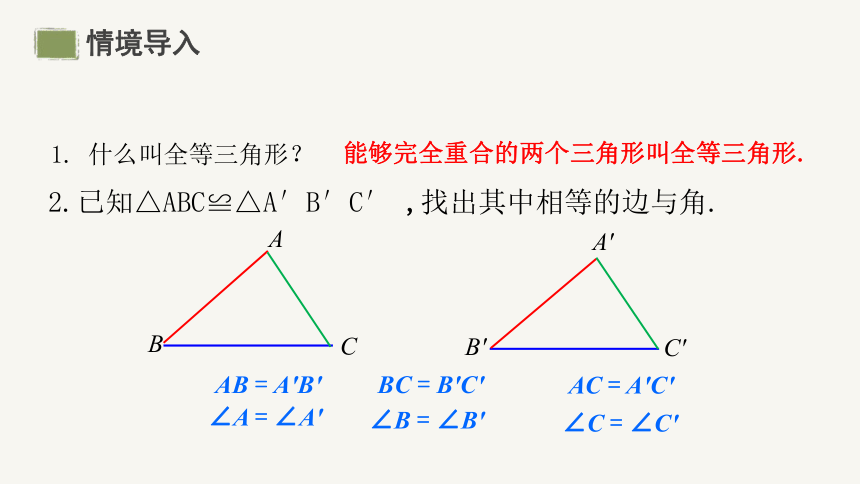
∠A = ∠A′
AB = A′B′
2.已知△ABC≌△A′B′C′ ,找出其中相等的边与角.
∠B = ∠B′
BC = B′C′
∠C = ∠C′
AC = A′C′
1. 什么叫全等三角形?
能够完全重合的两个三角形叫全等三角形.
A
B
C
A′
B′
C′
为了庆祝国庆节,老师要求同学们回家制作三角形彩旗(如图),那么,老师应提供多少个数据才能保证同学们制作出来的三角形彩旗全等呢?一定要知道所有的边长和所有的角度吗?
新知初探
贰
新知初探
任务一 探索全等三角形的判定方法
如果△ABC≌△A'B'C',则有对应边相等,对应角相等.反之,根据全等三角形的定义,如果满足三条边分别相等,三个角分别相等,那么△ABC和△A'B'C'能够完全重合,即判定△ABC≌△A'B'C'.
如果只选取其中的一部分条件还能保证两个三角形全等吗?
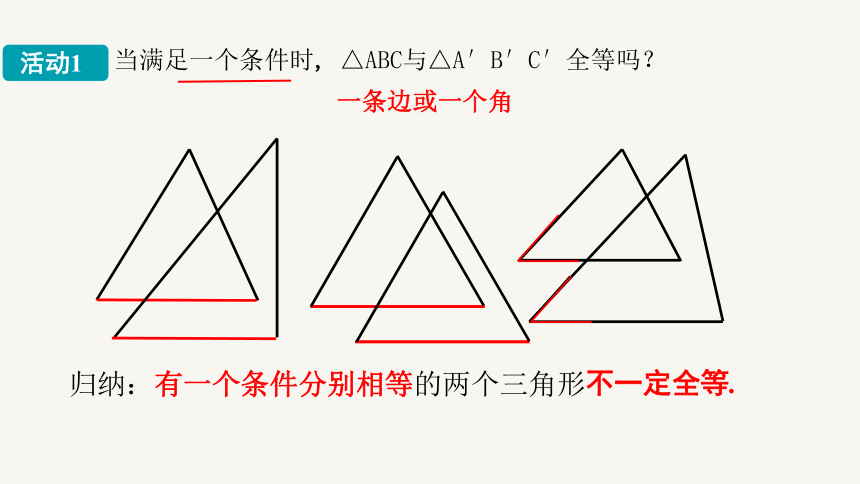
当满足一个条件时, △ABC与△A′B′C′全等吗?
一条边或一个角
归纳:有一个条件分别相等的两个三角形
不一定全等.
活动1
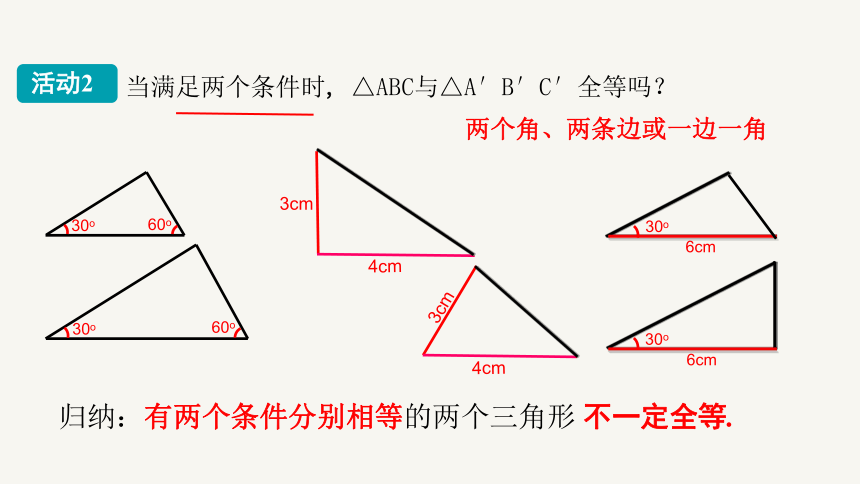
3cm
4cm
3cm
4cm
当满足两个条件时, △ABC与△A′B′C′全等吗?
两个角、两条边或一边一角
归纳:有两个条件分别相等的两个三角形
6cm
30o
30o
6cm
60o
30o
30o
60o
不一定全等.
活动2
当满足三个条件时, △ABC与△A′B′C′全等吗?
我们先研究两条边+一个角分别相等的情况
其他几种情况后续再进行研究.
三条边
三个角
两条边+一个角
两个角+一条边
活动3
任务二 边角边的判定方法
已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置上有几种可能性呢?
A
B
C
A
B
C
“两边及夹角”
“两边和其中一边的对角”
它们能判定两个三角形全等吗?
△ABC与△A'B'C'中,如果A'B'=AB,
∠A'=∠A,C'A'=CA,那么△ABC与△A'B'C'会全等吗?为什么?
A
B
C
A′
B′
C′
思考:
① △A′ B′ C′ 与 △ABC 全等吗?如何验证?
②这两个三角形全等是满足哪三个条件?
活动1
1.由∠A'=∠A可知,∠A'与∠A可以重合,即射线AC与射线A’C’重合,射线AB与射线A’B’重合,
2.由A'B'=AB,C'A'=CA,可知点B',C'分别与点B,C重合.
3.△ABC的三个顶点分别与△A'B'C'的三个顶点重合
△ABC≌△A'B'C'
文字语言:
两边和它们的夹角分别相等的两个三角形全等.
(简写成“边角边”或“SAS ”).
“边角边”判定方法
在△ABC 和△ DEF中,
∴ △ABC ≌△ DEF(SAS).
几何语言:
AB = DE,
∠A =∠D,
AC =AF ,
A
B
C
D
E
F
必须是两边“夹角”
范例应用
【例1】 如图,AC=AD,AB平分∠CAD,,求证:∠C=∠D.
证明:∵AB平分∠CAD,
∴∠CAB=∠DAB.
在△ABC 和△ABD中,
∴△ABC≌△ABD (SAS).
∴∠C=∠D.
如果把“两边及其夹角分别相等”
改为“两边及其中一边的对角相等”,那么这两个三角形还全等吗
如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
B
A
C
D
△ABC和△ABD满足AB=AB ,AC=AD,
∠B=∠B,但△ABC与△ABD不全等.
想一想
有两边和其中一边的对角分别相等的两个三角形不一定全等.
结论
活动2
即时测评
下列条件中,不能证明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
解析:要判断能不能使△ABC≌△DEF,应看所给出的条件是不是两边和这两边的夹角,只有选项C的条件不符合,故选C.
C
方法总结:判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.解题时要根据已知条件的位置来考虑,只具备SSA时是不能判定三角形全等的.
当堂达标
叁
1. 如图中的两个三角形全等的是( )
(A)③④ (B)②③ (C)①② (D)①④
当堂达标
C
2.如图所示,已知∠1=∠2,若用“SAS”证明
△ACB≌△BDA,还需加上条件( )
(A)BC=AD (B)AC=BD (C)∠C=∠D (D)OA=OB
B
3.如图,已知AB=BD,∠A=∠D,若直接应用“SAS”判定
△ABC≌△DBE,则需要添加的一个条件是 .
AC=DE
4.如图所示,AB = AC,AD = AE,∠BAC =∠DAE,
求证:△ABD ≌△ACE.
证明:因为∠BAC =∠DAE,
所以∠BAC+∠CAD =∠DAE +∠CAD,
即∠BAD =∠CAE,
在△ABD和△ACE中,
所以△ABD≌△ACE(SAS).
5.如图,把两根钢条AA',BB'的中点O连在一起,可以做成一个测量工件内槽宽的工具(工人把这种工具叫卡钳),只要量出A'B'的长度,就可以知道工件的内径AB是否符合标准,你能简要说出工人这样测量的道理吗
解:在△OAB和△OA'B'中,
∴△OAB≌△OA'B'(SAS).
∴AB=A'B'.
课堂小结
肆
课堂小结
一个判定
一种思想
三角形 全等
分类讨论
SAS
课后作业
基础题:1.课后习题 第 1,2题。
提高题:2.请学有余力的同学完成课后习题第14题
谢
谢
第14章 全等三角形
4.2 三角形全等的判定
第1课时 SAS
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
∠A = ∠A′
AB = A′B′
2.已知△ABC≌△A′B′C′ ,找出其中相等的边与角.
∠B = ∠B′
BC = B′C′
∠C = ∠C′
AC = A′C′
1. 什么叫全等三角形?
能够完全重合的两个三角形叫全等三角形.
A
B
C
A′
B′
C′
为了庆祝国庆节,老师要求同学们回家制作三角形彩旗(如图),那么,老师应提供多少个数据才能保证同学们制作出来的三角形彩旗全等呢?一定要知道所有的边长和所有的角度吗?
新知初探
贰
新知初探
任务一 探索全等三角形的判定方法
如果△ABC≌△A'B'C',则有对应边相等,对应角相等.反之,根据全等三角形的定义,如果满足三条边分别相等,三个角分别相等,那么△ABC和△A'B'C'能够完全重合,即判定△ABC≌△A'B'C'.
如果只选取其中的一部分条件还能保证两个三角形全等吗?
当满足一个条件时, △ABC与△A′B′C′全等吗?
一条边或一个角
归纳:有一个条件分别相等的两个三角形
不一定全等.
活动1
3cm
4cm
3cm
4cm
当满足两个条件时, △ABC与△A′B′C′全等吗?
两个角、两条边或一边一角
归纳:有两个条件分别相等的两个三角形
6cm
30o
30o
6cm
60o
30o
30o
60o
不一定全等.
活动2
当满足三个条件时, △ABC与△A′B′C′全等吗?
我们先研究两条边+一个角分别相等的情况
其他几种情况后续再进行研究.
三条边
三个角
两条边+一个角
两个角+一条边
活动3
任务二 边角边的判定方法
已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置上有几种可能性呢?
A
B
C
A
B
C
“两边及夹角”
“两边和其中一边的对角”
它们能判定两个三角形全等吗?
△ABC与△A'B'C'中,如果A'B'=AB,
∠A'=∠A,C'A'=CA,那么△ABC与△A'B'C'会全等吗?为什么?
A
B
C
A′
B′
C′
思考:
① △A′ B′ C′ 与 △ABC 全等吗?如何验证?
②这两个三角形全等是满足哪三个条件?
活动1
1.由∠A'=∠A可知,∠A'与∠A可以重合,即射线AC与射线A’C’重合,射线AB与射线A’B’重合,
2.由A'B'=AB,C'A'=CA,可知点B',C'分别与点B,C重合.
3.△ABC的三个顶点分别与△A'B'C'的三个顶点重合
△ABC≌△A'B'C'
文字语言:
两边和它们的夹角分别相等的两个三角形全等.
(简写成“边角边”或“SAS ”).
“边角边”判定方法
在△ABC 和△ DEF中,
∴ △ABC ≌△ DEF(SAS).
几何语言:
AB = DE,
∠A =∠D,
AC =AF ,
A
B
C
D
E
F
必须是两边“夹角”
范例应用
【例1】 如图,AC=AD,AB平分∠CAD,,求证:∠C=∠D.
证明:∵AB平分∠CAD,
∴∠CAB=∠DAB.
在△ABC 和△ABD中,
∴△ABC≌△ABD (SAS).
∴∠C=∠D.
如果把“两边及其夹角分别相等”
改为“两边及其中一边的对角相等”,那么这两个三角形还全等吗
如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
B
A
C
D
△ABC和△ABD满足AB=AB ,AC=AD,
∠B=∠B,但△ABC与△ABD不全等.
想一想
有两边和其中一边的对角分别相等的两个三角形不一定全等.
结论
活动2
即时测评
下列条件中,不能证明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
解析:要判断能不能使△ABC≌△DEF,应看所给出的条件是不是两边和这两边的夹角,只有选项C的条件不符合,故选C.
C
方法总结:判断三角形全等时,注意两边与其中一边的对角相等的两个三角形不一定全等.解题时要根据已知条件的位置来考虑,只具备SSA时是不能判定三角形全等的.
当堂达标
叁
1. 如图中的两个三角形全等的是( )
(A)③④ (B)②③ (C)①② (D)①④
当堂达标
C
2.如图所示,已知∠1=∠2,若用“SAS”证明
△ACB≌△BDA,还需加上条件( )
(A)BC=AD (B)AC=BD (C)∠C=∠D (D)OA=OB
B
3.如图,已知AB=BD,∠A=∠D,若直接应用“SAS”判定
△ABC≌△DBE,则需要添加的一个条件是 .
AC=DE
4.如图所示,AB = AC,AD = AE,∠BAC =∠DAE,
求证:△ABD ≌△ACE.
证明:因为∠BAC =∠DAE,
所以∠BAC+∠CAD =∠DAE +∠CAD,
即∠BAD =∠CAE,
在△ABD和△ACE中,
所以△ABD≌△ACE(SAS).
5.如图,把两根钢条AA',BB'的中点O连在一起,可以做成一个测量工件内槽宽的工具(工人把这种工具叫卡钳),只要量出A'B'的长度,就可以知道工件的内径AB是否符合标准,你能简要说出工人这样测量的道理吗
解:在△OAB和△OA'B'中,
∴△OAB≌△OA'B'(SAS).
∴AB=A'B'.
课堂小结
肆
课堂小结
一个判定
一种思想
三角形 全等
分类讨论
SAS
课后作业
基础题:1.课后习题 第 1,2题。
提高题:2.请学有余力的同学完成课后习题第14题
谢
谢
同课章节目录
