14.2 三角形全等的判定 第2课时 ASA和AAS 课件(共25张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 14.2 三角形全等的判定 第2课时 ASA和AAS 课件(共25张PPT) 2025-2026学年数学人教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-07 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
第14章 全等三角形
14.2 三角形全等的判定
第2课时 ASA和AAS
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
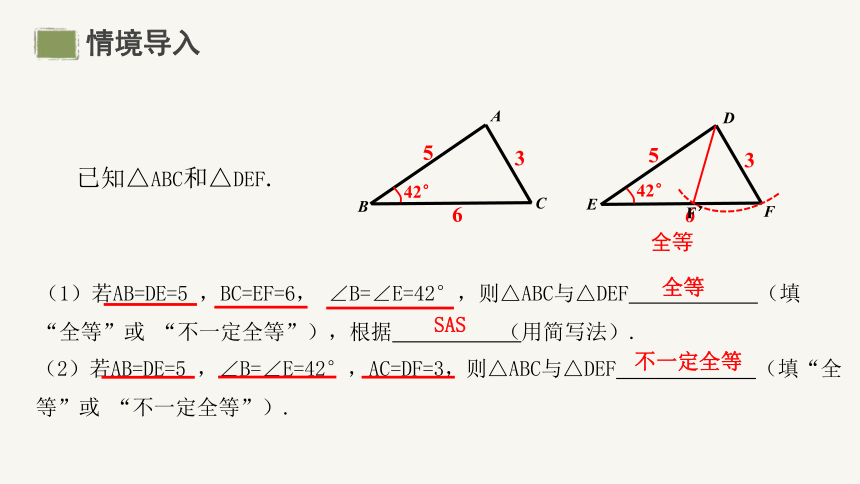
已知△ABC和△DEF.
B
C
D
E
F
(1)若AB=DE=5 ,BC=EF=6, ∠B=∠E=42°,则△ABC与△DEF (填“全等”或 “不一定全等”),根据 (用简写法).
A
(2)若AB=DE=5 ,∠B=∠E=42°,AC=DF=3,则△ABC与△DEF (填“全等”或 “不一定全等”).
5
5
3
3
6
6
全等
42°
42°
全等
SAS
不一定全等
F’
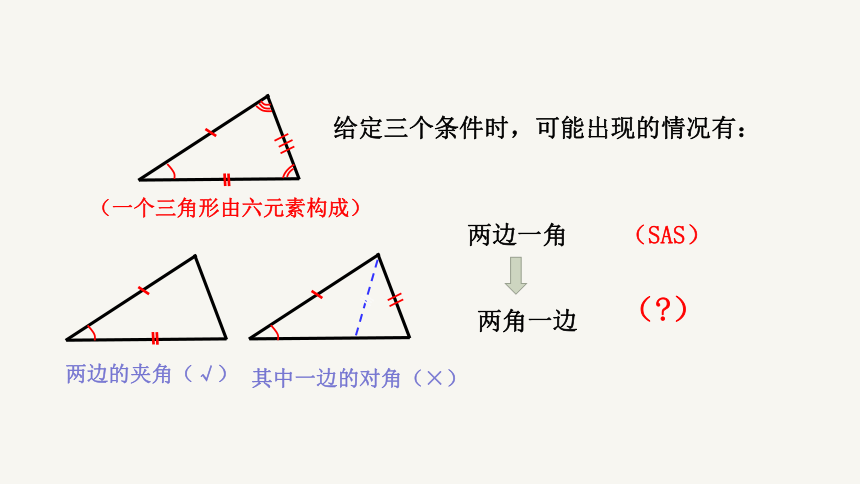
两边一角
给定三个条件时,可能出现的情况有:
两角一边
(SAS)
(一个三角形由六元素构成)
两边的夹角(√)
其中一边的对角(×)
( )
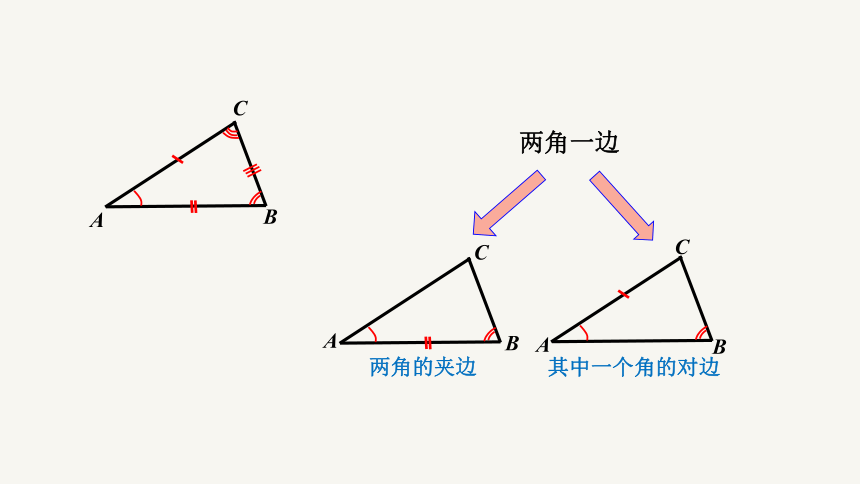
两角一边
两角的夹边
其中一个角的对边
C
B
A
C
B
A
C
B
A
新知初探
贰
新知初探
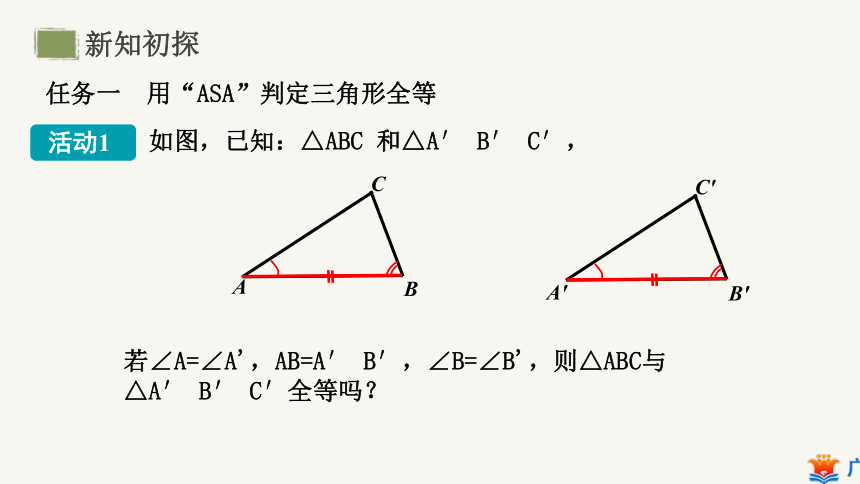
任务一 用“ASA”判定三角形全等
C
B
A
C'
B'
A'
如图,已知:△ABC 和△A′ B′ C′,
若∠A=∠A',AB=A′ B′,∠B=∠B',则△ABC与△A′ B′ C′全等吗?
活动1
C'
B'
A'
C
B
A
≌
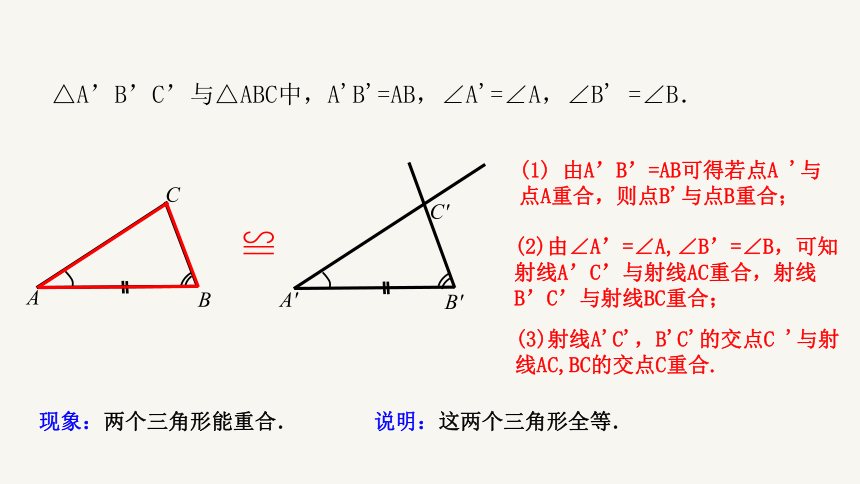
△A’B’C’与△ABC中,A'B'=AB,∠A'=∠A,∠B' =∠B.
(1) 由A’B’=AB可得若点A '与点A重合,则点B'与点B重合;
(2)由∠A’=∠A,∠B’=∠B,可知射线A’C’与射线AC重合,射线B’C’与射线BC重合;
现象:两个三角形能重合. 说明:这两个三角形全等.
(3)射线A'C',B'C'的交点C '与射线AC,BC的交点C重合.
两角和它们的夹边分别相等的两个三角形全等.
(简写为“角边角”或“ASA”)
C
B
A
C'
B'
A'
在△ABC和△A'B'C'中,
∴△ABC≌△ A'B'C' (ASA)
符号语言
图形语言
文字语言
归纳:
,
,
,
.
范例应用
【例1】 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.
求证:AD=AE.
题中有一隐含条件∠A既是△ACD的角,
又是△ABE的角——两个三角形的公共角.
分析:要证明AD=AE,只要证明△ACD≌△ABE
A
B
E
A
C
D
【例1】如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.
求证:AD=AE.
解答过程
证明:在△ACD和△ABE中,
∴△ACD≌△ABE(ASA).
∴AD=AE.
任务二 用“AAS”判定三角形全等
两角分别相等且其中一组等角的对边相等,这样的两个三角形全等吗
活动1
如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
要证△ABC≌△DEF,只需证∠C=∠F,利用“ASA”证明两个三角形全等.
分析:
证明:在△ABC中,∠A+∠B+∠C=180°,
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
∴∠C=180°-∠A-∠B.
同理 ∠F=180°-∠D-∠E.
又 ∠A=∠D , ∠B=∠E,
∴∠C=∠F.
解答过程
两角和其中一个角的对边分别相等的两个三角形全等.
(简写为“角角边”或“AAS”)
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS)
符号语言
文字语言
图形语言
归纳:
.
,
,
,
范例应用
【例2】如图,AD与BC相交于点O,且OA=OD,要添加一个条件,才能使得△AOB≌△DOC,那么,可以添加的一个条件是 ,
判断三角形全等的依据是 .
方法一:添加OB=OC(SAS)
方法二:添加∠A=∠D(ASA)
方法三:添加∠B=∠C(AAS)
当堂达标
叁
当堂达标
2.已知:如图,∠ABC=∠EBD,BC=BD,增加一个条件使得△ABC≌△EBD,下列条件中错误的是( )
A.AC=ED B.BA=BE
C.∠C=∠D D.∠A=∠E
1. 如图所示,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中,和△ABC全等的是( )
(A)只有乙 (B)只有丙 (C)乙和丙 (D)甲和乙
C
A
3.如图所示,∠ABC = ∠DEF,AB = DE,要证明△ABC ≌ △DEF,
(1)若以“SAS”为依据,还须添加的一个条件为____________.
(2)若以“ASA”为依据,还须添加的一个条件为_____________.
(3)若以“AAS”为依据,还须添加的一个条件为_____________.
BC = EF
∠A =∠D
∠ACB =∠F
4.如图所示,已知∠1=∠2,∠B=∠D,求证:△ABC≌△ADC.
1
2
A
B
D
C
5
6
所以△ABC ≌△ADC(AAS).
∠B=∠D,
∠5=∠6,
AC=AC,
在△ABC 和△ADC 中,
证明:因为∠1 是△ABC的外角,
∠2 是△ADC的外角,
所以∠5+∠B=∠1,
∠6+∠D=∠2.
因为∠B=∠D,∠1=∠2,
所以∠5=∠6.
5.如图,把一个长为10m的梯子AB斜靠在墙上,测得DM=8m,BM=6m,梯子沿墙下滑到CD位置,测得∠ABM=∠DCM,求梯子下滑的高度.
解:在△ABM与△DCM中,
∴△ABM≌△DCM(AAS),
∴BM=CM=6m,AM=DM=8m,
∴AC=AM-CM=2m.
即梯子下滑的高度是2m.
课堂小结
肆
课堂小结
1.本节课我们主要学习了哪些内容?
2.通过对两个三角形全等条件的进一步探究,你有什么收获?
(ASA、AAS)
(两边一角)
(两角一边)
(SAS)
(ASA、AAS)
全等
两个任意三角形
课后作业
基础题:1.课后习题 第 4,5题。
提高题:2.请学有余力的同学完成课后习题第15题
谢
谢
第14章 全等三角形
14.2 三角形全等的判定
第2课时 ASA和AAS
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
已知△ABC和△DEF.
B
C
D
E
F
(1)若AB=DE=5 ,BC=EF=6, ∠B=∠E=42°,则△ABC与△DEF (填“全等”或 “不一定全等”),根据 (用简写法).
A
(2)若AB=DE=5 ,∠B=∠E=42°,AC=DF=3,则△ABC与△DEF (填“全等”或 “不一定全等”).
5
5
3
3
6
6
全等
42°
42°
全等
SAS
不一定全等
F’
两边一角
给定三个条件时,可能出现的情况有:
两角一边
(SAS)
(一个三角形由六元素构成)
两边的夹角(√)
其中一边的对角(×)
( )
两角一边
两角的夹边
其中一个角的对边
C
B
A
C
B
A
C
B
A
新知初探
贰
新知初探
任务一 用“ASA”判定三角形全等
C
B
A
C'
B'
A'
如图,已知:△ABC 和△A′ B′ C′,
若∠A=∠A',AB=A′ B′,∠B=∠B',则△ABC与△A′ B′ C′全等吗?
活动1
C'
B'
A'
C
B
A
≌
△A’B’C’与△ABC中,A'B'=AB,∠A'=∠A,∠B' =∠B.
(1) 由A’B’=AB可得若点A '与点A重合,则点B'与点B重合;
(2)由∠A’=∠A,∠B’=∠B,可知射线A’C’与射线AC重合,射线B’C’与射线BC重合;
现象:两个三角形能重合. 说明:这两个三角形全等.
(3)射线A'C',B'C'的交点C '与射线AC,BC的交点C重合.
两角和它们的夹边分别相等的两个三角形全等.
(简写为“角边角”或“ASA”)
C
B
A
C'
B'
A'
在△ABC和△A'B'C'中,
∴△ABC≌△ A'B'C' (ASA)
符号语言
图形语言
文字语言
归纳:
,
,
,
.
范例应用
【例1】 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.
求证:AD=AE.
题中有一隐含条件∠A既是△ACD的角,
又是△ABE的角——两个三角形的公共角.
分析:要证明AD=AE,只要证明△ACD≌△ABE
A
B
E
A
C
D
【例1】如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.
求证:AD=AE.
解答过程
证明:在△ACD和△ABE中,
∴△ACD≌△ABE(ASA).
∴AD=AE.
任务二 用“AAS”判定三角形全等
两角分别相等且其中一组等角的对边相等,这样的两个三角形全等吗
活动1
如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
要证△ABC≌△DEF,只需证∠C=∠F,利用“ASA”证明两个三角形全等.
分析:
证明:在△ABC中,∠A+∠B+∠C=180°,
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
∴∠C=180°-∠A-∠B.
同理 ∠F=180°-∠D-∠E.
又 ∠A=∠D , ∠B=∠E,
∴∠C=∠F.
解答过程
两角和其中一个角的对边分别相等的两个三角形全等.
(简写为“角角边”或“AAS”)
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS)
符号语言
文字语言
图形语言
归纳:
.
,
,
,
范例应用
【例2】如图,AD与BC相交于点O,且OA=OD,要添加一个条件,才能使得△AOB≌△DOC,那么,可以添加的一个条件是 ,
判断三角形全等的依据是 .
方法一:添加OB=OC(SAS)
方法二:添加∠A=∠D(ASA)
方法三:添加∠B=∠C(AAS)
当堂达标
叁
当堂达标
2.已知:如图,∠ABC=∠EBD,BC=BD,增加一个条件使得△ABC≌△EBD,下列条件中错误的是( )
A.AC=ED B.BA=BE
C.∠C=∠D D.∠A=∠E
1. 如图所示,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中,和△ABC全等的是( )
(A)只有乙 (B)只有丙 (C)乙和丙 (D)甲和乙
C
A
3.如图所示,∠ABC = ∠DEF,AB = DE,要证明△ABC ≌ △DEF,
(1)若以“SAS”为依据,还须添加的一个条件为____________.
(2)若以“ASA”为依据,还须添加的一个条件为_____________.
(3)若以“AAS”为依据,还须添加的一个条件为_____________.
BC = EF
∠A =∠D
∠ACB =∠F
4.如图所示,已知∠1=∠2,∠B=∠D,求证:△ABC≌△ADC.
1
2
A
B
D
C
5
6
所以△ABC ≌△ADC(AAS).
∠B=∠D,
∠5=∠6,
AC=AC,
在△ABC 和△ADC 中,
证明:因为∠1 是△ABC的外角,
∠2 是△ADC的外角,
所以∠5+∠B=∠1,
∠6+∠D=∠2.
因为∠B=∠D,∠1=∠2,
所以∠5=∠6.
5.如图,把一个长为10m的梯子AB斜靠在墙上,测得DM=8m,BM=6m,梯子沿墙下滑到CD位置,测得∠ABM=∠DCM,求梯子下滑的高度.
解:在△ABM与△DCM中,
∴△ABM≌△DCM(AAS),
∴BM=CM=6m,AM=DM=8m,
∴AC=AM-CM=2m.
即梯子下滑的高度是2m.
课堂小结
肆
课堂小结
1.本节课我们主要学习了哪些内容?
2.通过对两个三角形全等条件的进一步探究,你有什么收获?
(ASA、AAS)
(两边一角)
(两角一边)
(SAS)
(ASA、AAS)
全等
两个任意三角形
课后作业
基础题:1.课后习题 第 4,5题。
提高题:2.请学有余力的同学完成课后习题第15题
谢
谢
同课章节目录
